均衡的概念#
在过去,你只要教会鹦鹉说「供给」与「需求」,那么这个世界就会多一位经济学家。多年后人们发现,要成为现代经济学家,这只鹦鹉必须再多学一个词,这个词就是「纳什均衡」。
均衡是博弈论的核心概念,它是参与人的最优策略的组合。在本部分,我们会通过具体的博弈例子介绍均衡的概念。在介绍之前,我们先简单思考一个问题,均衡存在吗? 下棋是博弈,下棋有最优策略吗?
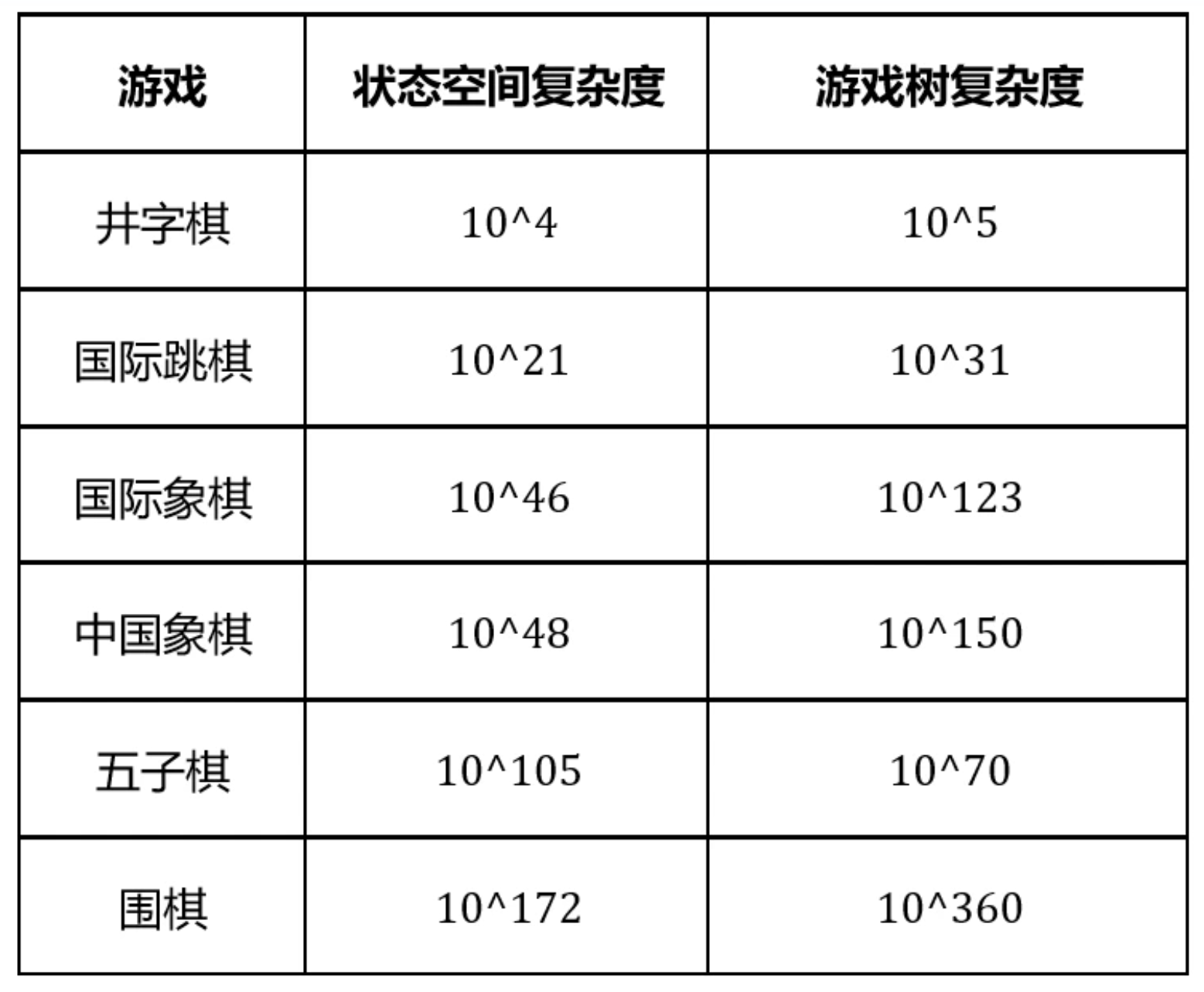
首先,我们来看井字棋。井字棋是一个简单的两人零和博弈,但它展示了博弈的复杂性。从状态复杂度来看,井字棋的每个格子有三种可能的状态:X、O或空,因此理论上可能的状态数为\(3^9\),即19683种。然而,这包括了不合规则、已结束以及对称重复的情况。当我们剔除这些无效状态后,实际的有效状态数会大大减少,大约为765种。
再来看博弈树的复杂度,它代表了博弈所有可能的路径。在井字棋中,第一步有9个格子可以选择,第二步有8个,以此类推。因此,博弈树复杂度的上限是\(9!\),即362880种可能。但同样地,我们需要剔除那些不符合规则、已结束或对称重复的走法,最终得到有效路径数约为26830种。
德国数学家策梅洛提出的策梅洛定理(Zermelo’s Theorem)指出,对于两人完全信息有限次博弈,如果满足以下四个条件:
有限性:博弈在有限步数内必然会结束。
完全信息:玩家对博弈状态完全了解。
无运气因素:结果仅取决于双方的选择。
轮流行动:玩家交替进行操作。
那么在博弈中,一定存在一个策略,要么先手一定获胜,要么后手一定获胜,要么双方一定平局。
因此根据策梅洛定理,对于井字棋这样的两人完全信息有限次博弈,其满足以上四个条件,所以一定存在确定的最优策略。现在我们已经知道井字棋的最优策略。如果双方都采用最优策略,游戏结果必然是平局。
接下来,我们转向围棋这一更为复杂的博弈。围棋的状态复杂度极高,达到\(3^{361}\),即约\(1.7 \times 10^{172}\)种可能的状态。而围棋的游戏树复杂度更是惊人,以平均每回合约250种合法走法、一局棋平均约150步来计算,其游戏树复杂度的下限已接近\(10^{360}\)。这意味着,即使我们拥有超级计算机,要计算出围棋的最优策略也需要极其漫长的时间,远远超出了我们的实际能力范围。所以虽然依据策梅洛定理,围棋存在最优策略,但是我们现在并未找到。尽管如此,我们仍然可以通过机器学习等方法来尝试找到更好的策略。
游戏 |
状态空间复杂度 |
游戏树复杂度 |
|---|---|---|
井字棋 |
10^4 |
10^5 |
国际跳棋 |
10^21 |
10^31 |
国际象棋 |
10^46 |
10^123 |
中国象棋 |
10^48 |
10^150 |
五子棋 |
10^105 |
10^70 |
围棋 |
10^172 |
10^360 |
check add table. 一些棋类游戏的状态空间和博弈树复杂度
在接下来的内容中,我们将通过一系列博弈介绍如何找出最优决策,和相应的均衡概念。
围棋的最优决策
尽管目前尚未找到围棋的最优策略,但机器学习技术的应用已显著提升了计算机在围棋比赛中的表现。最新的研究成果与算法,依托深度学习与强化学习的融合,以及GPU、TPU等硬件加速技术的助力,预示着未来围棋AI将更趋近甚至实现理论上的最优决策水平。
2015年,Google的DeepMind团队推出了AlphaGo,并随后发布了多个升级版本,如AlphaGo Lee、AlphaGo Master、AlphaGo Zero及AlphaZero,每一代都在前一代的基础上有所改进和创新。AlphaGo在其发展历程中战胜了多位围棋顶尖高手,包括在2015年8月以 5:0 的比分击败了三届欧洲冠军樊麾;2016年3月,AlphaGo更是在五番棋对决中以 4:1 的总比分战胜了世界冠军、韩国职业九段棋手李世石;在2016年末至2017年初,AlphaGo的升级版本Master在网上以「Master」的账号与中日韩三国的多位围棋高手进行了快棋对决,取得了60连胜的惊人战绩;2017年5月,在中国乌镇围棋峰会上,AlphaGo 与当时世界排名第一的中国围棋九段棋手柯洁进行了三番棋对决,并以3:0的总比分获胜。
一些机器学习算法:
AlphaZero:由DeepMind提出,它在围棋、国际象棋和将棋上均取得了卓越成绩。AlphaZero通过自我对弈来学习策略,并使用单一的神经网络同时预测策略和价值。这种方法使得AlphaZero不仅能够在围棋中表现出色,还能在其他游戏中展示出强大的学习能力。
MuZero:由DeepMind提出,它在AlphaZero的基础上进一步发展。MuZero的独特之处在于它能够在没有环境模型(即没有棋谱或奖励函数)的情况下学习棋类游戏(包括围棋)。MuZero展示了无需任何人类指导即可在多种环境中学习的强大能力。
Leela Zero:这是一个开源的围棋项目,它基于AlphaGo Zero的设计,但使用了不同的神经网络架构(如 ResNet)和优化器。Leela Zero通过社区的分布式计算资源进行自我对弈和训练。
KataGo:这是一个开源项目,专注于围棋的强化学习。它使用了类似AlphaZero的方法,并在某些方面进行了优化,使得它能够在相对较低的计算资源下达到高水平的性能。
囚徒博弈#
乙:坦白 |
乙:不坦白 |
|
|---|---|---|
甲:坦白 |
-10,-10 |
-1,-15 |
甲:不坦白 |
-15,-10 |
-2, -2 |
在囚徒困境中,嫌疑人甲和乙各自面临着两个选择:坦白或不坦白。然而,由于双方无法相互沟通,他们必须独立作出决定。从个体理性的角度来看,每个嫌疑人都会权衡自身的最大利益,具体分析如下:
如果对方坦白而我不坦白,我将面临更重的处罚;而如果选择坦白,那么对我来说至少不会比沉默更糟(因为处罚更轻)。所以,当对方坦白时,我应该选择坦白。
如果对方不坦白而我坦白,我将被判最轻的处罚;而如果不坦白,则处罚会比坦白更重。所以,当对方选择不坦白时,我也应该选择坦白。
综合上述分析,无论对方如何选择,坦白总是对我更有利的决策,因此我会选择坦白。
基于这种逻辑,每位嫌疑人都有动机选择坦白,从而使囚徒困境的均衡结果为(坦白,坦白)。在这种情况下,不论对方采取何种策略,参与者都会选择相同的策略,即「以不变应万变」。我们称这种策略为优势策略(dominant strategy),在本例中,坦白就是嫌疑人的优势策略。
优势策略:无论其他参与人采取什么策略,对于某个参与人来说,总有一个策略比其他任何策略都要好,或者至少一样好。如果参与人有优势策略,那么在理性决策的前提下,该参与人将始终采用这一策略。
优势策略均衡:如果所有参与人都有优势策略,那么由优势策略构成的均衡称为优势策略均衡。
进一步对比结果会发现,(坦白,坦白)的整体结果(两人都服刑十年)不如(不坦白,不坦白)(各服刑两年)来得有利。换言之,甲和乙整体最优(即帕累托最优)的结果是(不坦白,不坦白),这一结果帕累托优于(坦白,坦白)这一优势策略均衡。这表明,个人的最优选择不一定是集体的最优选择,对个人利益的追求未必能带来社会最优的结果 —— 纳什均衡不一定是社会最优解,这种情况被称为囚徒困境。
囚徒博弈展示了个体理性与集体理性之间的冲突。在博弈中,(不坦白,不坦白)代表了参与人合作的理想状态,而(坦白,坦白)则是不合作的选择。理论上,如果两名嫌疑人能够合作并且不坦白,他们将获得更轻的处罚。然而,由于缺乏信任和沟通机制,每位嫌疑人都出于自我保护的动机选择了坦白,从而导致了双输的局面。囚徒博弈揭示了在缺乏合作保证的情况下,个体理性如何可能导致非最优的集体结果。
为什么会出现个人理性和集体理性的冲突呢?关键在于理解「合作成本」的不可忽视性 – 个人和集体选择面对的局限条件是不同的。在囚徒博弈中,嫌犯间无法沟通的现实极大地提高了合作(即不坦白)的门槛,使得个人倾向于选择看似对自己更为安全的坦白策略。相比之下,集体视角则不考虑个体面临的实际限制,或者说是以一种上帝或全局视角来看待问题,这直接指向理论上的最优解(不坦白,不坦白)。因此,要调和这一冲突,关键在于降低合作的成本,如通过强化情感纽带(如兄弟情谊中的忠诚,不能背叛)、改变价值观念(如强调为他人付出的价值观)、调整激励机制或改变社会规范(如高额罚款以遏制不良行为或建立对背叛行为的严厉惩罚)或引入重复博弈机制(甲和乙不断进行囚徒博弈,利用长期互动中的信誉积累与惩罚措施促进合作)。这些都说明,通过改变参与者面对的约束条件,可以改变他们的选择。这也表明,在合作与竞争并存的社会环境中,如何建立有效的合作机制和信任基础至关重要。
智猪博弈#
假设在一个猪圈里有一只大猪和一只小猪。猪圈的一边有一个食槽,另一边有一个按钮。只有按下按钮,食槽里才会有食物。每次按下按钮会有8单位食物进入食槽,但这需要消耗相当于2单位食物的体力。如果大猪先到食槽边,它会吃掉7单位食物,小猪只能吃到1单位;如果小猪先到,它们各自吃4单位食物;如果它们同时到达,大猪吃5单位,小猪吃3单位。假设两只猪的跑步速度相同。两只猪可以选择按按钮或者在食槽边等待。因为这是一个同时行动的博弈,所以两只猪都有按按钮和等待这两个策略。其策略式如下表所示:
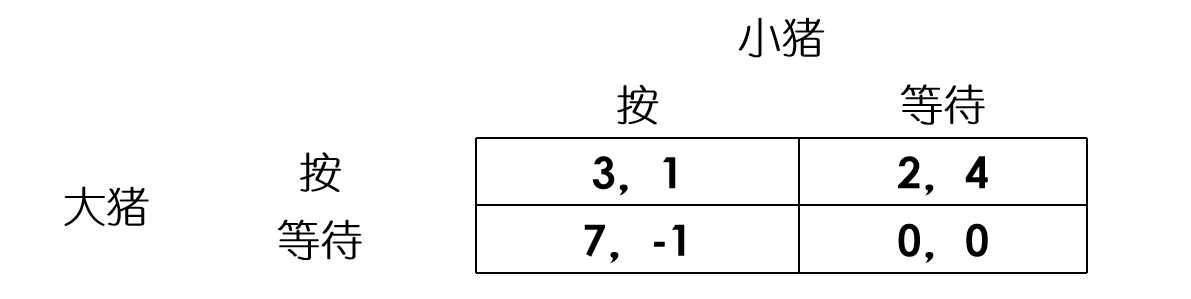
基于策略式,我们来分析一下两只猪的策略选择。先看小猪,当大猪选择按按钮时,小猪选择等待的收益更高。当大猪选择等待时,小猪同样选择等待的收益更高。因此,不论大猪选择什么,等待都是小猪的最佳选择或最佳对应。所以等待是小猪的优势策略。但对于大猪来说,当小猪选择按按钮时,大猪选择等待的收益最高;当小猪选择等待时,大猪选择等待的收益更高。大猪的最佳选择会随着小猪的选择而变化。因此,大猪没有优势策略,那我们应该如何思考这个博弈的均衡呢?
首先,等待是小猪的优势策略,所以小猪一定会选择等待。如果大猪能够分析出小猪的选择,它就会意识到,既然小猪不会选择按按钮,那它只需要考虑在小猪等待的情况下如何选择。当小猪选择等待时,大猪的最佳选择是按按钮。因此,博弈的均衡是(大猪选择按,小猪选择等待),简记为(按,等待)。
这里我们采用了换位思考的分析方式,先排除参与人肯定不会选择的策略,然后在剩下的策略中继续思考是否还能继续排除。如果最后只剩下一组策略组合,那么这就是博弈的均衡,称为重复剔除的优势策略均衡(Iterated Dominance Equilibrium)。
我们将参与者不会选择的策略称为劣势策略。寻找重复剔除的优势策略均衡的过程就是不断剔除劣势策略。
劣势策略:令 \(s_i'\) 和 \(s_i''\)是参与人i可选择的两个策略,如果对于任意的其他参与人的策略组合,参与人 \(i\)从选择 \(s_i''\)中得到的支付小于等于选择 \(s_i'\)得到的支付,则策略 \(s_i''\)是相对于\(s_i'\) 的劣势策略。
如果上述不等式严格成立,则称 \(s_i''\) 是相对于 \(s_i'\) 的严格劣势策略;如果不严格成立,则称 \(s_i''\) 是相对于 \(s_i'\) 的弱劣势策略。
显然,对于小猪,按按钮是相对于等待的劣势策略。将其剔除后,对于大猪,等待是相对于按按钮的劣势策略。再次剔除后,剩下的策略组合为(按,等待),这就是智猪博弈的重复剔除的优势均衡。
寻找重复剔除的优势策略均衡的方法
首先,找出某个参与人的劣势策略(假定存在),并将这个劣势策略剔除,重新构造一个不包含已剔除策略的新博弈;接着,在这个新博弈中再次剔除某个参与人的劣势策略;继续这个过程,直到只剩下一个唯一的策略组合为止。
如果这一过程不能继续,则不存在重复剔除的优势策略均衡。
数字博弈#
在这个博弈中,假设所有上微观经济学课程的同学作为博弈的参与者,每人需要从1到100中选择一个数字。最终,写出最接近所有人所选数字平均值的2/3的那个数字的同学将获得奖励。那么,这个博弈的均衡是什么呢?
首先,我们考虑最大的可能获胜数值,大家所选择的最大数字为100,100乘以2/3,即大约66.7。这说明均衡值的2/3是不可能超过66.7的,与之最接近的数字是67,说明68以上的数字不可能获胜,它们是相对于其它数字的劣势策略,我们可以排除68到100之间的数字,剔除之后,数字范围缩小为1-68。
接下来,我们按着同样的思路进行思考,考虑1到68这个缩小后的范围。这时,最大的可能获胜数值45 (\(68*2/3 \approx 45.3\))。因此,我们可以进一步排除46到68之间的数字。
再进一步,考虑1到45这个范围。最大的可能获胜数值是30 (\(45*2/3 = 30\))。因此,可以排除31到45之间的数字。
依此类推,重复剔除的过程一直持续,直到最终只剩下数字1,这时所有参与者的最优选择就是选择数字1,为重复剔除的优势策略均衡。
通过这个博弈,我们可以进一步理解在每一步剔除策略的过程中,对理性程度的加深。
在第一步中,之所以可以剔除68到100之间的数字,是因为参与者都是理性的,可以计算出最大可能得获胜数字为67。
在第二步中,之所以可以继续剔除46-68,需要参与人知道所有参与人都能够去进行第一步的思考,如果不行,那么则不能进行剔除。所以这里对理性的要求是,不仅所有参与者都是理性的,而且他们也知道所有参与人理性的,即 所有参与人知道所有参与人是理性的,这样才会再次调整自己的选择。
同理,在第三步中,之所以可以剔除,是因为参与人知道所有参与人都可以进行第二步的剔除,也就是要求,他们知道所有参与人知道所有参与人是理性的,即所有参与人知道所有参与人知道所有参与人是理性的。
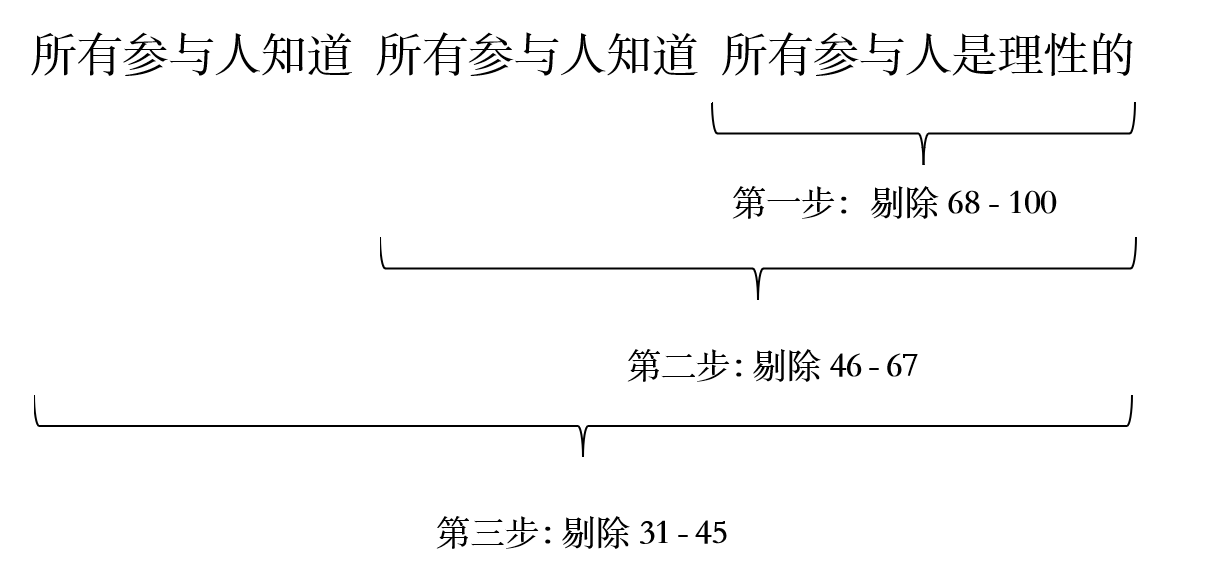
由此可见,每一步剔除都会对理性的要求加深一层。如果参与人的理性可以无限深入,就说理性是共同知识。
共同知识:群体中的所有人都知道某件事,而且他们都知晓其他人也知道这件事,如此反复……简单来说,就是所有人都知道,所有人都知道所有人都知道,以此类推。
由此可见,重复剔除的优势均衡的形成依赖于参与者之间的理性认识。如果理性不能层层递进,比如虽然所有参与者都是理性的,但他们不确定其他参与者是否同样理性,那么我们只能剔除第一步,而无法继续下去。这时,重复剔除的优势均衡就不再是有效预测参与者选择的方法。
胆小鬼博弈(斗鸡博弈)#
胆小鬼博弈描述了两辆车面对面高速驶来的情景。在这个情景中,谁先避让谁就会被视为“胆小鬼”(chicken),而另一位则被视为“勇敢者”,赢得这场较量。然而,如果双方都不避让,两车将会相撞,导致灾难性的后果,这显然是一个双输的局面。在现实中,如1962年古巴导弹危机期间的美苏对峙,就是胆小鬼博弈的一个例子。
1962年古巴导弹危机
1962年的古巴导弹危机是冷战期间美苏之间最紧张的一次直接对峙。在此之前,美国已经在土耳其部署了中程弹道导弹,作为回应,苏联开始在古巴秘密部署自己的导弹。当这些部署被美国侦察发现后,美国总统肯尼迪下令对古巴实施海上封锁,并要求苏联撤除其在古巴的导弹设施。在这场危机中,美国坚持要求苏联必须从古巴撤出所有进攻性武器,而苏联则坚称有权维护自己在古巴的军事存在,甚至暗示如果受到攻击可能会使用核武。
为了展示各自的决心并测试对方的决心,双方采取了一系列极具风险的边缘政策行动。美国不仅加强了军事集结,还对前往古巴的苏联船只进行了拦截。在一次特别危险的事件中,一艘苏联B-59号潜艇被美军驱逐舰包围,由于潜艇与莫斯科之间的通讯中断,艇长瓦列里·萨维茨基(Valery Savitsky)和他的船员们并不清楚地面上的局势。当美军驱逐舰投掷练习用手榴弹(实际上是信号弹或爆震装置),试图迫使潜艇浮出水面接受检查时,潜艇上的苏联军官误以为这是即将开战的信号。在这关键时刻,潜艇上的一位高级军官阿尔希波夫(Vasili Arkhipov)发挥了至关重要的作用。他坚持反对使用核鱼雷进行反击,并说服了其他两位指挥官不要采取行动,从而避免了一场可能升级为全面核战争的灾难。
尽管双方都不愿意主动退缩,但最终理智占据了上风。通过秘密外交渠道的谈判,美国总统肯尼迪与苏联领导人赫鲁晓夫达成了一项协议。根据这项协议,苏联同意撤除其在古巴的所有进攻性导弹,以换取美国承诺不入侵古巴。此外,美国还秘密地同意撤除之前部署在土耳其的导弹,从而缓解了苏联的安全顾虑。这场危机的成功解决避免了一场可能演变为全面核战争的灾难,也成为了国际关系史上通过外交途径化解重大危机的经典案例。
check add game
在这个博弈中,每个参与者的最优选择取决于对方的选择。例如,如果对方选择直行,我的最佳选择是避让;而如果对方选择避让,我的最佳选择则是直行。由于双方都没有优势策略或劣势策略,因此不存在优势策略均衡和重复剔除的优势策略均衡。那么,我们如何寻找均衡呢?
美国数学家约翰·纳什在20世纪50年代提出了一个重要的均衡概念,即纳什均衡。纳什均衡描述的是这样一种状态:在给定其他参与人选择不变的情况下,任何一位参与人都无法通过单方面改变自己的策略来提高收益。换句话说,在纳什均衡中,每个参与人的选择都是对其他参与人策略的最佳对应 (best response)。
纳什均衡:在一个策略组合中,如果在其他参与人都不改变已有策略的前提下,没有任何参与人有动力去改变自己的策略,那么这个策略组合就是一个纳什均衡。
为了找出纳什均衡,我们可以这样分析:在给定对手策略的情况下,标出每个参与人的最佳对应。具体来说,就是在参与人能够获得的最大支付下方画一条横线(划线法)。比如,在胆小鬼博弈中,当甲选择直行时,乙的最佳选择是避让(因为-1>-10),我们就在乙的支付-1下方画一条横线;当甲选择避让时,乙的最佳选择是直行(因为1>0),我们就在乙的支付0下方画一条横线。同样地,我们也为甲的最佳对应做上标记。
如{\numref}图%s<chicken>所示,,如果在某个策略组合里,所有参与人的支付都被标记上了横线,那么这个策略组合就是一个纳什均衡。就胆小鬼博弈而言,可以发现存在两个纳什均衡,分别是(甲避让,乙直行)和(甲直行,乙避让),这说明纳什均衡可能不是唯一的。
check add figure
优势策略均衡和重复剔除的优势均衡实际上是纳什均衡的特殊情况。纳什均衡意味着没有人愿意单方面改变自己的策略 —— 偏离现有策略不会增加他们的收益,也就是说参与人不会后悔他们的选择。例如,对于(直行,直行)这一策略组合,显然,如果一方知道另一方也选择直行,那么它会想要改选避让以减少损失(从-10提高到-1)。因此,(直行,直行)不是纳什均衡。相反,(避让,直行)这样的组合中,给定甲选择避让,乙没有动机偏离直行,因为那样只会使他的收益降低,所以(避让,直行)是纳什均衡。
显然,优势策略均衡和重复剔除的优势均衡都是纳什均衡的特殊情况。纳什均衡意味着无人愿变,没有参与人有单方面愿意改变策略的动力 —— 偏离不会使其收益严格增加,或者说参与人不后悔自己的选择。这可以作为判断一个策略组合是否是纳什均衡的标准。例如,对于(直行,直行)这一策略组合,显然给定对方的选择,参与人都有动力偏离选择避让,支付会由-10提高到-1。所以(直行,直行)不是纳什均衡。而对于(避让,直行),双方都没有动力–给定甲选择避让,乙偏离直行选择避让,支付会降低,因此(避让,直行)是纳什均衡。
纳什均衡也是一种自我实施的信念(self-fulfilling belief),如果所有人都预期并采纳纳什均衡,这个均衡便会自然形成。即使没有中央协调,也能达到某种形式的稳定状态。这有助于理解和预测现实世界中的许多互动现象,比如银行挤兑或时尚潮流的兴起。
石头-剪刀-布#
在石头-剪刀-布博弈中,如果使用划线法来标记每个参与人的最佳对应,我们会发现没有一个纯策略组合能够相互成为最佳对应。例如,当甲选择布时,乙的最佳选择是剪刀;而当乙选择剪刀时,甲的最佳选择又变成了石头;接着,当甲选择石头时,乙的最佳选择则变为布;如此循环往复。
根据纳什定理(1950),任何有限的博弈 —— 即参与人数量有限且每个参与人可选的纯策略集合也是有限的 —— 至少存在一个纳什均衡。显然,石头-剪刀-布是一个有限次博弈。那么,在这种情况下,如何找到纳什均衡呢?
如果我们考虑参与人可以依据一定的概率分布随机选择不同的策略,是否能找到相互为最佳对应的选择呢?假设甲以\(p_1\)、\(p_2\)、\(1-p_1-p_2\)的概率分别选择石头、布和剪刀;乙以\(q_1\)、\(q_2\)、\(1-q_1-q_2\)的概率分别选择石头、布和剪刀。给定乙的选择(\(q_1\),\(q_2\)),甲会调整\(p_1\)和\(p_2\)以最大化其期望支付:
通过一阶条件,我们可以得出:
从而得到,\(q_1 = q_2 = q_3 = 1/3\)。这意味着,当乙出剪刀、石头和布的概率相等时,甲无论选择哪种策略,其期望收益都是相同的。
若\(q_1 > 1/3\),即乙更有可能出石头时,甲以选择布(\(p_1 = 1\))的期望支付最高;若\(q_2 > 1/3\), 即乙更有可能出布时,甲选择剪刀(\(p_1=p_2= 0\))的期望支付最高;若\(1-q_1-q_2 > 1/3\),即乙更有可能出剪刀时, 甲出石头(\(p_1 = 1\))的期望支付最高。
同理,我们也可以计算出乙的最佳对应:
当甲以同样的概率选择石头、布和剪刀时,乙的期望收益同样不会因为改变策略而增加。
若 \(p_1 > 1/3\), 乙选择布(\(p_1 = 1\))。
若 \(p_2 > 1/3\), 乙选择剪刀(\(p_1=p_2= 0\))。
若 \(1-p_1-p_2 > 1/3\), 乙选择出石头。
当甲和乙都各自以 \(1/3\) 的概率选择石头、布和剪刀时,双方都没有动机偏离这一策略组合,因为此时任意一方都无法通过单方面改变策略来提高自己的期望支付。这就是该博弈的纳什均衡。
我们将参与人按照一定概率分布随机选择策略的方式称为混合策略。相应的纳什均衡被称为混合策略纳什均衡。即使在没有明确最优解的情况下,混合策略纳什均衡仍然提供了一种稳定的解决方案。当参与者选择单一确定的策略时,这种选择被称为纯策略,相应的纳什均衡则称为纯策略纳什均衡。纳什均衡包括纯策略和混合策略纳什均衡。根据纳什定理,即使在有限博弈中不存在纯策略纳什均衡,也必然存在至少一个混合策略纳什均衡。例如,在石头-剪刀-布博弈中,虽然没有纯策略纳什均衡,但存在混合策略纳什均衡。而在胆小鬼博弈中,则存在两个纯策略纳什均衡。
美国经济学家威尔逊进一步指出,纳什均衡在绝大多数情况下都是奇数个。这表明胆小鬼博弈可能还存在混合策略纳什均衡。
我们还可以通过使期望支付相等的方法来计算混合策略纳什均衡。这种方法的核心在于理解参与者为何需要采用混合策略:只有当不同策略带来的期望支付相同时,参与人才会考虑使用混合策略。如果某种策略能够带来更高的期望支付,参与人自然会选择该策略,即采用纯策略。
具体来说,当参与人的各种纯策略的期望支付不相等时,他们会倾向于选择那个期望支付最高的策略。然而,当所有策略的期望支付相等时,参与者就没有动机去偏向任何一个特定的策略,这时他们就会随机选择这些策略,从而形成混合策略纳什均衡。这种情况下,任何一方都无法通过单方面改变其策略选择来增加自己的期望收益。
在胆小鬼博弈中,假设甲和乙分别以\(p\)和\(q\)的概率选择退让。如果乙的选择使得甲选择退让和直行的期望支付无差异,则需满足:
同样地,可以计算出 \(p = 9/10\)。
因此,在胆小鬼博弈中,混合策略纳什均衡是甲和乙都以 \(9/10\) 的概率选择退让,以 \(1/10\) 的概率选择直行。
猜硬币博弈#
在猜硬币博弈中,两个参与者A和B各自持有一个硬币,并将其扣在桌子上,不让对方看到硬币的正反面。随后,两人同时把手拿开,揭示硬币的正反面。根据硬币的组合结果,双方会获得相应的支付。
通过观察支付矩阵,我们可以发现没有一个纯策略组合使得双方的选择都是对对方策略的最佳对应。因此,该博弈不存在纯策略纳什均衡。
为了找到混合策略纳什均衡,我们使用支付均等法来确定每个参与人选择不同策略的概率。假设甲和乙分别以 \(p\) 和 \(q\) 的概率选择正面,可以得到
A的最优混合策略,使B选择正面和反面的期望支付相等: $\(\begin{align*} & \quad E\pi^B(正) = E\pi^B(反) \\ \Rightarrow & \quad 3p + (-2)(1-p) = -2p + (1-p) \\ \Rightarrow & \quad p = 3/8 \end{align*} \)$
B的最优混合策略,使A选择正面和反面的期望支付相等: $\(\begin{align*} & \quad E\pi^A(正) = E\pi^A(反) \\ \Rightarrow & \quad -3q + 2(1-q) = 2q + (-1)(1-q) \\ \Rightarrow & \quad q = 3/8 \end{align*} \)$
B:正面 |
B:反面 |
|
|---|---|---|
A:正面 |
-3,3 |
2,-2 |
A:反面 |
2,-2 |
-1, 1 |
B:正面 (q) |
B:反面 (1-q) |
|
|---|---|---|
A:正面 (p) |
-3,3 |
2,-2 |
A:反面 (1-p) |
2,-2 |
-1, 1 |
因此,混合策略纳什均衡为甲和乙都以3/8的概率选择正面,以5/8的概率选择反面,简记为(\((3/8, 5/8), (3/8, 5/8)\))。
相应的,可以计算出甲和乙的平均收益分别为 \(1/8 (= 3/8*(-3) + 5/8*2)\) 和 \(-1/8 ( = 3/8*3 + 5/8*(-2))\)。这表明在混合策略纳什均衡下,甲的平均收益为正,而乙的平均收益为负。这表明甲具有优势,即使在表面上看起来公平的博弈中,从混合策略的角度来看,可能存在某种不对称性或优势。
如果我们将甲视为「庄家」(例如,一个组织者或机构),那么这个优势可能会在长期多次重复博弈中累积成显著的收益。在赌博和博彩游戏中,即使每个玩家都有一定的获胜概率,庄家通常会设置一些规则或赔率,确保自己在长期内有微小但稳定的优势。
总之,猜硬币博弈展示了即使是看似公平的博弈,从混合策略纳什均衡的角度来看,也可能存在某种不对称性或优势。这种分析有助于理解现实生活中的许多博弈和决策情境,特别是在涉及长期重复互动的情况下。
B:正面 (q) |
B:反面 (1-q) |
|
|---|---|---|
A:正面 (p) |
-3,3 |
2,-2 |
A:反面 (1-p) |
2,-2 |
-1, 1 |
A的平均收益:\(3/8*(-3) + 5/8*2 = 1/8\)
B的平均收益:\(3/8*(3) + 5/8*(-2) = -1/8\)
市民责任博弈#
市民责任博弈描述了在面对公共安全问题时,个人之间的策略选择及其相互影响。例如,甲和乙目睹了一起抢劫案,两人都希望有人报警来制止犯罪。如果抢劫未能得逞,每人将获得10单位的支付增加;然而,去报警会减少3单位的支付。支付矩阵如下所示:
check
在该博弈中,存在两个纯策略纳什均衡;同时还有一个混合策略纳什均衡,其中每个参与者以7/10的概率选择报警,以3/10的概率选择袖手旁观。
多人市民责任博弈:假设在一个有N个参与人的市民责任博弈中,所有参与者都以 \(p\) 的概率选择袖手旁观。那么,除了甲以外,其他N-1个参与者选择袖手旁观的概率为 \(p^{N−1}\)。
为了找到混合策略纳什均衡,我们需要确保甲选择袖手旁观和报警的期望收益相等:
这意味着: $\(0∗p^{N−1}+10(1−p^{N−1})=7\)$
解这个方程,我们得到:\(p=0.3^{1/(N−1)}\)。
由此可见,随着目击者人数N的增加,每个人选择袖手旁观的概率p也会上升。即目击犯罪的人越多,每个人报警的概率就越小。这体现了搭便车心理(free-rider problem):每个人都可能期望别人去报警而自己坐享其成,从而避免付出个人成本。
这种现象揭示了集体行动中的一个常见难题,即人们倾向于依赖他人来解决问题,从而导致整体行动力的减弱。这一发现对于理解公共安全问题中的行为模式以及设计有效的激励机制具有重要意义。
旁观者效应
旁观者效应(或称基诺维斯现象)是指由于个人感知到了团体的存在,个人在某件事情上的行动力和责任感就会减弱,甚至消失,最终导致群体性的不作为。这种现象在实际案例中得到了验证,例如1964年美国纽约皇后区发生的凯瑟琳·基诺维斯(Kitty Genovese)遇害案件。尽管有多位邻居听到了凯瑟琳的呼救声,但由于大家都以为他人会报警或者已经报警,最终没有及时采取行动,导致悲剧发生。
这一现象引出了如何通过制度设计和社会规范来解决这类集体行动难题的思考。有效的制度设计和社会规范可以帮助克服旁观者效应,鼓励个人在紧急情况下采取行动,从而提高社会的整体应对能力。例如,通过教育和宣传增强社会责任感,建立紧急响应机制,以及制定相关法律法规来激励个人参与公共安全事务。
拍卖博弈
拍卖博弈展示了人们在面对竞争和潜在损失时的心理动态。例如,在一美元拍卖中,出价最高者获得1美元,但出价次高者需支付自己的出价却得不到任何东西。这种机制导致了出价不断攀升,远远超出物品的实际价值,反映了人们在避免成为“次高竞价者”的心理驱动下,理性行为可能导致非理性结果。
海盗分金问题#
五个海盗抢夺了100枚金币,他们按抽签的顺序依次提出金币分配方案。具体方式如下:首先由抽到一号的海盗提出方案,所有海盗进行表决,若半数同意(包括提案者本人),则该方案通过;若未通过,则一号海盗被扔到大海里喂鲨鱼。然后由抽到二号的海盗提出方案,依次类推。
假设理性是共同知识,在保证自己生命的前提下,最大化自己的所得,并且金币的最小单位为1个金币。我们需要找到一号海盗的最优策略。
这是一个典型的动态博弈问题,因为参与人的行动有先后顺序,后行动的人能够观察到之前行动人的选择,并据此做出决策。在这样的博弈中,我们可以使用逆向归纳法(Backward Induction)来找出纳什均衡解。
逆向归纳法:从最后一个阶段开始向前推理的方法,逐步确定每个参与者在每一步的最佳策略。
基于逆向归纳法,我们可以这样分析:
假定一到三号海盗都被扔进大海:
四号海盗只需要考虑自己和五号海盗。
四号海盗可以给自己100个金币,五号海盗0个金币。四号海盗会投票支持自己的方案,无论五号海盗如何选择,都会满足半数通过条件,他的方案必然会通过。
因此,四号海盗的最佳策略是给自己100个金币,五号海盗0个金币。
给定四号和五号的选择,假定一到二号海盗都被扔进大海,三号海盗需要考虑如何拉拢五号海盗的支持。
三号海盗可以给自己99个金币,五号海盗1个金币。这样,五号海盗会比在四号海盗提案时获得更多(至少1个金币而不是0个金币),因此五号海盗会支持三号海盗的方案。
因此,三号海盗的最佳策略是给自己99个金币,四号海盗0个金币,五号海盗1个金币。
给定三号、四号和五号的选择,假定一号海盗被扔进大海:
二号海盗需要考虑如何拉拢四号海盗的支持。
二号海盗可以给自己99个金币,四号海盗1个金币。这样,四号海盗会比在三号海盗提案时获得更多(至少1个金币而不是0个金币),因此四号海盗会支持二号海盗的方案。
因此,二号海盗的最佳策略是给自己99个金币,三号海盗0个金币,四号海盗1个金币,五号海盗0个金币。
给定二号、三号、四号和五号的选择,思考一号海盗的最佳策略:
一号海盗需要考虑如何拉拢三号和五号海盗的支持。
一号海盗可以给自己98个金币,二号海盗0个金币,三号海盗1个金币,四号海盗0个金币,五号海盗1个金币。这样,三号海盗和五号海盗都会比在二号海盗提案时获得更多(至少1个金币而不是0个金币),因此他们会支持一号海盗的方案。
因此,一号海盗的最佳策略是给自己98个金币,二号海盗0个金币,三号海盗1个金币,四号海盗0个金币,五号海盗1个金币。
通过逆向归纳法,我们找到了一号海盗的最优策略。一号海盗可以通过给自己98个金币,三号海盗1个金币,五号海盗1个金币的方式,确保他的提案能够通过,从而最大化自己的收益。
性别战#
性别战博弈(Battle of the Sexes)是一种非零和博弈,描述了两个参与人之间的冲突与合作。在这个博弈中,两个参与者(通常假设为一对情侣)必须选择一起参加一个活动,但他们对活动的偏好不同。例如,男方可能更喜欢看足球比赛,而女方可能更喜欢听音乐会。他们希望在一起度过时光,但每个人都有自己的偏好。
在标准的性别战博弈中,支付矩阵如下所示:
男生:足球 (F) 男生:音乐会 (C) 女生:足球 (F) 2, 1 0, 0 女生:音乐会 (C) 0, 0 1, 2
该博弈存在两个纯策略纳什均衡(足球,足球),(音乐会,音乐会)。
如果我们引入决策的先后性,纳什均衡会如何发生变化呢? 比如女生先选择活动,然后男生再根据女生的选择做出对应。我们可以使用博弈树来表示决策过程:
博弈树(game tree):
男生有两个信息集:一个是女生选择音乐会的情况,另一个是女生选择足球的情况。因此,男生有四个可能的策略: s_1 ={音乐会如果女生音乐会,足球如果女生足球} s_2 ={音乐会如果女生音乐会,音乐会如果女生足球} s_3 ={足球如果女生音乐会,足球如果女生足球} s_4 ={足球如果女生音乐会,音乐会如果女生足球}
纳什均衡分析#
为了找到纳什均衡,我们首先将博弈树转换为策略式表示,以便更方便地识别双方参与人的最佳对应。通过划线法,可以确定三个纯策略纳什均衡:
{{音乐会},{音乐会如果女生音乐会,足球如果女生足球}};
{{音乐会},{音乐会如果女生音乐会,音乐会如果女生足球}};
{{足球}, {足球如果女生音乐会,足球如果女生足球}}。
在博弈树中,我们可以用双线标注这些纳什均衡的路径。均衡路径是从起始结到终点结所经过的决策结和最优选择构成的路径,而非均衡路径则是那些不被选择的路径。
check add figure
在 {音乐会,s_1}中,女生选择音乐会,男生选择音乐会。 在 {音乐会,s_2}中,女生选择音乐会,男生选择音乐会。 在 {足球,s_3} 中,女生选择足球,男生选择足球。
纳什均衡存在的问题#
接下来,我们需要分析这三个纳什均衡是否都是可信或合理的。不合理的选择通常被视为包括不可信的威胁或承诺。具体来说:
在{音乐会,𝑠_2}中,如果女生偏离选择了足球,男生会偏离其策略选择足球(其支付更高),而不是坚持选择音乐会。所以当女生选择足球时,男生选择音乐会便是一个不可信的选择。
在 {足球,s_3} 中,如果女生偏离选择了音乐会,男生会偏离其策略选择音乐会(其支付更高),而不是坚持选择足球。所以当女生选择音乐会时,男生选择足球便是一个不可信的威胁。
这表明这两个均衡包含了不可信的威胁或承诺。纳什均衡不能剔除非均衡路径上的不合理选择。
序贯理性的准则#
为了克服纳什均衡中的这些问题,我们引入了序贯理性的概念。序贯理性要求每个参与者在博弈的每一个决策结上重新优化自己的选择,并且考虑到将来自己也会这样做。这意味着参与人的策略不仅在均衡路径上是最优的,在非均衡路径上也必须是最优的。序贯理性有时也称为动态一致性。
使用序贯理性的准则来识别可信的纳什均衡。在上述后两个纳什均衡中,参与人的选择在非均衡路径上并不是最优的。例如,在{音乐会,𝑠_2}中,男生“选择音乐会如果女生选择足球”是不可信的;在{足球,𝑠_3}中,男生“选择足球如果女生选择音乐会”也是不可信的。因此,这两个均衡不满足序贯理性的准则,应予以剔除。
子博弈完美纳什均衡#
基于序贯理性的准则,我们可以定义一个更强的均衡概念:子博弈完美纳什均衡。它结合了纳什均衡和序贯理性的思想。
为了理解子博弈完美纳什均衡,我们首先定义什么是子博弈:
子博弈:指含有以下三个要素的博弈:
起于一个在原博弈中单结的结点;
包括这个结的后续结和枝,以及在相应的终点结处的支付。
子博弈不能破坏博弈树的信息集。
一个策略组合如果是子博弈完美纳什均衡,那么它必须满足以下条件:
它是整个博弈的纳什均衡。 它的相关行动规则在每个子博弈上都是纳什均衡。
利用博弈树考察一个纳什均衡时,只要局限于某一个子博弈上它不再是纳什均衡,所考察的纳什均衡就不是子博弈完美纳什均衡。
在动态性别战中,有三个子博弈,我们使用逆向归纳法进行分析:
男生最后行动,所以先分析男生的选择: 如果女生选择音乐会,男生的最佳对应是选择音乐会。 如果女生选择足球,男生的最佳对应是选择足球。
女生的选择: 给定男生的对应,女生会选择音乐会,因为这样她的支付为2,而选择足球的支付为1。
综上所述,唯一的子博弈完美纳什均衡是{{音乐会},{音乐会若女生选择音乐会,足球若女生选择足球}}。,即女生选择音乐会,男生选择音乐会如果女生选择音乐会,男生选择足球如果女生选择足球。 动态博弈中,决策顺序变得重要。
在动态博弈中,决策顺序变得重要。相比于纳什均衡,子博弈完美纳什均衡增加了一个约束条件,即非均衡路径上子博弈参与人策略的合理性(或威胁/承诺的可置信度)。利用逆向归纳法,我们可以剔除这些不可信的威胁或承诺,从而得到更加可信的结果。
