因果图(Causal Graph)#
import networkx as nx
# import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.iolib.summary2 import summary_col
np.random.seed(1000)
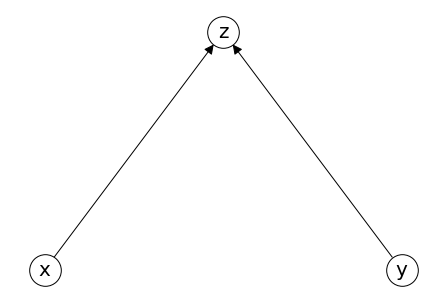
Collider (对撞结构)#
Suppose z is collider, x influence z, and y influence z, no relationship between x and y
draw_options = {
"arrowsize": 20,
"font_size": 20,
"node_size": 1000,
"node_color": "white",
"edgecolors": "black",
"linewidths": 1,
"width": 1,
"with_labels": True,
}
# 构建有向图并添加结点和边
Collider = nx.DiGraph()
Collider.add_nodes_from(list('xyz'))
Collider.add_edges_from([('x','z'),('y','z')])
pos = {'x': (-0.3,0), 'z': (0,0.2), 'y': (0.3,0)}
nx.draw(Collider, **draw_options,pos =pos)
# generate x, y
x = 10+50*np.random.randn(100000)
y = -20 + 30*np.random.rand(100000)
print(np.corrcoef(x,y)[0,1])
# generate z
z = x + y + 1.5*np.random.randn(100000)
0.00035713020604406597
fit model
(1) \(y_i = \alpha + \beta x_i +\epsilon_i\)
(2) \(y_i = \alpha + \beta x_i + \gamma z_i + \epsilon_i\)
cons = np.array([1]*100000)
fit = sm.OLS(endog = y, exog = np.array([cons,x]).T).fit()
# print(fit.summary())
fit2 = sm.OLS(endog = y, exog = np.array([cons,x,z]).T).fit()
#print(fit2.summary())
# Presenting result
result_table = summary_col(results = [fit, fit2],
float_format = '%.4f',
model_names = ['Model 1', 'Model 2'],
stars = True)
result_table.add_title('Model 1 v.s. Model 2')
print(result_table)
Model 1 v.s. Model 2
====================================
Model 1 Model 2
------------------------------------
R-squared 0.0000 0.9709
R-squared Adj. -0.0000 0.9709
const -4.9667*** -0.1411***
(0.0279) (0.0054)
x1 0.0001 -0.9700***
(0.0005) (0.0005)
x2 0.9702***
(0.0005)
====================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
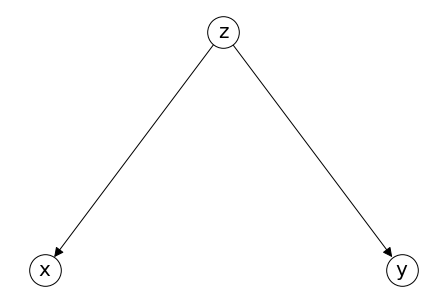
Fork#
混杂变量,confounder
# generate z,x, y
z = 200 + np.random.randn(100000)
x = 10+50*z + np.random.randn(100000)
y = -20 + 30*z + 3*np.random.rand(100000)
print(np.corrcoef(x,y)[0,1])
# # generate z
# z = x + y + 1.5*np.random.randn(100000)
cons = np.array([1]*100000)
fit = sm.OLS(endog = y, exog = np.array([cons,x]).T).fit()
# print(fit.summary())
fit2 = sm.OLS(endog = y, exog = np.array([cons,x,z]).T).fit()
#print(fit2.summary())
# Presenting result
result_table = summary_col(results = [fit, fit2],
float_format = '%.4f',
model_names = ['Model 1', 'Model 2'],
stars = True)
result_table.add_title('Model 1 v.s. Model 2')
print(result_table)
0.9993873947603757
Model 1 v.s. Model 2
======================================
Model 1 Model 2
--------------------------------------
R-squared 0.9988 0.9992
R-squared Adj. 0.9988 0.9992
const -20.1788*** -17.1419***
(0.6646) (0.5472)
x1 0.5996*** 0.0016
(0.0001) (0.0027)
x2 29.9135***
(0.1371)
======================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
draw_options = {
"arrowsize": 20,
"font_size": 20,
"node_size": 1000,
"node_color": "white",
"edgecolors": "black",
"linewidths": 1,
"width": 1,
"with_labels": True,
}
# 构建有向图并添加结点和边
Collider = nx.DiGraph()
Collider.add_nodes_from(list('xyz'))
Collider.add_edges_from([('z','x'),('z','y')])
pos = {'x': (-0.3,0), 'z': (0,0.2), 'y': (0.3,0)}
nx.draw(Collider, **draw_options,pos =pos)
draw_options = {
"arrowsize": 20,
"font_size": 20,
"node_size": 1000,
"node_color": "white",
"edgecolors": "black",
"linewidths": 1,
"width": 1,
"with_labels": True,
}
# 构建有向图并添加结点和边
G = nx.DiGraph()
G.add_nodes_from(list('ABCPQ'))
G.add_edges_from([('P','Q'),('A','P'),('A','Q')])
G.add_edges_from([('P','C'),('C','Q')])
G.add_edges_from([('B','P')])
pos = {'B': (-0.6,0), 'P': (0,0), 'Q': (0.7,0),
'A':(0.35, -0.1), 'C':(0.35,0.1)}
nx.draw(G, **draw_options,pos =pos)
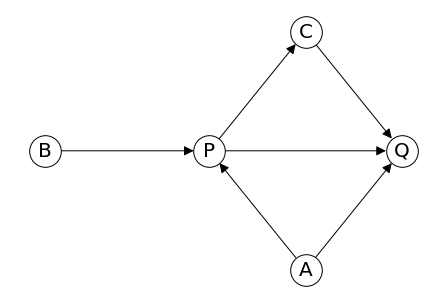
data_size = 100000
b = 100 + 10*np.random.randn(data_size)
a = 60 + 30*np.random.randn(data_size)
p = 10 + 2*b + 0.8*a + np.random.randn(data_size)
c = 2 + p + np.random.randn(data_size)
q = 400 - p + 0.2*c + 2*a + np.random.randn(data_size)
# total price effect
# q = 400.4 - 0.8*p + 2*a + noise
fit model
(1) \(q_i = \alpha + \beta p_i +\epsilon_i\)
(2) \(q_i = \alpha + \beta p_i + \gamma a_i + \epsilon_i\)
cons = np.array([1]*data_size)
fit = sm.OLS(endog = q, exog = np.array([cons,p]).T).fit()
# print(fit.summary())
fit2 = sm.OLS(endog = q, exog = np.array([cons,p, a]).T).fit()
#print(fit2.summary())
# Presenting result
result_table = summary_col(results = [fit, fit2],
float_format = '%.4f',
model_names = ['Model 1', 'Model 2'],
stars = True)
result_table.add_title('Model 1 v.s. Model 2')
print(result_table)
Model 1 v.s. Model 2
======================================
Model 1 Model 2
--------------------------------------
R-squared 0.2352 0.9995
R-squared Adj. 0.2352 0.9995
const 138.1122*** 400.4521***
(1.0109) (0.0345)
x1 0.6819*** -0.8002***
(0.0039) (0.0002)
x2 2.0001***
(0.0002)
======================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
# OLS
# ols_fit = sm.OLS(endog = q, exog = np.array([cons,p]).T).fit()
# 2SLS
iv_fit_1stage = sm.OLS(endog = p, exog = np.array([cons,b]).T).fit()
x_hat = iv_fit_1stage.predict()
iv_fit_2stage = sm.OLS(endog = q, exog = np.array([cons,x_hat]).T).fit()
# control confounder
# ols_confounder = sm.OLS(data['y'], data[['x','z']]).fit()
# presenting result
# from statsmodels.iolib.summary2 import summary_col
result_table = summary_col(results = [fit, fit2, iv_fit_2stage],
float_format = '%.4f',
model_names = ['Model1', 'Model 2', 'Model 1 with IV'],
stars = True)
result_table.add_title('IV')
print(result_table)
# print(ols_fit.summary())
# print(iv_fit_2stage.summary())
IV
======================================================
Model1 Model 2 Model 1 with IV
------------------------------------------------------
R-squared 0.2352 0.9995 0.1324
R-squared Adj. 0.2352 0.9995 0.1324
const 138.1122*** 400.4521*** 521.4658***
(1.0109) (0.0345) (1.6836)
x1 0.6819*** -0.8002*** -0.8037***
(0.0039) (0.0002) (0.0065)
x2 2.0001***
(0.0002)
======================================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
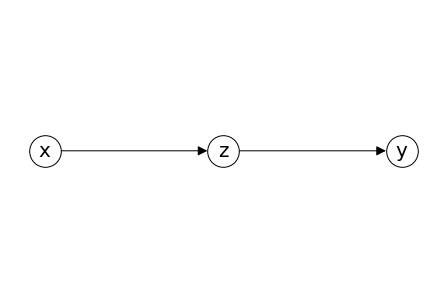
Chain#
draw_options = {
"arrowsize": 20,
"font_size": 20,
"node_size": 1000,
"node_color": "white",
"edgecolors": "black",
"linewidths": 1,
"width": 1,
"with_labels": True,
}
# 构建有向图并添加结点和边
chain = nx.DiGraph()
chain.add_nodes_from(list('xyz'))
chain.add_edges_from([('x','z'),('z','y')])
pos = {'x': (-0.3,0), 'z': (0,0), 'y': (0.3,0)}
nx.draw(chain, **draw_options,pos =pos)
data_size = 100000
x = 100 + 10*np.random.randn(data_size)
z = 3*x+ np.random.randn(data_size)
y = 5*z+ np.random.randn(data_size)
fit model
(1) \(y_i = \alpha + \beta x_i +\epsilon_i\)
(2) \(y_i = \alpha + \beta x_i + \gamma z_i + \epsilon_i\)
cons = np.array([1]*data_size)
fit = sm.OLS(endog = y, exog = np.array([cons,x]).T).fit()
# print(fit.summary())
fit2 = sm.OLS(endog = y, exog = np.array([cons,x, z]).T).fit()
#print(fit2.summary())
# Presenting result
result_table = summary_col(results = [fit, fit2],
float_format = '%.4f',
model_names = ['Model 1', 'Model 2'],
stars = True)
result_table.add_title('Model 1 v.s. Model 2')
print(result_table)
Model 1 v.s. Model 2
===================================
Model 1 Model 2
-----------------------------------
R-squared 0.9988 1.0000
R-squared Adj. 0.9988 1.0000
const -0.4012** -0.0434
(0.1620) (0.0316)
x1 15.0039*** -0.0024
(0.0016) (0.0094)
x2 5.0010***
(0.0031)
===================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
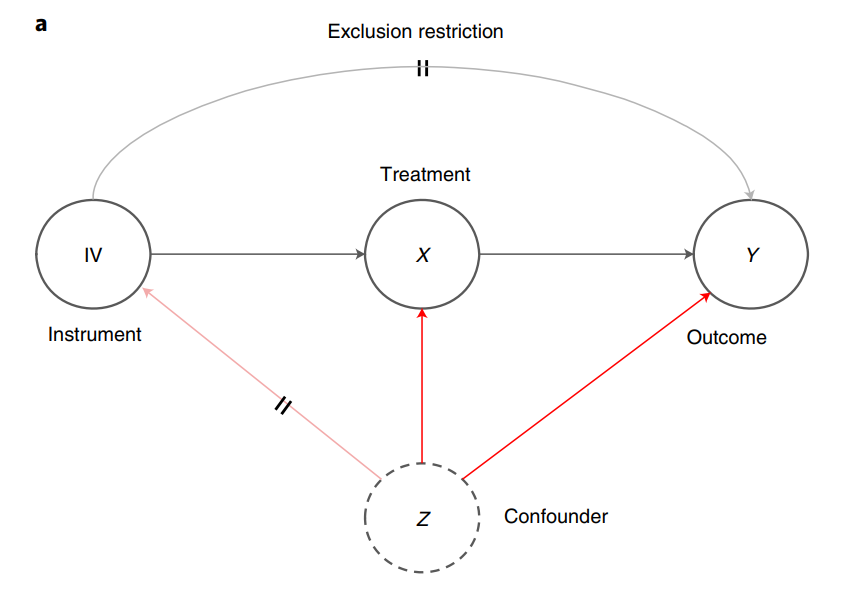
Simulation Practice: Quantifying causality in data science with quasi-experiments#
IV simu#
causal graph:
np.random.seed(2021)
z = np.random.randn()
1.1 Simu data#
import random
random.seed(2021) #设定种子
# generate IV , X , Z and Y
iv = np.array([random.gauss(10,10) for i in range(5000)])
z = np.array([random.randrange(-30,30) for i in range(5000)])
x = 3*iv + 2*z+ np.array([random.gauss(0,1) for i in range(5000)])
y = 4*x + 6*z + np.array([random.gauss(0,1) for i in range(5000)])
print('IV first 20 data: ')
print(iv[0:20])
print('-'*20)
print('y first 20 data: ')
print(y[0:20])
print('-'*20)
IV first 20 data:
[ 20.20586392 -6.93081101 2.74935374 7.9373736 -7.82976154
-10.22917018 6.41968456 10.59498401 8.58104578 21.26374151
15.07168142 6.92463389 17.90393551 -4.47388035 4.1944725
-1.18214967 27.76604789 15.89608828 3.46856887 11.36222159]
--------------------
y first 20 data:
[-186.54764132 89.24934793 -115.40383367 -17.07299347 -192.41523531
-208.01767037 -220.04205714 259.29547667 398.37124418 213.11254403
192.87980195 486.78183573 21.63838191 261.54467099 -160.23441493
50.70465479 292.82361655 485.63725094 195.58686214 34.25125174]
--------------------
import pandas as pd
df = pd.DataFrame([y,x,z,iv])
data = pd.DataFrame(df.values.T,columns = ['y','x','z','iv'])
1.2 Regression#
import statsmodels.api as sm
# OLS
ols_fit = sm.OLS(endog = y, exog=x).fit()
# 2SLS
iv_fit_1stage = sm.OLS(endog = x, exog = iv).fit()
x_hat = iv_fit_1stage.predict()
iv_fit_2stage = sm.OLS(endog = y, exog = x_hat).fit()
# control confounder
ols_confounder = sm.OLS(data['y'], data[['x','z']]).fit()
# presenting result
from statsmodels.iolib.summary2 import summary_col
result_table = summary_col(results = [ols_fit, iv_fit_2stage, ols_confounder],
float_format = '%.4f',
model_names = ['OLS', '2SLS','control confounder'],
stars = True)
result_table.add_title('OLS v.s. 2SLS')
print(result_table)
# print(ols_fit.summary())
# print(iv_fit_2stage.summary())
OLS v.s. 2SLS
=====================================================
OLS 2SLS control confounder
-----------------------------------------------------
R-squared 0.9231 0.3286 1.0000
R-squared Adj. 0.9231 0.3285 1.0000
x 4.0001***
(0.0003)
x1 5.1567*** 3.9553***
(0.0211) (0.0800)
z 6.0000***
(0.0010)
=====================================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
1.3 simulating cofficient for 200 times#
def reg_result():
# generate IV , X , Z and Y
iv = np.array([random.gauss(10,10) for i in range(5000)])
z = np.array([random.randrange(-30,30) for i in range(5000)])
x = 3*iv + 2*z+ np.array([random.gauss(0,1) for i in range(5000)])
y = 4*x + 5*z + np.array([random.gauss(0,1) for i in range(5000)])
# regression
ols_fit = sm.OLS(endog = y, exog=x).fit()
# 2SLS
iv_fit_1stage = sm.OLS(endog = x, exog = iv).fit()
x_hat = iv_fit_1stage.predict()
iv_fit_2stage = sm.OLS(endog = y, exog = x_hat).fit()
return ols_fit.params[0], iv_fit_2stage.params[0]
ols = []
tsls = []
for i in range(500):
a,b=reg_result()
ols.append(a)
tsls.append(b)
from matplotlib import pyplot as plt
true_effect = 4
x = [true_effect]*120
y = range(0,120)
plt.figure(figsize=(20,8),dpi=80)
plt.plot(x,y, '--', color='black',linewidth = 3)
plt.hist(ols)
plt.hist(tsls)
plt.show()

# 如果IV 影響y呢? relax Exclusion Restriction
def reg_result():
# generate IV , X , Z and Y
iv = np.array([random.gauss(10,10) for i in range(5000)])
z = np.array([random.randrange(-30,30) for i in range(5000)])
x = 3*iv + 2*z+ np.array([random.gauss(0,1) for i in range(5000)])
y = 4*x + 5*z + 4*iv+ np.array([random.gauss(0,1) for i in range(5000)])
# regression
ols_fit = sm.OLS(endog = y, exog=x).fit()
# 2SLS
iv_fit_1stage = sm.OLS(endog = x, exog = iv).fit()
x_hat = iv_fit_1stage.predict()
iv_fit_2stage = sm.OLS(endog = y, exog = x_hat).fit()
return ols_fit.params[0], iv_fit_2stage.params[0]
ols = []
tsls = []
for i in range(500):
a,b=reg_result()
ols.append(a)
tsls.append(b)
from matplotlib import pyplot as plt
true_effect = 4
x = [true_effect]*120
y = range(0,120)
plt.figure(figsize=(20,8),dpi=80)
plt.plot(x,y, '--', color='black',linewidth = 3)
plt.hist(ols)
plt.hist(tsls)
plt.show()

