成本函数#

商品的定价策略和生产决策与企业的成本结构息息相关。了解企业的成本结构对于理解企业的经济决策和市场竞争至关重要。本部分将学习生产成本的结构和特征，其中成本的关键影响因素是企业在每个生产周期内的产量。在此过程中，我们假设要素价格是外生的，与企业的生产决策无关。

首先，我们将学习如何从生产函数中推导出成本函数。成本函数表达的是产量与最低成本之间的关系，是成本最小化问题的值函数。企业的生产成本由生产技术和要素投入的价格共同决定。

其次，我们将探讨成本结构的划分和特征。成本可以分为可变成本和固定成本。了解成本是固定还是可变对企业管理至关重要。当企业计划增加或减少生产时，它希望知道这种变化将如何影响其成本。可变成本是随着产量变化而变化的费用，例如原材料和劳动力。固定成本则是与企业生产规模无关的费用。固定成本对企业的生产决策没有影响。我们还将介绍另一种成本结构的划分方式：可变成本和上头成本。

最后，我们将学习如何绘制长期和短期的成本曲线，并探讨它们之间的关系。我们将理解企业生产技术特点如何在短期和长期内影响成本。没有成本曲线就没有供应曲线，也就无法全面了解市场的供求关系及其变化。在短期中，除了固定成本曲线外，各种成本曲线的形状受到边际产量递减规律的制约。而在长期中，成本曲线的形状则基于现实考量，受到规模经济和不经济的限制。

学习目标

  • 理解成本结构的分类和特征：理解可变成本和固定成本的定义和区别，了解它们对企业经营决策的影响。

  • 掌握成本函数的推导方法：能够从生产函数推导成本函数。

  • 分析成本曲线及其关系：能够绘制长期和短期的成本曲线，理解不同成本曲线的形状和特点，以及它们之间的关系。

由生产函数到成本函数#

在生产部分, 我们分析了企业的是成本最小化问题。我们将该问题的值函数称为成本函数，即，

\[\begin{split} \begin{align} C(Q,w,r) &= & min_{K,L} \ wK+rL\\ && s.t. f(K,L) = Q \end{align} \end{split}\]

成本函数，\(C(Q,w,r)\)，是关于产量和要素价格的函数，表示在给定产量下的最小成本。推导成本函数的过程可分为以下两步：

  • 第一步：通过求解成本最小化问题，得到生产要素的条件要素需求函数：

\[\begin{split} \begin{align*} L^* & = L(Q,w,r)\\ K^* & = K(Q,w,r) \end{align*} \end{split}\]

  • 第二步：将要素价格与对应的条件要素需求函数相乘并加总，即可得到成本函数：

\[ C(Q,w,r) = wL(Q,w,r) + rK(Q,w,r) \]

成本函数也可以理解为扩展线上的要素组合所对应的产量与成本的关系。由于产是流量，通常隐含的时间跨度是一年，因此成本也是流量，对应于一年的支出。尽管通常不会特别提及，但我们需要记住企业的成本具有时间维度。

基于成本函数，我们将「边际成本」（Marginal Cost, MC）定义为：增加一单位产量所带来的总成本的变化，即

\[ MC = \frac{\partial C(Q,w,r)}{\partial Q} \]

考考你

练习1：柯布道格拉斯生产函数

假设生产函数为

\[ Q=L^𝒂 K^{𝟏−𝒂}，\ \ 𝒂\in(𝟎,𝟏) \]

两要素的价格分别为 \(w\) 和 \(r\)，请推导其对应的成本函数。

方法一：依据要素投入的最优条件求解。

  • 要素投入的最优条件为：\(MRTS_{LK}=\frac{w}{r}\)

首先计算\(MRTS_{LK}\)

\[ MRTS_{LK} = \frac{MP_L}{MP_k} = \frac{𝒂}{𝟏−𝒂}\frac{K}{L} \]

其次，通过最优条件，求解条件要素需求函数:

\[\begin{split} \begin{align} & \frac{𝑴𝑷_𝟏}{𝑴𝑷_𝟐} = \frac{𝒘}{r}\\ \Rightarrow \ & \frac{𝒂}{𝟏−𝒂}\frac{K}{L} = \frac{𝒘}{r} \\ \Rightarrow \ & K=\frac{𝟏−𝒂}{𝒂}\frac{w}{r} L \quad (p.1) \end{align} \end{split}\]

将（p.1）代入生产函数，\(Q = L^𝒂 K^{𝟏−𝒂}\)

\[\begin{split} \begin{align} & L^𝒂(\frac{𝟏−𝒂}{a}\frac{w}{r}L)^{𝟏−𝒂}\\ \Rightarrow \ & L^*=Q(\frac{𝟏−𝒂}{a}\frac{w}{r})^{𝒂−𝟏}\\ \Rightarrow \ & K^*=Q(\frac{𝟏−𝒂}{a}\frac{w}{r})^{𝒂} \end{align} \end{split}\]

最后，要素需求函数乘以各自价格并加总:

\[\begin{split} \begin{flalign} C(Q,w,r) & =& Q(\frac{𝟏−𝒂}{a}\frac{w}{r})^{𝒂−𝟏}*w + & Q(\frac{𝟏−𝒂}{a}\frac{w}{r})^{𝒂}*r \\ & = & a^{-a}(1-a)^{a-1}w^ar^{1-a}Q & \end{flalign} \end{split}\]

对于科布道格拉斯形式的生产函数，其成本函数是关于要素价格的科布道格拉斯形式，且边际成本为定值：

\[ MC = a^{-a}(1-a)^{a-1}w^ar^{1-a} \]

方法2：利用科布道格拉斯生产函数的性质——要素回报占比为定值——求解。

首先，基于要素回报占比为定值的性质，我们首先将要素投入用成本函数表示：

\[ L^* = \frac{aC(Q,w,r)}{w} \quad K^* = \frac{(1-a)C(Q,w,r)}{r} \]

其次，将用成本表示的要素投入代入生产函数：

\[ Q = L^𝒂 K^{𝟏−𝒂} = (\frac{aC(Q,w,r)}{w})^a(\frac{(1-a)C(Q,w,r)}{r})^{1-a} \]

求解\(C(Q,w,r)\)，可得

\[ C(Q,w,r) = a^{-a}(1-a)^{a-1}w^ar^{1-a}Q \]

练习2：里昂锡夫生产函数

假设生产函数为

\[ f(x_1,x_2)=\min{(ax_1,bx_2)} \]

要素价格分别为 \(w_1\) 和 \(w_2\)。请推导其对应的成本函数。

里昂锡夫生产函数表明在生产中，两要素需要按固定的互补比例进行生产，单独增加一种要素投入不能带来产量的增加，两要素的MRTS为0。因此，最优要素投入满足：

\[ Q = ax_1 = bx_2 \]

\(\Rightarrow\) \(x_1^* = Q/a\), \(x_2^* = Q/b\)， 成本函数为：

\[ C(Q,w_1,w_2) = w_1Q/a + w_2Q/b \]

练习3：固定替代比例生产函数

假设生产函数为

\[ f(x_1,x_2)= ax_1+bx_2 \]

要素价格分别为 \(w_1\) 和 \(w_2\)。请推导其对应的成本函数。

生产函数为固定替代比例时，\(MRTS_{12} = a/b\)，为定值，这说明我们需要分类讨论\(MRTS_{12}\)与\(w_1/w_2\)的关系，找到最优要素投入(具体分析可参见消费者理论中的最优选择部分)。

(1) 当\(a/b > w_1/w_2\): 企业只使用要素1进行生产，\(x_1^* = Q/a, \ x_2^* = 0\)

(2) 当\(a/b < w_1/w_2\): 企业只使用要素2进行生产，\(x_2^* = Q/b, \ x_1^* = 0\)

(3) 当\(a/b = w_1/w_2\): 最优要素投入组合不唯一，等产量线上的要素投入组合的成本是相等的，都是最优选择。

综上，我们可以将成本函数写为：

\[ C(Q,w_1,w_2) = min(\frac{w_1}{a},\frac{w_2}{b})Q \]

成本结构#

可变成本和固定成本#

成本可以划分为可变成本（Variable Cost, VC）和固定成本(Fixed Cost, FC)。

  • 可变成本是随产量变化而变化，不生产不需要支付的费用。可变成本依据产量计算，对应的是可变要素的调整。

  • 固定成本和产量无关，不会影响产出决策。

在长期，因为所有生产要素都是可变要素，所以没有固定定本，成本都是可变成本，长期的总成本函数可以用LTC (Long-run Total Cost) 表示。在上一部分的练习中，我们推导的都是长期成本函数。在短期，因为有固定要素，所以成本结构分为可变成本和固定成本——固定成本是企业投资进入市场之后才会出现的，短期总成本函数可以用STC (Short-run Total Cost)表示。

\[\begin{split} \begin{flalign*} STC &=& VC & + FC\\ LTC &=& VC & \end{flalign*} \end{split}\]

基于长期与短期成本结构的不同，我们可以通过成本函数的性状判断生产者是处于长期还是短期：如果成本函数中存在与产量无关的部分，如\(C = 200Q + 100\)，其中的\(100\)与产量无关，是固定成本，所以企业处于短期。

因为固定成本与产量无关，所以短期边际成本（SMC）不受固定成本（FC）的影响，对总成本和可变成本求导都可以得到边际成本。

\[ SMC = \frac{d STC}{d Q} =\frac{d (VC + FC)}{dQ}= \frac{d VC}{dQ} \]

固定成本包括什么？

我们可以将固定成本分为两部分：

一是在考虑期内已经支付且无法退回的支出,比如无法被收回的投资（通常将折旧计为固定成本），已支付的租金和利息等。

二是在考虑期内还未支付的且不可更改的与产出无关的费用，比如合约期内的固定工资、管理费用、利息、保险费用，基本的能源支出、安保、定期的维护费用等。这些费用在产量为0时仍需支付，只有当企业停止经营后才会停止支付。需要注意的是，在合约到期后，企业在签订新的合约之前，相关支出是可变成本，因为这些计划可以随预期的生产计划进行调整。

很显然，曾经支付且无法改变的支出是沉淀成本，而受合约约束或已确定的未来支出相对于生产（不停业）而言，也具有沉淀成本的含义。在经济学中，成本皆指机会成本，因此将固定成本纳入成本结构中存在逻辑问题。

在平狄克和鲁宾菲尔德的《微观经济学》一书中，作者区分了固定成本和沉淀成本（[]）。固定成本被限定为未支付的与生产无关的既定费用，不包括已支付且无法退回的支出。基于这一区分，固定成本会影响企业的停业决策——生产需要支付，退出市场则不需要支付，而沉淀成本与关门决策无关。需要注意的是，对于自购的资产，如果可以转售，也会影响停业决策，因为在停止经营时可以获得转售收入。并且，我们前面有讲到未支付的既定费用本质上是沉淀成本的含义，所以这一区分其实并没有解决将固定成本视为成本的逻辑问题。

考考你

某企业的生产函数为：

\[ Q = 10K^{2/3}+L^{1/2} \]

假设在去年年底，该企业购置了一台价值1000元的设备（\(K=1\)）。设备使用年限为5年，之后不会再有任何价值。该企业使用线性折旧的方法折旧此设备，即每年折旧费用为200元（20%*1000）。该设备除了用于生产企业的产品外没有任何其它用处，且企业仅拥有此一台设备，不会再购买更多的设备。劳动力价格\(w=2\)，请计算每年的可变成本和固定成本。

首先计算劳动力的条件要素需求函数

  • 给定\(K=1\)，\(Q = 10 + L^{1/2}\)，得到

\[\begin{split} L^d = \begin{cases} 0 & Q<10\\ (Q-10)^2 & Q\geq 10 \end{cases} \end{split}\]

可变成本为：

\[\begin{split} VC = \begin{cases} 0 & Q<10\\ 2*(Q-10)^2 & Q\geq 10 \end{cases} \end{split}\]

固定成本为设备所对应的折旧：\(FC = 200\)

可变成本和上头成本#

因为固定成本本质上具有沉淀成本的含义，那我们应该如何估计持有固定要素或合约的机会成本呢？我们接下来学习另一种成本结构的划分方式：可变成本和上头成本。

上头成本（Over-head Cost, OC）被定义为收入（R）与可变成本（VC）的差额。上头成本取决于市场，与产量无关，是企业在竞争下获得的收益。

\[ OC = R - VC \]

与固定成本一样，上头成本只有在企业进入市场并进行投资后才会存在。上头成本有以下三层含义：

  • 上头成本是收入。上头成本是企业减去可变成本后的收入。

  • 上头成本是租值。由于影响产出决策的是可变成本，只要收入不低于可变成本，生产决策就不会发生改变，因此超过可变成本部分的收入可以视为生产的租值。

  • 上头成本是成本。企业有将固定要素或合约在市场上租赁、转让或出售的选择，或者有出售业务或股权的选择，上头成本是这些选择收益（注意时间维度的调整），因此可视为是使用固定要素的成本。这时，总成本等于上头成本与可变成本之和，等于收入，这相当于从微观角度看选择。

对于上头成本，我们有三点说明。首先，在短期，企业的成本结构可能会随着时间的推移而发生变化。例如，如果时间跨度较短，很多合约无法轻易改动，如企业受员工的雇佣合同约束难以解聘员工，这将导致可变成本占比较低。随着时间跨度变长，例如两到三年，合约到期后，企业可以对合约进行调整，这些支出将转化为可变成本（签订新的合约之前），可变成本的占比将上升，企业可能会减少员工数量或者出售一些机器设备等。

其次，成本结构也会受企业合约结构的影响。比如，根据不同的合约类型，成本的调整可能会有所不同。对于件工合约和定期合约而言，前者的支付随产量发生变化，更容易进行调整，后者如果难以解除，则支付属于上头成本。如果企业将固定工资调整为底薪加上业绩提成的形式，工资既与直接成本相关，又与上头成本相关。或者企业的固定要素可以根据产量进行租用，例如厂房、专利的租赁费用会随着产量的变化而调整，那么，这些支出就是可变成本，企业没有上头成本。另一种情况是企业使用分成合约，所有要素根据收入的一定比例获得回报，这也是没有上头成本的情况。因此，合约结构的变化会导致上头成本和直接成本的分配发生变化。

再次，可变成本与上头成本之间可能存在一些模糊或灰色地带。比如当要素出现闲置时，会出现灰色地带。再如按间算工资的长期合约，灰色地带很容易出现。出现这种情况可能有两个原因：首先，时间只是一个委托之量，不是产品本身。因此，监管产量变化有较大的困难。其次，工资合约为期越长，生意的变化可能会对产量产生较大的影响（[], check pp）。

由于很多教材仍然使用固定成本和可变成本作为成本结构的划分，因此在接下来的画图分析中，我们将沿用这一划分。然而，为了保持逻辑的异质性，可以将固定成本理解为是上头成本的合理估计。但是需要记住，在沉淀成本部分，我们已经指出使用沉淀成本估计机会成本可能会导致错误的决策。

画图 —— 成本曲线#

成本函数可以由生产函数推导而来。如果我们知道生产函数，就可以绘制出成本函数。在本部分，我们并不是基于具体形式的成本函数来绘图，而是讨论短期和长期成本函数的特性及其之间的关系。

短期#

生产与成本的对偶关系#

因为成本函数由生产函数推导而来，因此生产和成本之间存在对应关系（对偶关系）。

首先，边际产量与边际成本呈反向关系。边际产量递减规律意味着边际成本最终一定是递增的。

以劳动力为唯一可变要素为例，假设单位劳动力价格为1。如表9所示，当劳动力的边际产量递增时，增加一单位产量所需劳动力的增加量递减。例如，在增加产量从1单位到2单位时，劳动力增加量为0.5单位；而在增加到3单位时，劳动力增加量为0.3单位。由于增加的劳动力递减，相应的成本增加量也递减，即边际成本递减。

相反地，如表10所示，当劳动力的边际产量递减时，增加一单位产量所需劳动力的增加量递增。例如，在从1单位增加到2单位时，劳动力增加量为0.5单位；而在增加到3单位时，劳动力增加量为1.5单位。由于增加的劳动力递增，相应的成本增加量也递增，即边际成本递增。

Table 9 劳动力的边际产量递增，边际成本递减#

TQ

L

TC

MC

1

1

1

2

1.5

1.5

0.5

3

1.8

1.8

0.3
Table 10 劳动力的边际产量递减，边际成本递增#

TQ

L

TC

MC

1

1

1

2

1.5

1.5

0.5

3

3

3

1.5

我们可以做一下简单的推导：

\[ MC = \frac{dSTC}{dQ} = \frac{dSVC}{dQ} = \frac{d L*w}{dQ} = w\frac{dL}{dQ} = w\frac{1}{MP_L} \]

显然，\(MC\)和\(MP_L\)呈反向变化。

其次，平均产量和平均可变成本也呈反向关系。简单证明如下：

\[ AVC = \frac{SVC}{Q} = \frac{L*w}{Q} = \frac{w}{AP_L} \]

短期成本线#

基于短期成本函数，我们可以画出六条相关的曲线：

  • 短期总成本线（STC）：代表企业在特定产量下所需支付的总成本，由短期可变成本（SVC）和固定成本（FC）相加得到。

  • 短期可变成本线（SVC）：表示在特定产量下，企业所需支付的可变成本。

  • 固定成本线（FC）代表在特定产量下，企业所需支付的固定成本。固定成本与产量无关。

  • 短期平均成本线（SAC）：表示在特定产量下，企业每单位产量平均需要支付的成本。SAC可以通过将STC除以产量得到。

  • 短期平均可变成本线（SAVC）：表示在特定产量下，企业每单位产量平均需要支付的可变成本。SAVC可以通过将SVC除以产量得到。

  • 短期边际成本线（SMC）：表示在特定产量下，企业增加一单位产量所需支付的额外成本。SMC可以由STC或SVC对产量求导得到。

  • 短期平均固定成本线（AFC）：代表在特定产量下，企业每单位产量平均需要支付的固定成本。AFC可以通过将FC除以产量得到。

我们首先分析短期边际成本线（SMC）的性状。由于边际产出与边际成本呈反向关系，因此边际成本线的性状受边际产出递减规律约束。如图75所示，由倒U-形的边际产出线可以推出边际成本线是U形或碗形的。

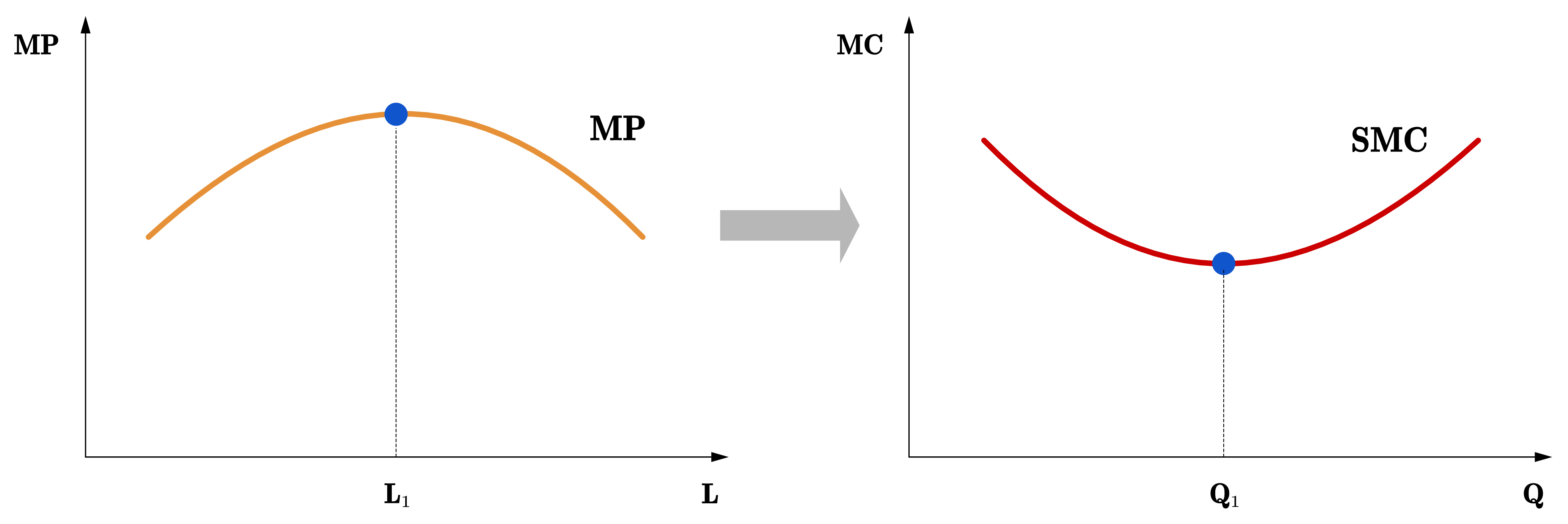
../../_images/L4-production-cost-MP-MC.png

Fig. 75 边际产量递减含义着边际成本递增，\(Q_1 = f(L_1)\)。#

其次，边际成本是可变成本（SVC）或总成本（STC）对产量的导数，即边际成本是可变成本线或总成本线切线的斜率。在边际成本的递减阶段，成本线的切线随产量的增加会越来越平坦，在边际成本的递增阶段，成本线的切线随产量的增加越来越陡峭。因此，由U形的边际成本线可以推断可变成本线和总成本线都是先凹向横轴再凸向横轴，其拐点位置为边际成本的最高点。

\[ SMC = \frac{d STC}{d Q} = \frac{d SVC}{dQ} \]

因为当\(Q=0\)时，\(SVC = 0\)， 我们可以先画出可变成本线的位置，将可变成本线垂直上移固定成本的距离，便为总成本线，如图图76所示。

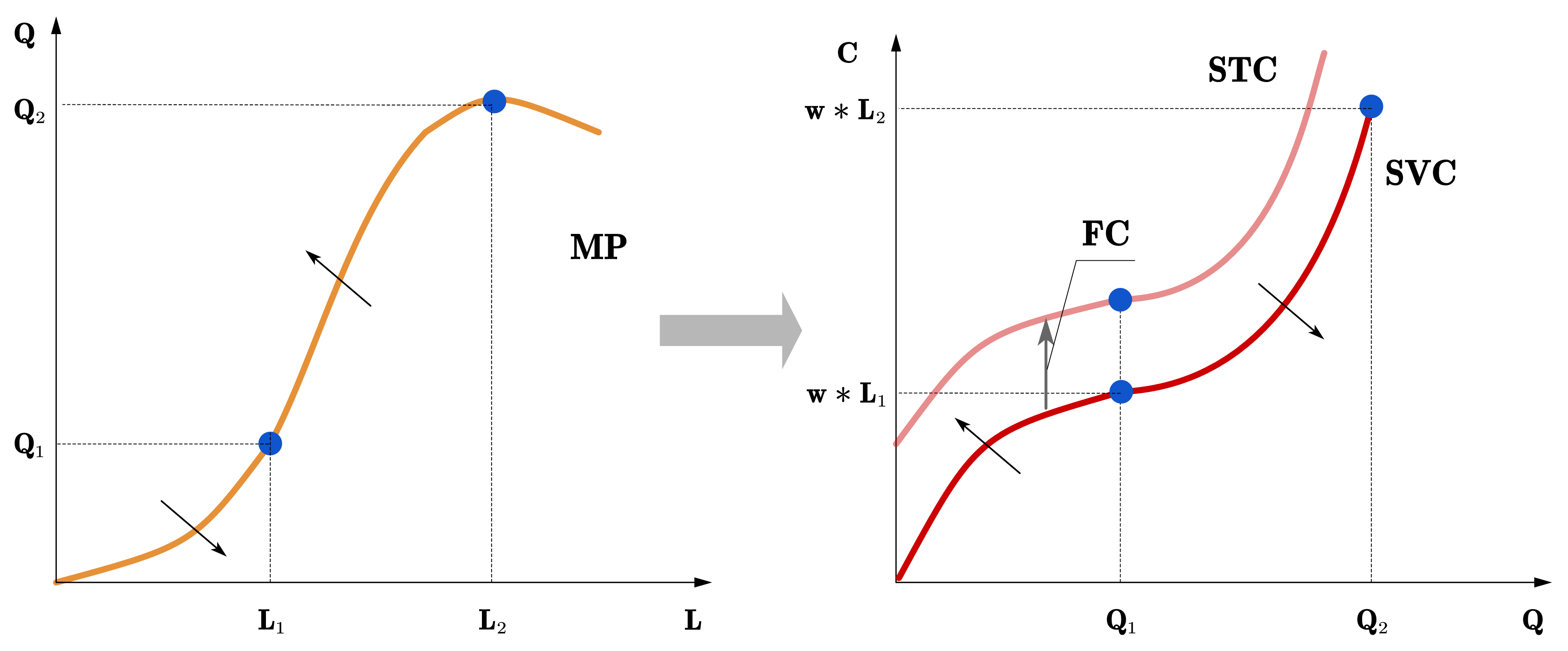
../../_images/L4-production-cost-tp-tc.png

Fig. 76 可变成本（SVC）或总成本（STC）线先凹向横轴再凸向横轴。#

再次，平均成本可以理解为是在给定产量下，成本线上的点与原点连线的斜率。由可变成本线和总成本线都是先凹向横轴再凸向横轴，可以推断短期平均成本线（SAC）和短期平均可变成本线呈U形。如图77所示， 当总成本线上的点与原点连线恰好在下方与之相切时，短期平均成本线（SAC）达到最低点。同理，当可变成本线上的点与原点连线恰好在下方与之相切时，短期平均可变成本线（SAVC）达到最低点。并且，边际成本线会通过短期平均成本线和短期平均可变成本线的最低点，即在平均（可变）成本的最低点处，边际和平均相等。因为固定成本的影响，SAVC的最低点在AVC最低点的左侧。

\[ AC = \frac{STC}{Q} = \frac{SVC + FC}{Q} = AVC + AFC \]
../../_images/L4-production-cost-avc-ac.png

Fig. 77 短期平均成本线（SAC）和短期平均可变成本线呈U形。#

证明：MC与AC相交于AC的最点。

在AC的最低点：\(\frac{dAC}{dQ}=0\)

\[ \frac{dAC}{dQ} = \frac{d(STC)/Q}{dQ}= \frac{MC*Q - STC}{Q^2} = \frac{1}{Q}(MC- AC) \]
\[ \Rightarrow \frac{dAC}{dQ}=0 \Rightarrow MC = AC \]

证明：SAVC的最低点在AVC最低点的左侧。

令 \(Q_1\)， \(Q_2\)分别为SAVC和SAC的最低点。

在SAVC的最低点： \(AC(Q_1) = MC(Q_1)\)

由\(AC = AVC+AFC\), 可以推出 \(SAC(Q_1) > MC(Q_1)\)。

所以在 \(Q_1\)处，SAC处于下降阶段，可得，\(Q_1<Q_2\)

最后，我们画出固定成本和平均固定成本线。因为固定成本为定值，所以固定成本线（FC）为水平线，总成本线和可变成本线的垂直距离为固定成本。相应的，平均固定成本线（AFC）随产量增加而递减，但不会等于0。

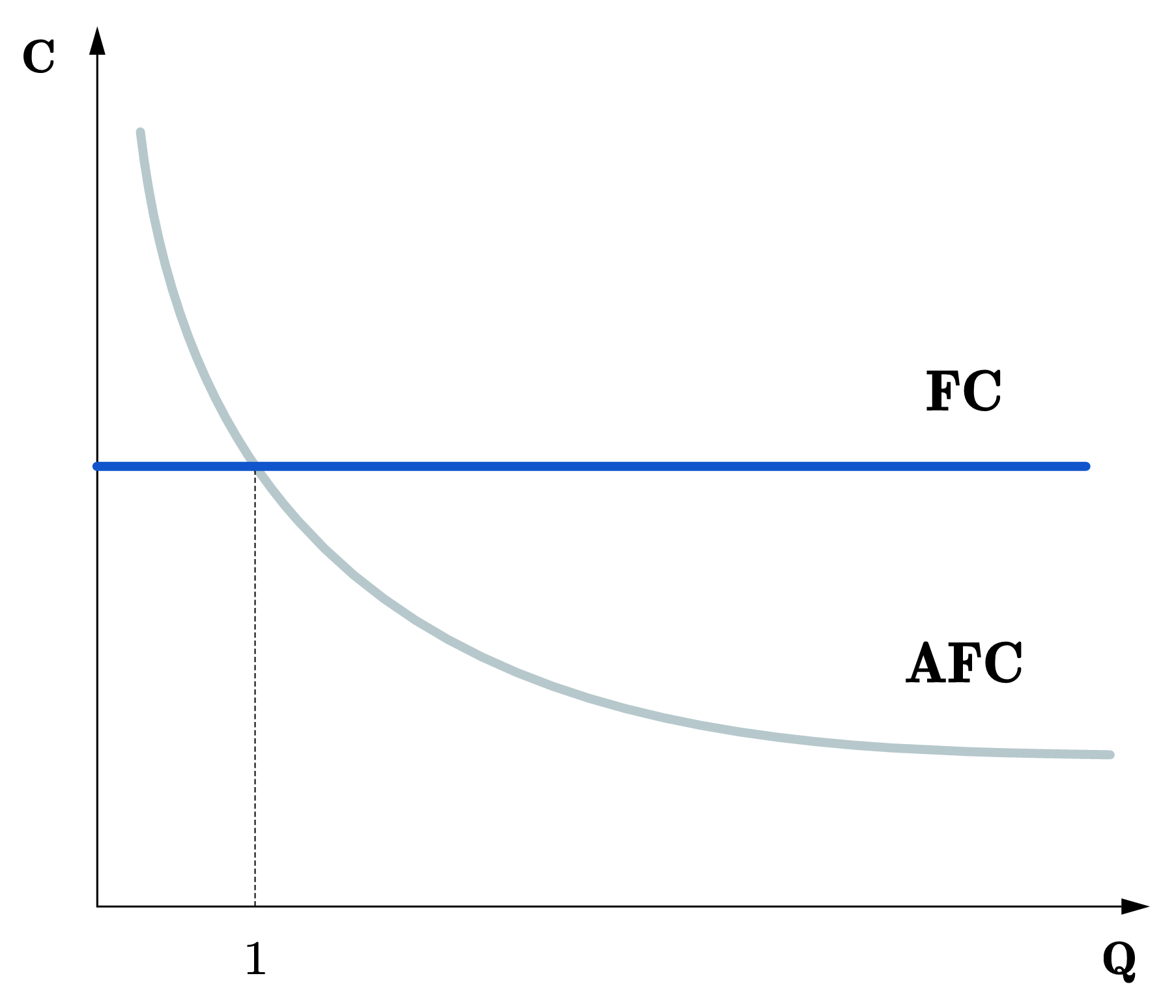
../../_images/L4-production-cost-fc.png

Fig. 78 固定成本线（FC）为水平线，平均固定成本线（AFC）随产量增加而递减。#

产能约束

在现实中，企业生产有产能约束，当产量接近约束时，MC无穷大。

../../_images/L4-production-cost-capacity-contraints.png

Fig. 79 当产量接近产能约束，\(\bar{Q}\)，时，MC无穷大。假设边际成本在每一阶段产量下为常量。#

长期#

在长期，企业的生产不再受边际产量递减规律约束。为了画长期成本曲线，有以下三点现实考虑因素。

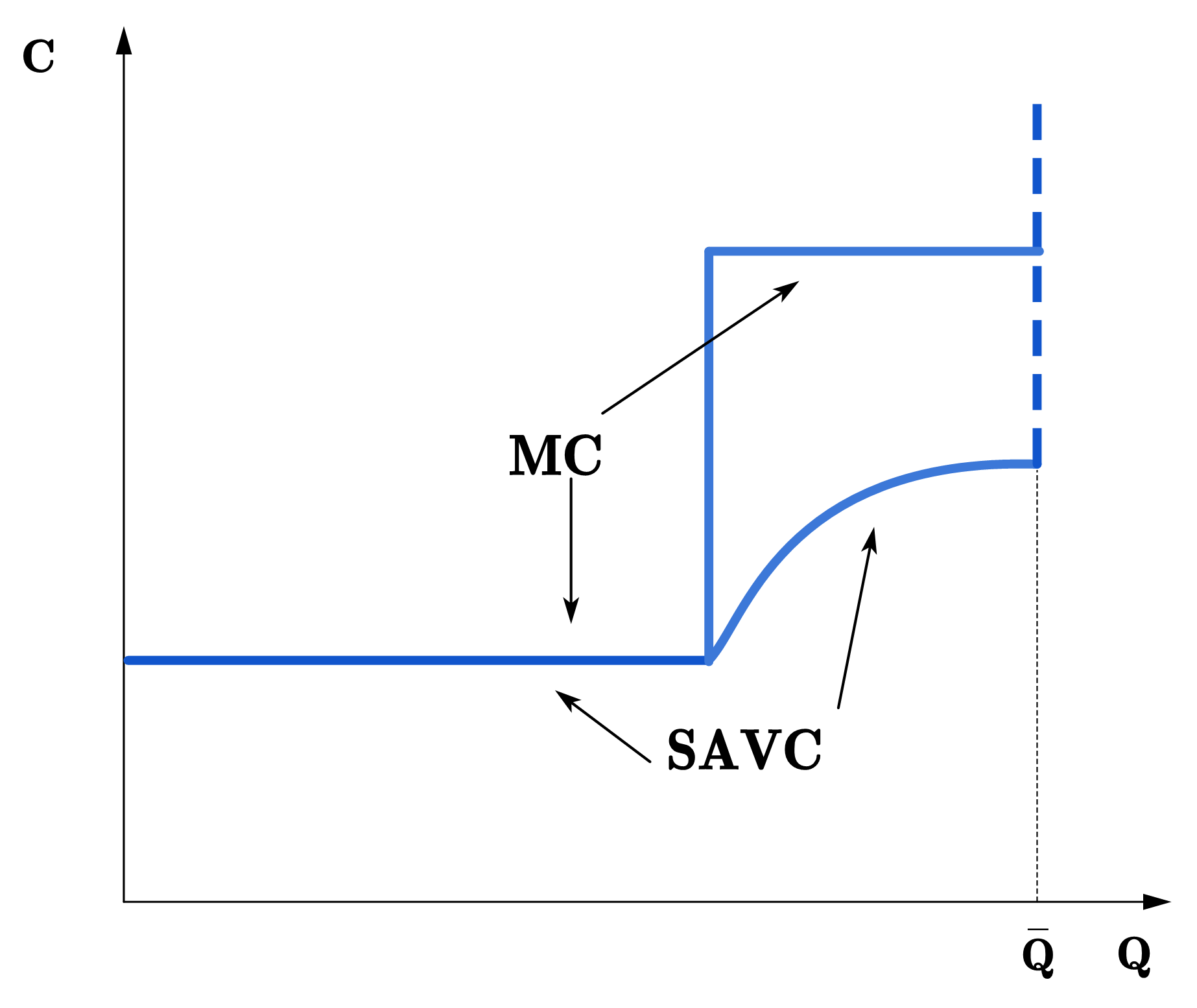
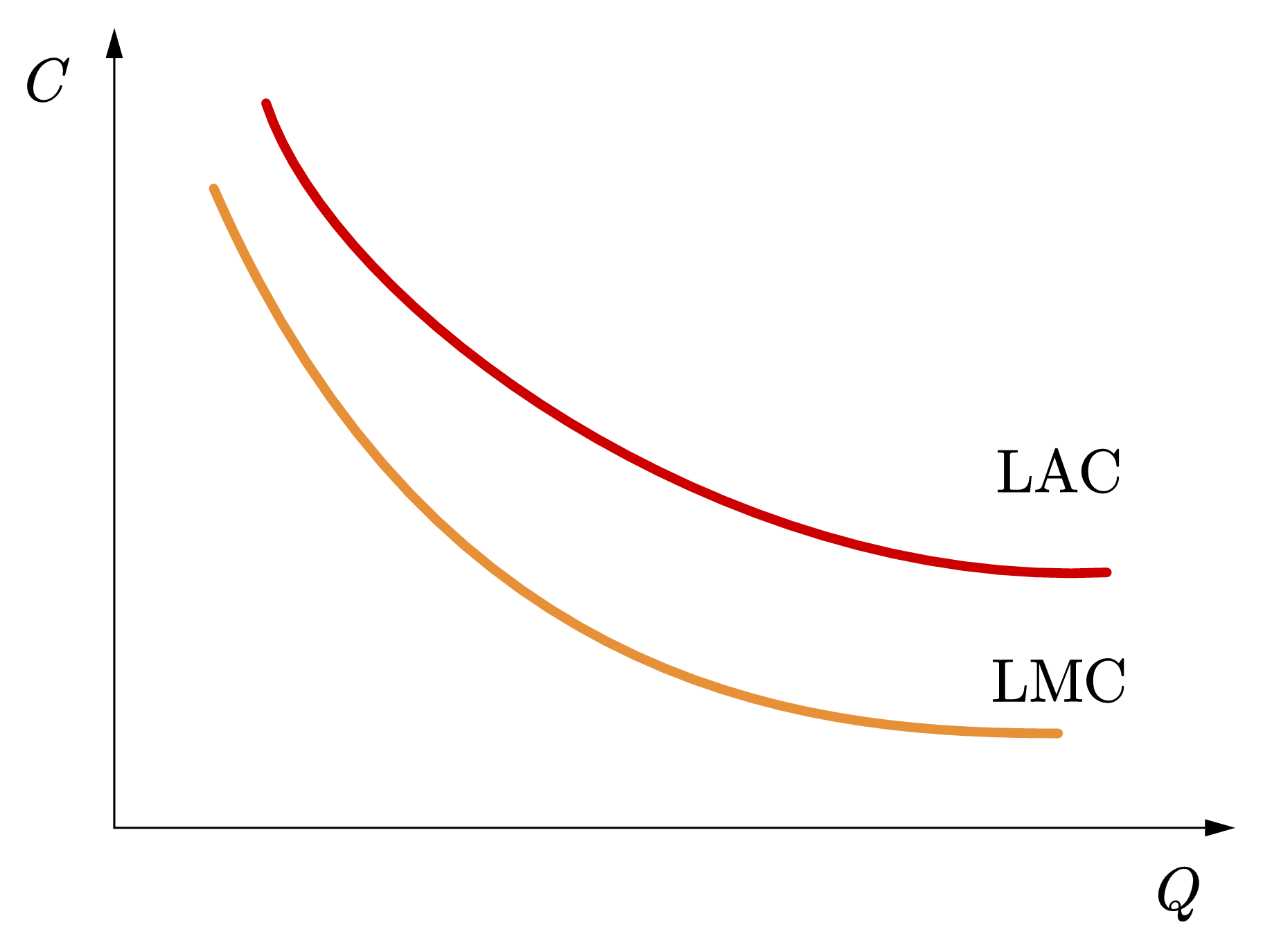
首先，我们可以看到在市场中存在竞争。这意味着企业的生产效率不会随产量的增加而持续下降，否则会导致企业一家独大。因此，如果市场存在竞争，那么平均成本曲线必然不会持续下降。图80 (a)展示了这种情况，企业的平均成本是递减的，产量越高，平均成本越低，规模越大越有优势。

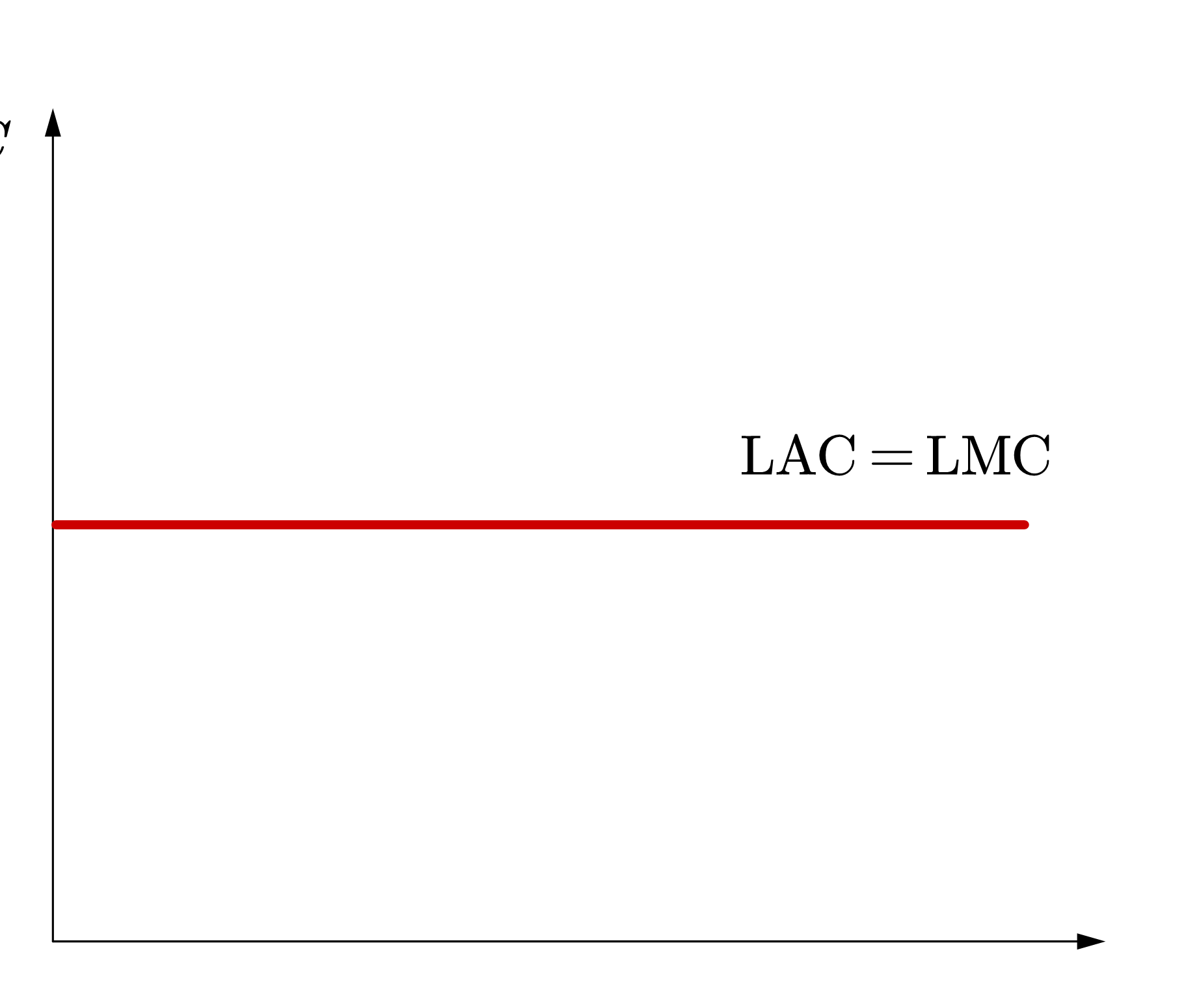
其次，市场中企业的数量是可以被决定的，不是任意或随机的。这表明市场上所有企业的生产效率不会保持恒定——平均成本等于边际成本为定值。当平均成本不受产量影响时，企业的产量是不确定的。市场上可能是有一家企业，也可能有多家企业。图80 (b)展示了这种情况。

第三，企业存在着随着产量增加而平均成本下降的阶段。

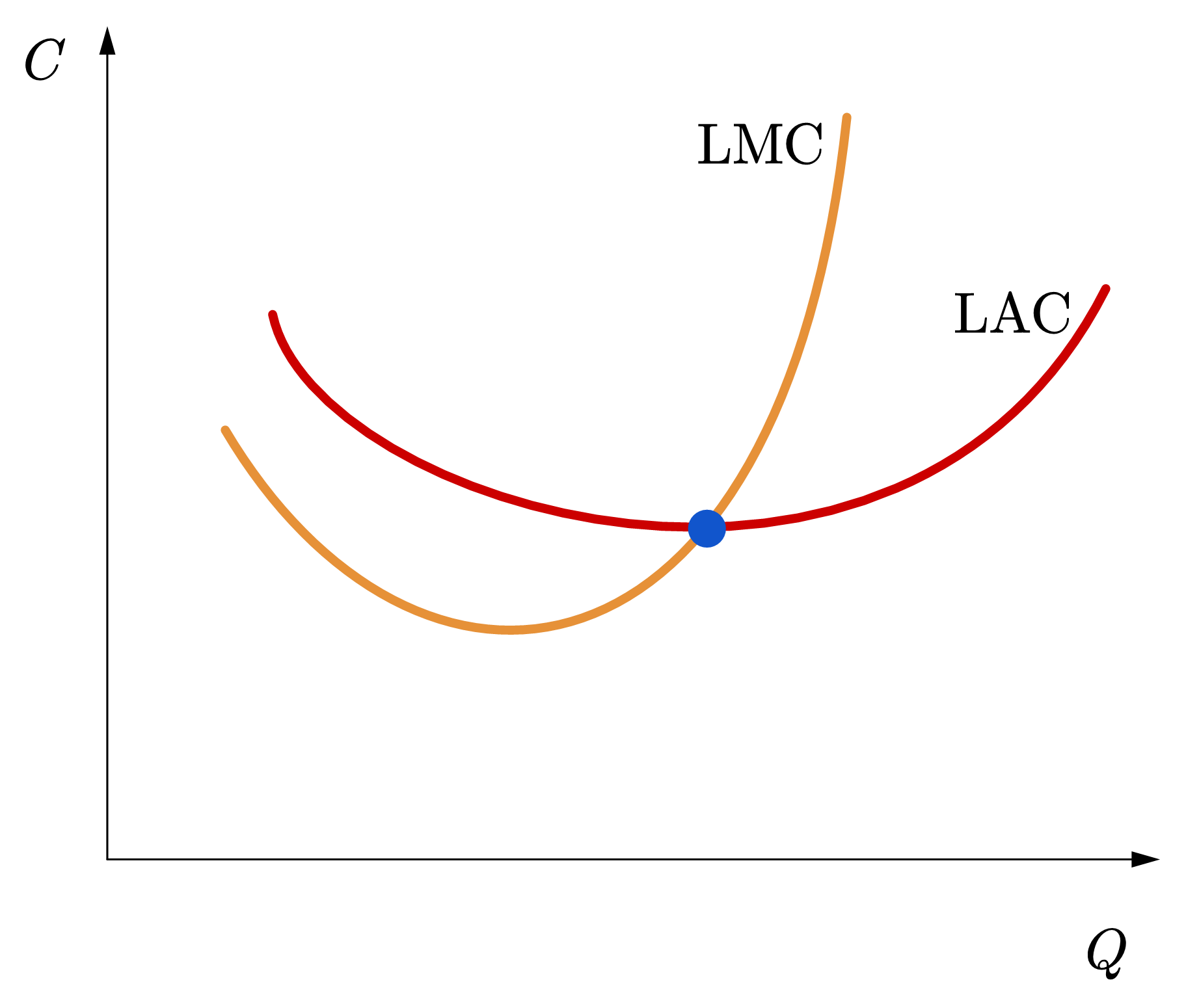
综合以上三点，我们可以得出企业的长期平均成本曲线应呈现U形或者碗形。如图80 (c)所示，U形的AC曲线表明MC曲线也是U形，通过AC曲线的最低点。因为MC等于总成本线切线的斜率，所以长期总成本线为先凹向横轴再凸向横轴。在其拐点处，对应边际成本线的最低点；平均成本线的最低点对应的是总成本线上的点与原点的连线相切于总成本线的下方。虽然长期与短期总成本线的性状是一样的，但是需要注意形成这种性状的原因是不同的。

(a) 平均成本递减 (a) 平均成本递减
(b) 平均成本为定值 (b) 平均成本为定值
(c) 平均成本为U型 (c) 平均成本为U型

Fig. 80 不同的平均成本曲线#

自然垄断

自然垄断是一个经济学中的重要概念，它与我们的日常生活息息相关。通过简单的例子，让我们一起来揭开这个神秘的面纱吧！

想象一下，你刚刚搬进了一座新城市，心满意足地准备享受新生活。但是，你突然发现只有一家供电公司在这个城市里提供电力服务。这就是一个典型的自然垄断案例。为什么会出现这种情况呢？让我们一起来探讨一下。

自然垄断的本质是由于某种特殊的经济性质，使得只有一个企业能够以更低的成本提供某种特定的商品或服务。比如电力服务的提供需要大量的设备投资和网络建设，这些成本是巨大的。如果有多家电力公司竞争，它们必须都进行重复的设备投资和网络建设，这无疑会增加整体成本，而且还会对城市的街道和地下管道造成不必要的破坏。因此，只有一家公司能够以更低的成本提供电力服务，从而形成自然垄断。

那么，自然垄断会带来什么问题呢？首先，自然垄断可能会导致市场缺乏竞争，从而使消费者失去选择权。如果只有一家电力公司，它可以随意提高价格，而消费者无法选择其他的供应商来降低成本。其次，由于市场缺乏竞争，自然垄断企业可能会滥用其市场优势地位，对消费者进行剥削。比如，它可以提供低质量的服务，而消费者无法选择其他的供应商。

针对自然垄断所带来的问题，政府可能需要采取一些措施来保护消费者的利益。一种解决办法是引入监管机构，监督自然垄断企业的行为，确保其不会滥用市场优势地位。监管机构可以设定价格上限，防止企业任意提高价格，同时也可以要求企业提供优质的服务。另一种解决办法是引入竞争机制，例如通过招标或特许经营的方式引入其他供应商，以降低成本并增加选择权。

需要注意的是，对于自然垄断的概念，学界也存在一些辩论和争议。一些学者认为自然垄断不是一个客观存在的市场现象，而是由政府干预和市场结构的失灵所导致的。自然垄断理论忽视了技术创新和市场动态变化的影响。市场竞争可以促使企业不断降低成本，提高效率，从而打破自然垄断的形成。比如通信行业，过去，传统的电话服务被认为是自然垄断的行业，因为只有一家或少数几家公司拥有固定电话网络。然而，随着移动通信技术的发展和互联网的普及，现在人们可以通过移动电话、互联网电话或即时通讯软件等多种方式进行通信，从而使得通信服务市场变得竞争激烈。

此外，张五常指出固定成本的摊薄是导致自然垄断形成的一个重要因素，使得自然垄断企业能够以更低的平均成本提供产品或服务，从而形成市场竞争障碍，使其他企业难以进入市场。 [插一下 自然垄断的定义]产量上升，平均成本不断下降。现实中不容易找到这种段的实例。183。 check

规模经济（economies of scale）和规模不经济（Diseconomies of scale）#

规模经济或规模不经济用于描述企业产量和长期平均成本的关系，属于长期范畴。规模经济是指当产量增加时，企业会获得成本优势，即平均成本随着产量的增加而递减。反之，规模不经济是指平均成本随着产量的增加而递增。我们可以说规模经济与不经济是长期平均成本曲线呈U形特征的决定因素。

规模经济可以用成本产量弹性（\(E_c\)）来衡量。

\[ E_c = \frac{dC/C}{dQ/Q} = \frac{dC}{dQ}\frac{Q}{C} = MC /AC \]

当\(E_c=1\)时，成本与产量同比例增长，既不具备规模经济也不具备规模不经济（如果投入比例是同比例变化的话，那么也具有规模报酬不变的特征）。当\(E_c >1\)时，为规模不经济，\(E_c<1\) 时，为规模经济。

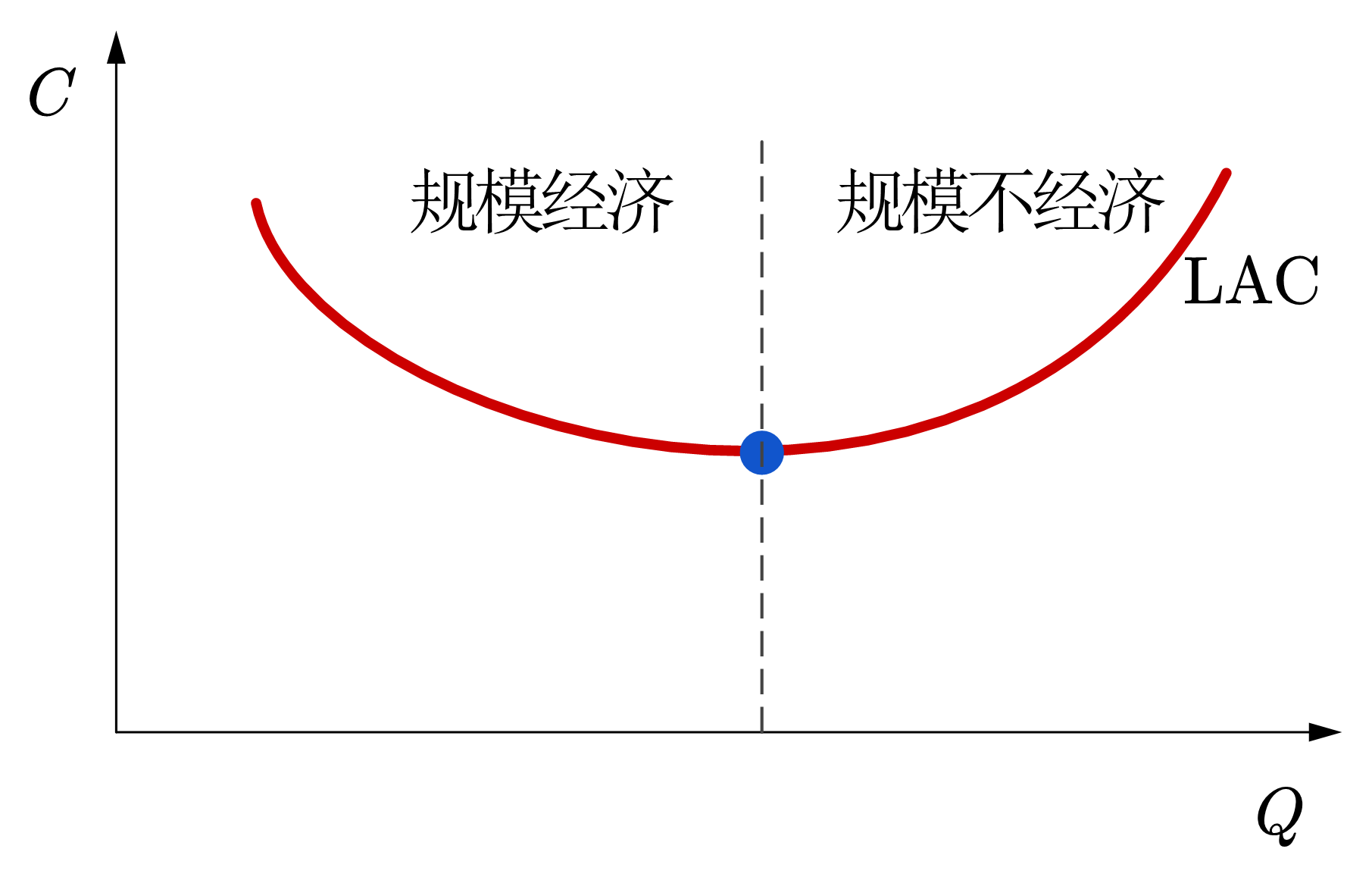
../../_images/L4-production-cost-longrun-scale-economy.png

Fig. 81 规模经济和规模不经济#

规模经济的原因：

  • 分工（Labour Division）和专业化（Specialization）。生产规模的扩大有利于分工细化，促进专业化生产，从而能够提高生产效率，降低平均成本。随着总产量增加，可供选择的成本较低的生产方法也会增多。生产方法的选择会因总产量的变化而变化。如果方法成本下降，平均成本就会下降。check 张五常book

  • 学习效应（Learning Effect）。劳动者在生产过程中能够不断积累知识和有益经验，提高工作熟练程度，从而提高生产效率和降低成本，也称为“边干边学”或“干中学”（Learning by Doing）。生产规模的扩大有利于产生学习效应。

  • 总产量越大，平均产量的交易费用越低。check p186 比如，“短暂性质的工作不容易聘得效率好的员工，就是聘得到其所需服的工资也会比较高。”

  • 生产要素价格谈判优势（Bargaining Power）：规模较大的企业对生产要素的需求更大，在购买生产要素时具有更强的谈判价格优势，可以压低要素价格，从而降低生产成本。

  • 生产有准备成本和市场成本。产量越大，可以更有效率地使用大型机器设备并更充分地利用生产要素（例如边角余料能更好地被利用），以及可以有效分担研发费用、管理成本等，有利于享受运输、采购原材料等方面的经济性。

生产准备成本和最低有效生产水平

通常情况下，生产准备成本具有不可分割性。不可分割性意味着生产准备成本无法被分割为较小的部分，需要一次性地投入，并且在特定的生产规模下才能实现经济上的可行性。这种不可分割性使得生产准备成本在企业决策中具有重要的影响。企业需要考虑到这些不可分割的成本，以确定最低有效生产水平和获利能力。

最低有效生产水平是指能够充分分摊生产准备成本，使企业能够获利进行生产的生产规模。在这一水平上，市场规模已经扩大到足够大，以使企业能够充分利用规模经济效应。在完全竞争的市场中，企业考虑进入市场时的最低有效生产水平是平均总成本的最低点。

举个例子，建造一座新的汽车生产工厂，需要大量的资本投入和复杂的设备，如装配线、机器人、涂装设备等。这些设备和资源的投资和准备是不可分割的，需要一次性的建设和布置。这涉及到土地购买、厂房建设、设备采购、供应链建立等一系列准备工作。这些准备工作需要大量的资金和时间，并且无法将其分割为较小的部分。只有当整个汽车生产工厂完全建成并投入运营后，才能开始生产汽车并实现经济上的可行性。

由于这些生产准备成本的不可分割性，汽车制造商在决策时需要充分考虑它们。建造新的汽车生产工厂需要企业进行长期规划和投资，以确保有足够的市场需求和产量以实现投资回报。如果汽车生产工厂的产能过小，无法达到经济规模，那么这些不可分割的准备成本将无法得到有效的分摊，从而降低了企业的获利能力和经济效益。

规模不经济的原因：

[]指出如果生产关系仅由技术决定，那么是不会出现规模不经济的情况。这是因为同样的技术过程可以以相同的单位成本一次又一次地使用。在现实中，生产关系还具有社会维度，是使规模不经济出现的重要潜在因素。比如，随着企业规模的增大，监控成本通常会增加，以及团队的精神或士气通常会降低。此外，随着规模的扩大，需要更多的制衡来确保生产的各个组成部分协调一致。组织越大，需要更多的制衡和文书工作。

此外，[]指出平均成本最终会上升是因为成本函数受到时间约束的影响。在给定的时间内，随着规模的增加，赶工的压力会导致成本上升（可参考张五常老师的相关著作 check）。成本曲线在横轴上的产量是与时间相关的因素（生产率）。

增加生产率的赶工可能会迫使生产者采用成本较高的方法，例如雇佣临时工或增加要素的购买。市场中的交易费用、信息费用以及合约制定的费用等都会存在。正因为这些交易费用的存在，当在赶工的情况下，做出错误的或成本较高的选择是很容易发生的。

此外，赶工会导致准备成本与市场成本之间的重复浪费。在忙乱的状态下，可能需要重复购买和准备成本，因为在赶工的情况下，常常难以做出明智和经济高效的决策。

现实中的规模经济行业

现实中，规模经济行业通常指的是那些在生产过程中固定成本非常高，只能通过扩大产量来摊薄固定成本的行业。在这里，规模经济是大规模生产带来的经济效益的简称。

在规模经济性行业中，企业面临着高额的固定成本，这些成本不随产量的增加而变化。比如，在航空工业中，航空器的研发和制造需要巨大的资金投入和设备投资，这些成本无法在短期内调整。因此，航空业企业需要通过扩大产量、提高利用率来摊薄这些高昂的固定成本。

规模经济的实现可以通过多种方式。首先，规模经济的产生与成本的分摊和效率的提高有关。随着产量的增加，企业可以分摊固定成本，从而降低单位成本。其次，规模经济还与资源的优化利用和生产效率的提高相关。通过规模扩大，企业可以更充分地利用生产设备和人力资源，提高生产效率。比如，在汽车制造业中，汽车公司面临着巨大的固定成本，例如研发和制造设施的建设费用。为了摊薄这些成本，汽车公司需要通过大规模生产来提高产量。随着产量的增加，企业可以通过资源优化和生产效率的提升来降低单位成本，从而在市场上更具竞争力。

规模经济性行业通常具有以下特征。首先，由于固定成本的高昂，规模经济性行业通常具有高度集中度，只有少数大型企业可以承担这种成本。其次，规模经济性行业具有较高的进入壁垒，其他企业很难进入市场与之竞争。这是因为在规模经济行业中，大型企业已经通过规模扩大来摊薄固定成本，从而降低了单位成本。其他企业很难在短期内达到相同的规模，因此很难与这些大型企业竞争。此外，规模经济性行业还具有较强的整合能力。通过兼并和收购等手段，大型企业可以进一步扩大规模，并通过规模经济效应降低单位成本。这使得大型企业在市场上具有更强的竞争力。

需要注意的是，虽然规模经济行业具有这些特征，但这并不意味着这些行业始终保持着高度集中度和垄断性。市场竞争、技术进步以及政府政策等因素都可能对规模经济行业的竞争环境产生影响。随着时间的推移和市场的变化，行业内的竞争格局可能发生变化，新的企业可能进入市场，竞争加剧，从而降低了行业的集中度和垄断性。此外，随着企业规模的进一步增大，可能会遇到规模不经济的情况，即单位成本的增加。这可能是由于资源的浪费、管理效率的下降以及协调的困难造成的。当企业的规模超过某个阈值时，由于规模扩大带来的管理复杂性可能会超过规模经济的优势，从而导致单位成本的增加。

外在经济（External Economics）和外在不经济（External diseconomy）#

外在经济是指外部环境的改善使得企业能够降低生产成本并提高效率的现象，即由企业所在环境和条件所带来的正面影响。在图形上，这种影响表现为长期平均成本曲线向下移动。

举例说明，假设在一个技术先进的产业集群中，企业可以与其他企业共享资源和知识，并进行合作和创新。这样一来，企业可以减少独立开展研发和生产所需的时间和成本，从而降低长期平均成本。再如，地理区位优势可能使企业能够更便捷地接触市场、供应链和交通运输，从而降低成本并提高效率。市场规模效应也可以通过大规模市场带来的需求增加来降低单位成本。此外，与供应商和合作伙伴的紧密合作可以优化供应链，提高物流和协调效率。

外在不经济是指由于外部因素的影响，使得企业出现成本增加和效率下降的现象。在图形上，外在不经济表现为长期平均成本曲线向上移动。

当企业面临资源竞争、供应链瓶颈、技术倒退或环境污染等因素的影响时，会出现外在不经济。具体而言，假设某工业区域存在多家企业，它们在生产过程中需要使用同一类资源，例如原材料或供应链服务。这些企业之间可能会发生资源的竞争，导致资源的进一步稀缺和价格的上升。这种资源争夺可能会增加企业的成本，降低效率，进而导致长期平均成本的上升。此外，如果供应链遭遇瓶颈，例如供应商的延迟交货或物流问题，企业也可能面临成本上升和效率下降的情况。技术倒退或环境污染也可能导致额外的成本和效率下降。

如图82所示，外在经济和不经济可以改变长期平均成本曲线的位置。

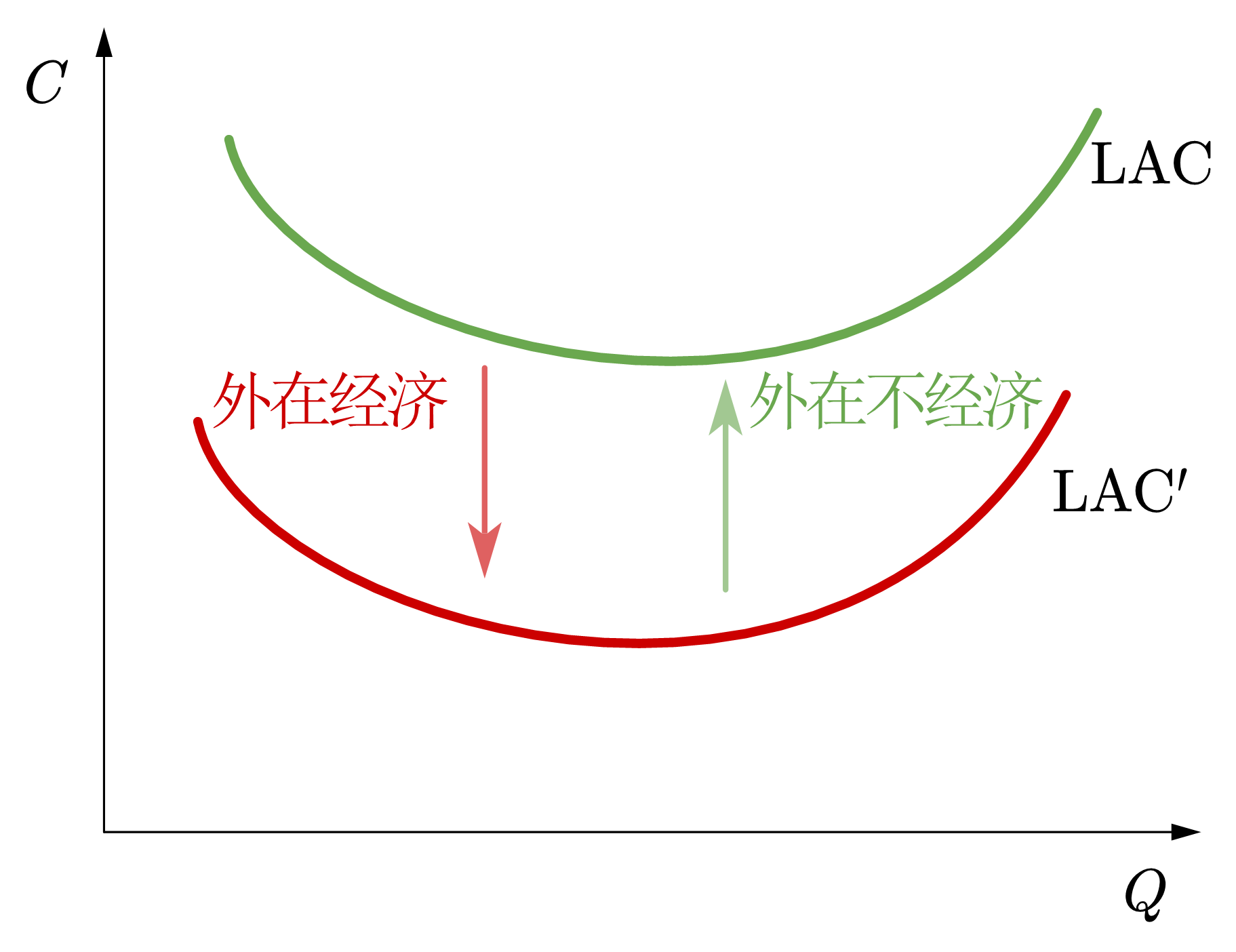
../../_images/L4-production-cost-longrun-external-economy.png

Fig. 82 外在经济和外在不经济#

范围经济（Economies of scope）和范围不经济（Diseconomies of scope）

范围经济指的是企业在同一组织内生产多种产品或提供多种服务时，可以减少成本并提高效率的现象。简而言之，范围经济是通过产品或服务的多样性来实现成本节约和效益提升。这种经济效应可以通过资源共享、技术转移、市场横向扩展等方式实现。

举个例子，假设一家食品公司既生产牛奶，又生产酸奶。由于这两种产品具有相似的生产工艺和原材料，该公司可以通过共享设备、供应链和市场渠道等资源，同时生产牛奶和酸奶。这样一来，企业可以获得规模扩大的优势，减少成本并提高效率。例如，通过在同一时间和地点生产这两种产品，可以减少生产线的闲置时间和设备的重复投资。

范围不经济则是相反的情况，指的是企业在生产多种产品或提供多种服务时，遭遇到成本上升或效率下降的现象。这种情况可能是由于资源分散、管理复杂度增加、协调困难等因素所致。范围不经济的存在可能导致成本的上升，降低企业的效率和竞争力。

比如，假设一家电子公司同时生产手机和电视。由于这两种产品需要不同的制造工艺、供应链和市场策略，公司可能需要分散资源并面临管理上的挑战。这可能导致生产效率下降、成本增加。

长期成本曲线与短期成本曲线的关系#

在短期内，企业面临固定要素，这些要素无法根据产量的变化而调整。而在长期内，所有要素都可以根据产量的变化进行调整。因此，对于给定的产量，长期总成本必然不会高于短期总成本。

如图83所示，在给定产量为\(Q_1\)的情况下，长期的最优要素投入组合是等成本线与等产量线的切点A。假设在短期内，资本是固定要素，投入量为\(\bar{K}\neq K^*\)。如果企图在短期内达到产量\(Q_1\)，劳动力投入量为\(L_1\)，很明显，这样的要素投入并不是长期的最优要素投入，会导致更高的总成本。不过，如果短期固定要素投入恰好等于\(K^*\)，那么此时短期总成本等于长期总成本。一言以蔽之，在长期，企业可以通过调整所有要素投入来实现成本的最小化。而在短期，固定要素的限制可能使企业无法达到最优要素配置，导致产生更高的总成本。

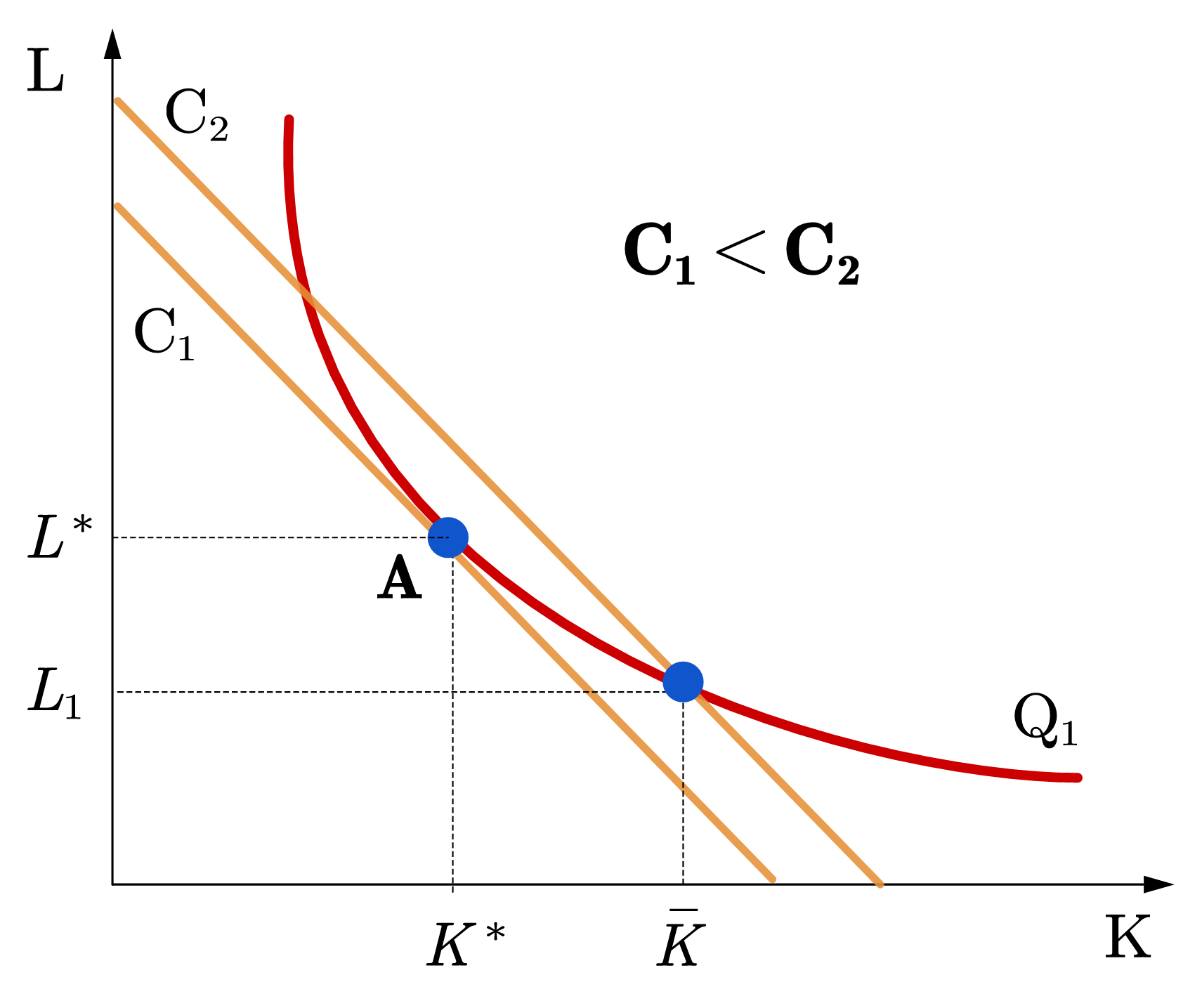
../../_images/L4-production-cost-lr-sr.png

Fig. 83 长期总成本不会高于短期总成本。#

我们也可以用式(p.1)表示长期和短期总成本的关系。如果在给定产量下，短期的固定要素（资本）投入恰好等于长期的最优资本投入，那么长期和短期总成本是相等的，否则，短期总成本必然大于长期总成本。

\[\begin{split} \begin{align} LTC(Q) \leq STC(Q |\bar{K}) & \forall Q & (p.1)\\ LTC(Q) = STC(Q | \bar{K}) & \bar{K} = K^{*}(Q) & \end{align} \end{split}\]

以上分析表明，在长期总成本线上，给定某一产量，如\(Q_1\), 我们可以找到一条短期总成本线在\(Q_1\)处与之相切，这条短期总成本线需要满足的条件是其固定要素投入（\(\bar{K}\)）等于在\(Q_1\)处的长期最优资本投入。当短期产量不等于\(Q_1\)时，由于固定要素不可调整，短期总成本必然高于长期总成本。进一步地，在图84 (a)所示的长期总成本线上，对于连续变化的每一个产量水平上，都存在一条短期总成本曲线与之相切。换句话说，长期总成本线可以有无数条短期成本曲线与之相切。这表明长期总成本线是无数条短期总成本线的包络线。类似地，在图84 (b)所示的长期平均成本曲线上，也存在无数条短期平均成本曲线与之相切，长期平均成本线是短期平均成本线的包络线。

最后，我们画出长期和短期边际成本线，如图84 (b)所示，除了边际成本线需要通过平均成本线的最低点外，由于边际成本是总成本的导数，在长期总成本和短期总成本的切点处，或者长期平均成本和短期平均成本的切点处，长期和短期边际成本是相等的。这一特征表明，当企业处于规模经济阶段（LAC下降）时：长期平均成本线（LAC）与短期平均成本线（SAC）最低点的左侧相切；长期平均成本线（LAC）与短期平均成本线（SAC）最低点的右侧相切。只有在长期平均成本线的最低点（LAC最低点），长期平均成本线（LAC）才与短期平均成本线（SAC）最低点相切。

(a) 长期和短期总成本 (a) 长期和短期总成本
(b) 长期和短期平均成本 (b) 长期和短期平均成本

Fig. 84 长期总成本线是短期总成本线的包络线，长期平均成本线是短期平均成本线的包络线。#