消费者选择：效用最大化问题 （UMP）#

消费者的选择问题可以表述为：消费者会从其可以支付的选择中（预算约束）选取其最偏好的消费束。又因为我们可以用效用函数表示偏好，所以消费者选择问题可以转化为一个数学上的最优化问题，即效用最大化问题（Utility Maximization Problem, UMP）：

\[\begin{split} \max_{x_1,x_2} u(x_1,x_2)\\ s.t. p_1x_1+p_2x_2 \leq I \end{split}\]

其中，\(p_1, p_2\)和\(I\)分别为两商品的价格和消费者的收入，是模型的外生变量。

由于偏好具有严格单调性，消费者的最优选择必然落在预算线上。若选择在预算线左侧，在预算约束下，消费者可以通过增加商品数量来提高效用。因此，上述不等式约束的最大化问题可以转化为等式约束的最大化问题：

\[\begin{split} \max_{x_1,x_2} u(x_1,x_2)\\ s.t. p_1x_1+p_2x_2 = I \end{split}\]

使效用最大化的消费束称为消费者的最优选择，或最优消费束。

最优选择的求解#

在本部分，我们选择使用几何方法来求解最优化问题。当然，我们也可以直接使用最优化方法求解，如构建拉格朗日函数或将约束条件代入目标函数，具体参见附录。几何图的优势在于可以更形象地分析和理解消费者选择问题和最优选择所需要满足的条件。

在几何图上，我们可以将最大化效用的问题转化为「固定预算线，移动无差异曲线」的问题。因为每个消费束都会有一条无差异曲线通过，所以「在预算线上寻找效用最高的消费束」的问题又可以转化为「寻找哪个消费束所对应的无差异曲线离原点最远」的问题。

那么，哪条无差异曲线会离原点最远呢？如图51所示，AB为固定的预算线，由于无差异曲线严格凸向原点，所以和预算线相切，或者说，使预算线成为切线的无差异曲线（\(I_1\)）离原点最远。在切点（\(x^1\)）处，消费者获得了最大效用——预算线上的其它消费束效用更低；效用更高的消费束消费者负担不起。切点E即为消费束就是最优选择。

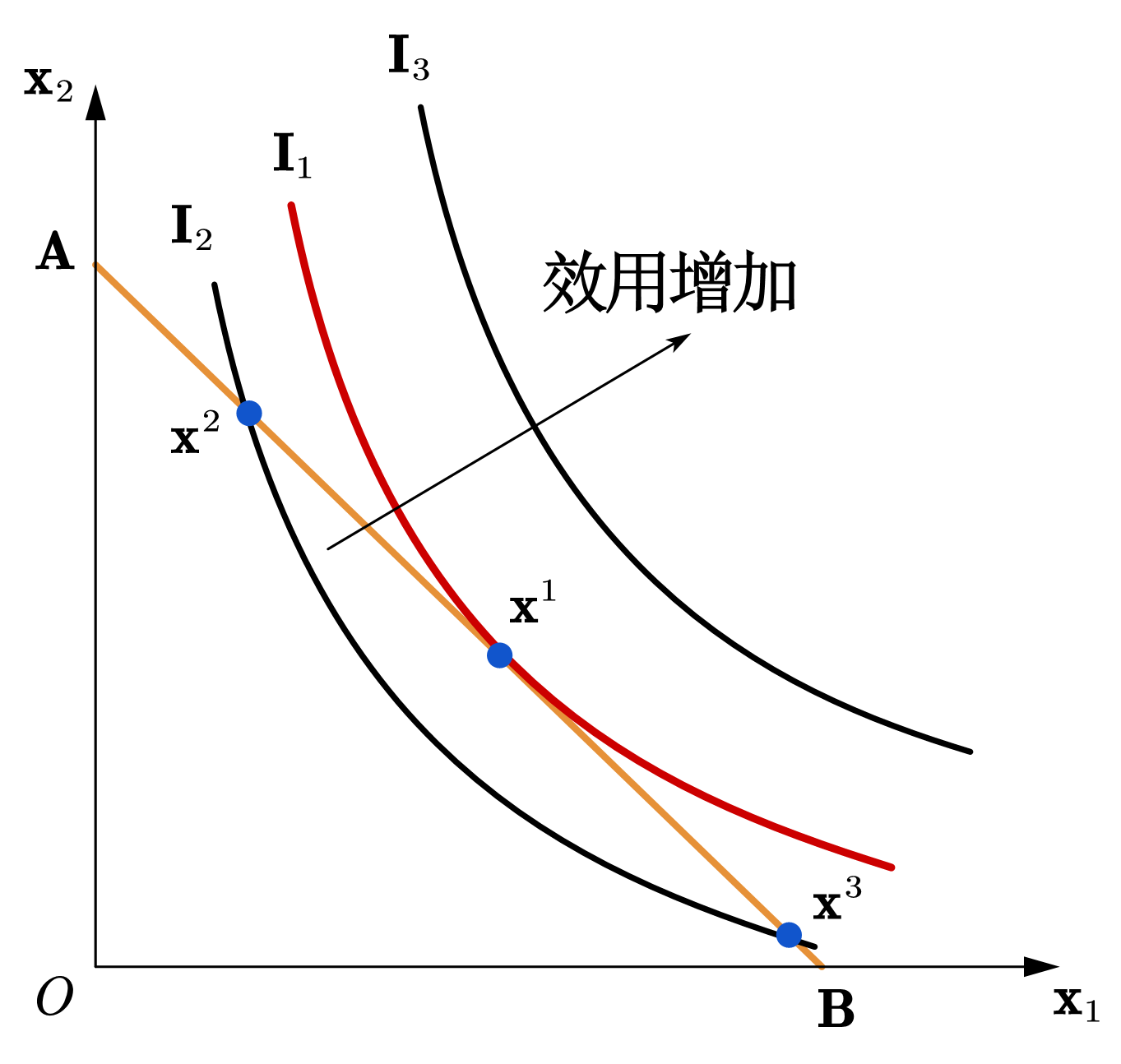
../../_images/ct-2-optimal1.png

Fig. 51 当无差异曲线与预算线相切时，消费者获得了最大效用。#

上述分析表明，消费者的最优选择应满足：

  • 预算线斜率的绝对值与商品1对商品2的边际替代率相等：\(MRS_{12} = \frac{p_1}{p_2}\)，这是消费者选择的核心条件。

  • 最优选择在预算线上：\(p_1x_1+p_2x_2 = I\)

消费者对商品的最优消费选择可以表示为价格和收入的函数，称为马歇尔需求函数：

\[x_1^* = x_1(p_1,p_2,I) \quad x_2^* = x_2(p_1,p_2,I)\]

商品的最优选择与自身价格的关系（给定另一种商品的价格和收入不变），如\(x_1(p_1,\bar{p}_2,\bar{I})\)与\(p_1\)，即为需求关系。我们在下一章会分析是否可以由最优选择推出负向的需求关系。

练习

假设某消费者的效用函数为\(U=x_1^2x_2^3\), 商品1和2的单价都为1元，收入为40元。求解消费者的最优选择。

该问题给定了商品的价格和收入，所以我们可以求解最优消费束的具体数值。

首先列出选择的最优条件：

\[\begin{split}MRS_{12} = \frac{p_1}{p_2}\\ p_1x_1+p_2x_2=I\end{split}\]

\(MRS_{12}\)可以由效用函数求计算得到：

\[MRS_{12}=\frac{MU_1}{MU_2} = \frac{2x_1x_2^3}{3x_1^2x_2^2}=\frac{2x_2}{3x_1}\]

其中，\(MU_1=\frac{\partial U}{\partial x_1}=2x_1x_2^3\)，\(MU_2=\frac{\partial U}{\partial x_2}=3x_1^2x_2^2\)。

将商品的价格和收入代入最优条件，得到

\[\begin{split}\begin{array}{lll} MRS_{12}=\frac{p_1}{p_2} &\Rightarrow &\frac{2x_2}{3x_1}=1\\ p_1x_1+p_2x_2=I&\Rightarrow& x_1+x_2=40 \end{array}\end{split}\]

两个方程两个未知数可以求解最优选择:

\[\begin{split}x_1^*=16\\ x_2^* = 24\end{split}\]

形如\(U=ax_1^\alpha x_2^\beta\)的函数（\(a,\alpha,\beta\)为参数）被称为科布-道格拉斯（Cobb-Douglas）效用函数。该效用函数的特征为最优选择的支出占比恒定，比例由商品数量的指数所决定：

\[\begin{split} \begin{align} \frac{p_1x_1^*}{I} & = &\frac{\alpha}{\alpha+\beta} \\ \frac{p_2x_2^* }{I} & = &\frac{\beta}{\alpha+\beta} \end{align} \end{split}\]

利用这个性质，我们可以快速计算消费者的最优选择，以上例为例，商品1和2的支出占比分别为\(2/5\)和\(3/5\)，则最优选择为：

\[\begin{split} \begin{align} x_1^*=\frac{2/5*I}{p_1} = \frac{2}{5}*40 = 16\\ x_2^*= \frac{3/5*I}{p_2} = \frac{3}{5}*40 = 24 \end{align} \end{split}\]

证明见附录。

当商品的价格和收入同比例变化时，消费者的最优选择是否会发生变化？

不会，因为消费者的预算线的位置不变，所以最优选择不变。

理解\(MRS_{12} = \frac{p_1}{p_2}\)的经济含义#

为什么满足\(MRS_{12} = \frac{p_1}{p_2}\)条件的消费束可以最大化效用呢？这是因为如果条件不满足时（选择仍需在预算线上），消费者可以通过调整两商品的数量以增加效用。

首先，我们思考具有\(MRS_{12} > p_1/p_2\)特征的消费束。不失一般性地，可以令\(MRS_{12} = 5\)，\(p_1/p_2=1\)，前者表示若效用不变，消费者增加一单位商品1愿意放弃五单位的商品2，后者表示在市场上，增加一单位商品1需要花费一单位商品2。

消费者会如何调整消费束呢？商品1的相对价格，\(p_1/p_2\)，表明消费者在市场上可以用一单位商品2换取一单位商品1；心理所值，\(MRS_{12}\)，表明，在如此交易后，除了可以保持效用不变外，还会多出四单位的商品2，这是因为消费者本愿意放弃五单位商品2，但是通过市场交换可以少放弃四单位，增加的四单位商品2可以带来效用的提高，所以，消费者会持续的在市场上使用商品2交换商品1，而随着商品1数量的增加，\(MRS_{12}\) 下降，交易会持续到\(MRS_{12}=p_1/p_2\)为止。

简言之，当某种商品在市场上的相对价格小于消费者的心理所值时（经济替代率小于边际替代率），消费者会通过市场交换，增加该商品在消费束中的数量。

其次，思考具有\(MRS_{12} < p_1/p_2\)特征的消费束。这个条件等价于\(MRS_{21} > p_2/p_1\)，根据上述分析，消费者会选择增加商品2和减少商品1的数量以增加效用。为了加强记忆，我们再把逻辑梳理一遍。

不失一般性地，令\(MRS_{12} = 1\)，\(p_1/p_2=5\)，表明增加一单位商品1，消费者在市场上需要支付五单位商品2，而若保持效用不变，他只愿意放弃一单位商品2，所以如果消费者增加商品1，他的效用必然会降低。而减少商品1的数量呢？ 在市场上，支付一单位商品1可获得五单位商品2，而消费者只需获得一单位商品2就可以保持效用不变，所以多出来的四单位商品2会使效用增加。因此，消费者会持续的用商品1换取商品2，直至\(MRS_{12}\)提高到等于\(p_1/p_2\)止。

因此，当某种商品在市场上的相对价格大于消费者的心理所值时（经济替代率大于边际替代率），消费者会通过市场交换，减少该商品在消费束中的数量。

我们还可以从边际效用的角度理解最优条件，将\(MRS_{12} = \frac{p_1}{p_2}\)调整为：

\[ MRS_{12} = \frac{MU_1}{MU_2} = \frac{p_1}{p_2}\Rightarrow \frac{MU_1}{p_1} = \frac{MU_2}{p_2} \]

边际效用与价格之比可以称为用价格标准化的边际效用，代表对商品支付的最后一块钱所能带来的边际效用。比如，\(MU_1/p_1 > MU_2/p_2\)（\(MRS_{12} > p1/p2\)）表明将最后一块钱花在商品1上的边际效用高于商品2，若将商品1的支出增加一块钱，商品2的支出减少一块钱，效用的变化为\(MU_1/p_1- MU_2/p_2 >0\)，所以，增加商品1会带来效用的增加；反之，减少商品1会带来效用的增加；当两种商品增加最后一块钱所带来的效用相等时，效用达到最大值。

我们可以很容易地将此条件扩展到n种商品上：当消费者面对n种商品的选择时，最大化效用的条件是每种商品所支付的最后一块钱所带来的边际效用相等，

\[ \frac{MU_1}{p_1} = \frac{MU_2}{p_2}=\cdots = \frac{MU_n}{p_n} \]

需要注意的是，我们关注的问题是消费者会如何进行选择，上面所举的不满足最优条件的情况可以视为消费者在选择前所做的假想情景分析，相应的，在市场上所做的商品数量调整也是头脑中的分析，而不是真实进行的。

练习#

练习1#

小明喜欢包子和油条，他的等优曲线凸向原点，且不与坐标轴相交。油条价格为1元，包子为3元。小明将收入都花费在这两者上，并且他所预想选择的物品组合意味着油条对包子的边际替代率为2。请问：小明的消费组合是否是最优的？ 如果不是，他应该如何调整呢？

在此问题中，油条的相对价格为1/3个包子，即增加1单位油条，需要放弃1/3个包子，而油条对包子的边际替代率为2，两者不相等，显然不是最优选择。那小明应该如何调整油条和包子的数量呢？

增加一根油条，小明愿意放弃2个包子，而在市场上只需要放弃1/3个包子，所以用1/3个包子换得油条后，不但可以维持效用不变，还可以多出5/3个包子，多出的包子会带来效用的增加。所以小明会增加油条，减少包子的数量。

或者，油条对包子的MRS大于两者价格之比可得：

\[ MU_油条/p_油条 > MU_包子/p_包子 \]

说明在油条上所花费的最后一块钱的边际效用大于在包子上所花费的最后一块钱的边际效用，所以增加油条的支出会带来效用的增加。

练习2#

对于完全互补品和完全替代品，消费者应如何决定最优选择呢？

对于完全互补品，两种商品必须依据一定比例共同消费，单独增加一种商品的数量不会影响效用。所以，最优选择的消费束也应满足既定的比例，如图52所示，在预算线AB上，无差异曲线\(I_1\)的拐点处恰为最优选择。

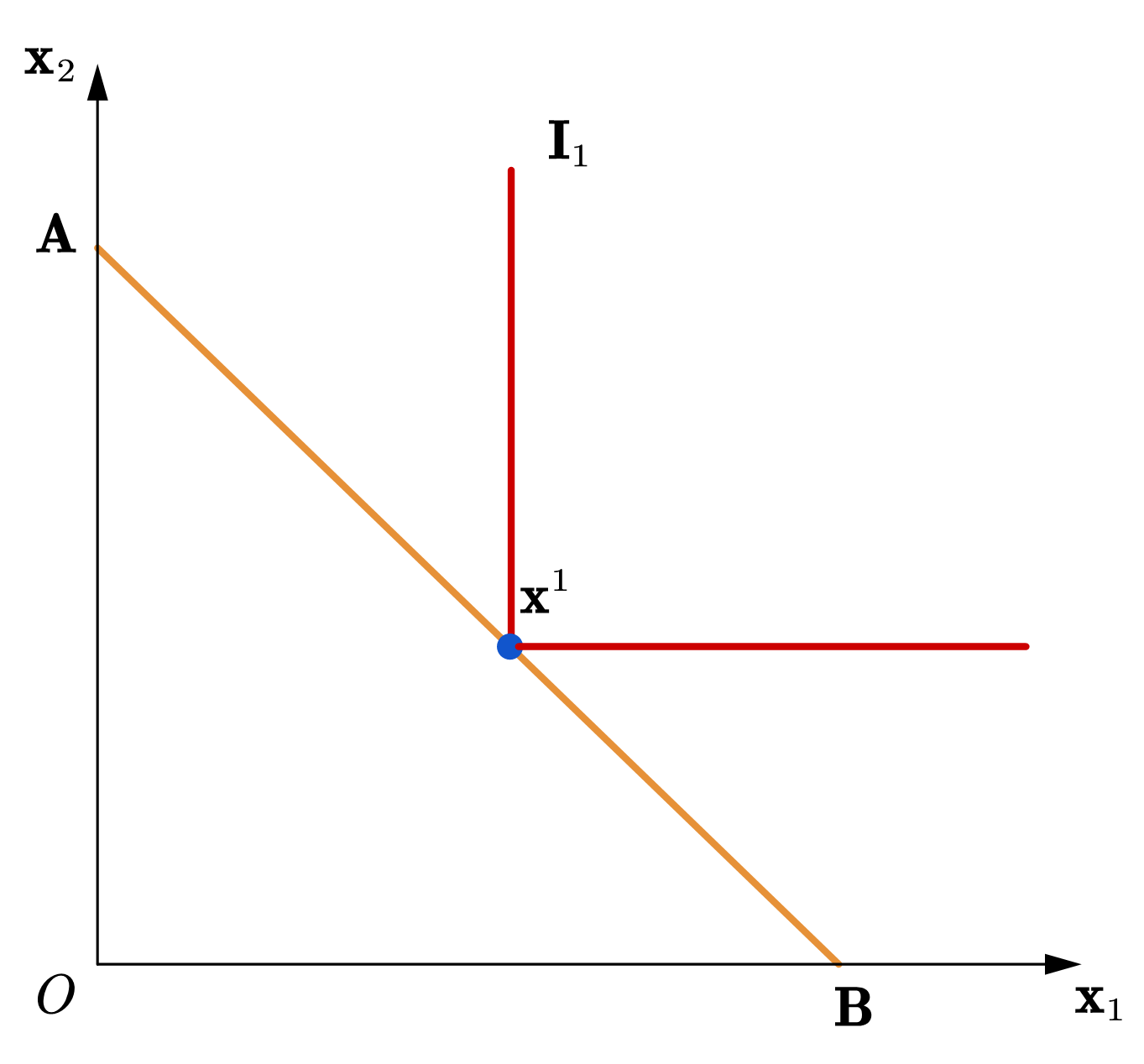
../../_images/ct-2-complete.png

Fig. 52 两商品为完全互补品时，消费者的最优选择为满足既定的互补比例。（黄色为预算线，红色为无差异曲线）#

假设，商品1和2的互补比例为\(a:b\)，效用函数为\(U = \max\{bx_1,ax_2\}\)。则最优选择满足：

\[\begin{split} \begin{array}{l} \frac{x_1^*}{x_2^*} = \frac{a}{b}\\ p_1x_1^* + p_2x_2^* = I\\ \Rightarrow x_1^* = \frac{aI}{ap_1 + bp_2}\quad x_2^* = \frac{bI}{ap_1 + bp_2} \end{array} \end{split}\]

对于完全替代品，我们可以先思考最简单的情况，假设两商品的边际替代率为1，说明它们在消费者眼中是等价的。既然两商品等价，那么自然是哪个商品便宜便购买哪个，如果它们的价格相等，则说明购买哪个，如何购买都无所谓，会有多个最优解[^l3-subs]。

下面我们做一个一般化的分析，假设两商品的替代比例为\(a:b\)（\(MRS_{12} = b/a\)），效用函数为\(U = bx_1 + ax_2\)。

  • 当\(MRS_{12} < p1/p2\) 时，消费者会将所有收入用于购买商品2，\(x_1^*=0, x_2^* = I/p_2\)。

  • 当\(MRS_{12} > p1/p2\) 时，增加商品1的数量会带来效用的增加，因为这个关系不会随商品数量的变化而改变，所以消费者会将所有收入用于购买商品1，\(x_1^*=I/p_1, x_2^* = 0\)。

  • 当\(MRS_{12} = p1/p2\)时， 消费者在预算线上调整商品1和2的数量，不会带来效用水平的变化，预算线上的所有消费束皆为最优选择，\(x_1^*=c, x_2^* = (I-p_1c)/p_2, c\in[0,I/p_1]\)

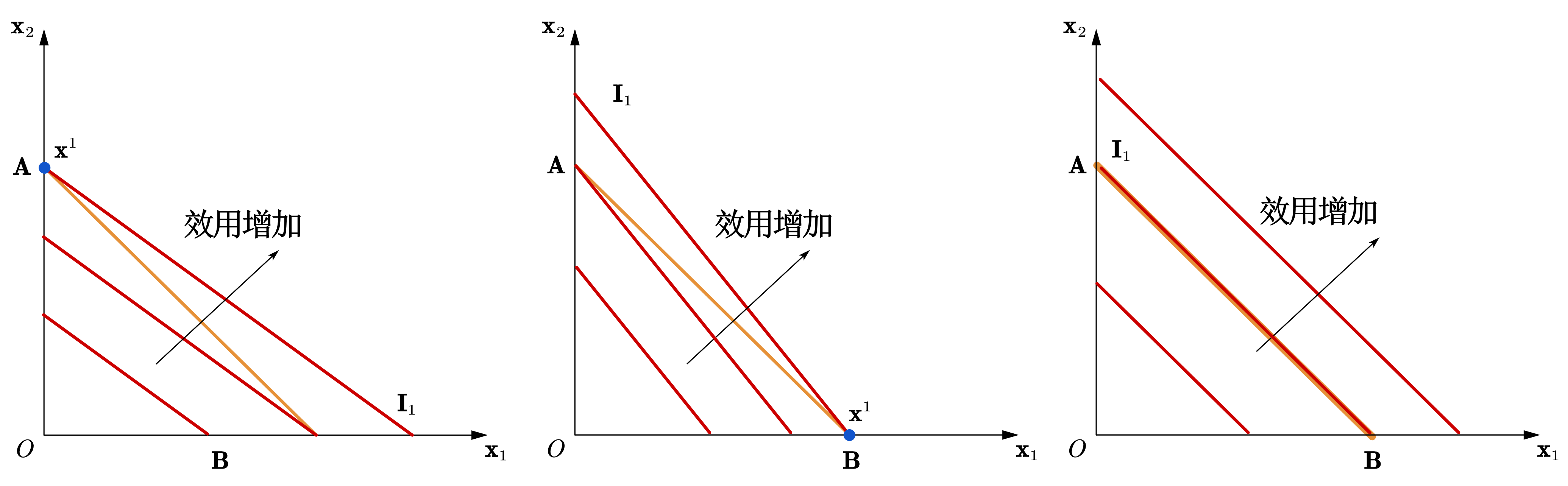
../../_images/ct-2-substitute.png

Fig. 53 两商品为完全替代品时，消费者的最优选择为选择单一商品消费或选择预算线上的任一商品组合。 （黄色为预算线，红色为无差异曲线）#