消费束、偏好和预算约束#

消费束 （Consumption Bundle or Comsumption Plan）#

「消费束」是所有商品的数量组合。假设有三种商品：巧克力，冰激凌和奶茶。包含这三种商品的「消费束」可一般化表述为\((x_1, x_2, x_3)\)，其中，\(x_1\)，\(x_2\)和\(x_3\)​为非负数，分别表示三种商品的数量。例如，

  • 消费束\(\mathbf{x}^1=(2, 1, 3)\)​表示商品组合含有2块巧克力，1个冰激凌和3杯奶茶

  • 消费束\(\mathbf{x}^2 =(0,3,1)\)​表示商品组合含有0块巧克力，3个冰激凌和1杯奶茶

消费束#

一个商品数量的集合。假设有n种商品，\(𝒙_i\)表示商品i的数量，则消费束可以表示为: \(\mathbf{x}=(𝒙_𝟏 ,𝒙_𝟐 , …， 𝒙_𝒏), \forall 𝒙_i\geq0\)

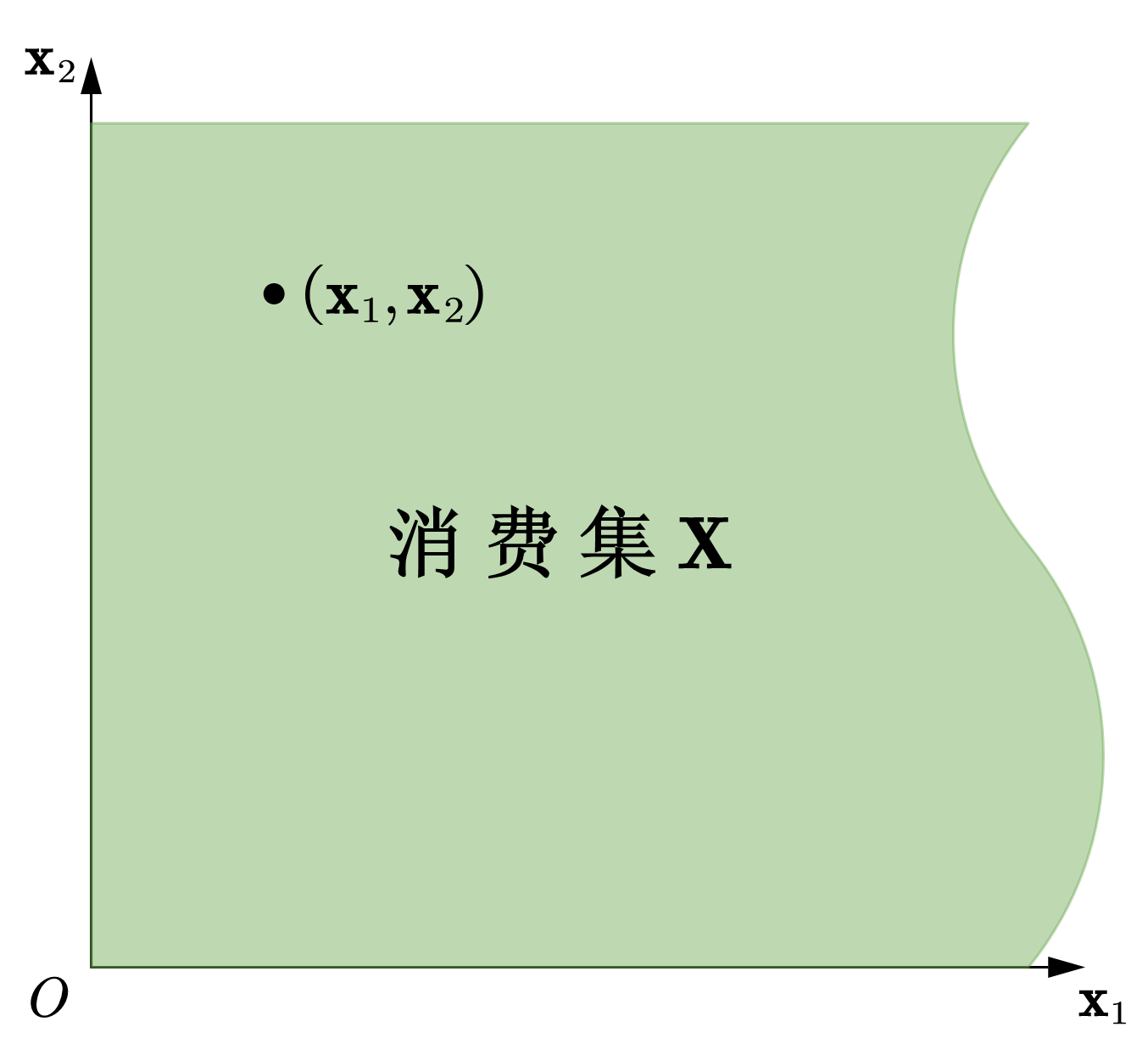
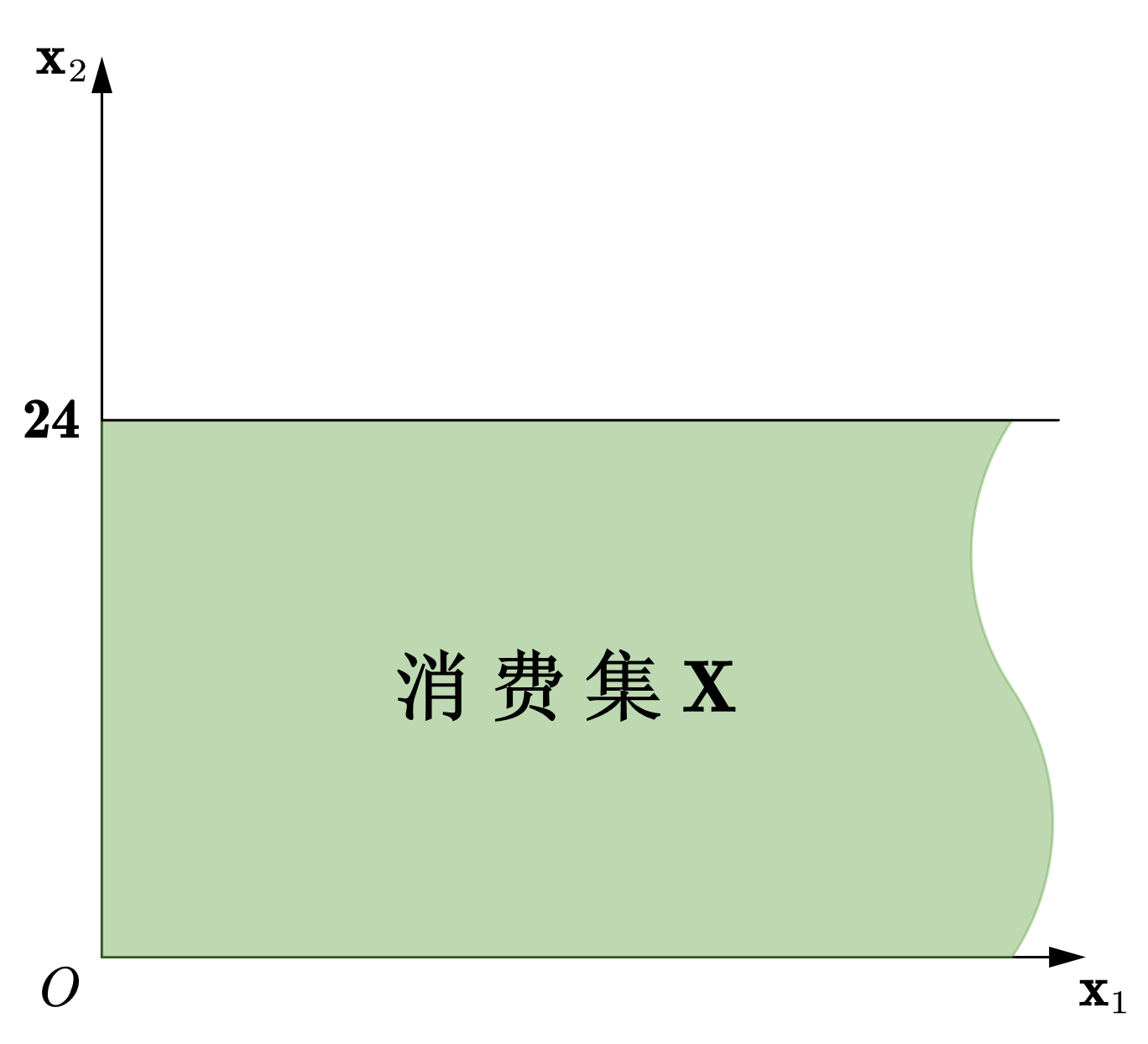
所有可能的消费束的集合称为消费集(Consumption Set), \(\mathbf{X}\)。消费集不受现实情况——比如收入——的约束，是消费者可以想象的所有可能的消费束的集合。假设有两种商品，商品1和2，其消费集通常设定为：\(\mathbf{X} = \mathbb{R}^2_+\)。因此，如图44(a)所示，在由这两种商品建立的坐标系内（习惯将商品1的数量画在横轴上），消费集对应的是第一象限（包括两坐标轴及原点），象限中的每一个点代表一个可能的消费束，这也暗含着假设所有商品数量都是无限可分的。

(a) 两种商品的消费集 (a) 两种商品的消费集
(b) 消费集受到总量约束 (b) 消费集受到总量约束

Fig. 44 消费集#

偏好 (Preference)#

什么是「偏好」？#

偏好描述的是消费者按个人喜好对所有消费束的排序。比方说，在\(\mathbf{x}^1\)，\(\mathbf{x}^2\)，\(\mathbf{x}^3\)，\(\mathbf{x}^4\)和\(\mathbf{x}^5\)五个消费束中，消费者小谢心中对它们的排序为：\(\mathbf{x}^1\)，\(\mathbf{x}^4\)，\(\mathbf{x}^3\)，\(\mathbf{x}^5\)，\(\mathbf{x}^2\) （假设没有喜好相同的消费束）。这个排序就代表了小谢的偏好：小谢最喜欢消费束\(\mathbf{x}^1\)，最不喜欢消费束\(\mathbf{x}^2\)；并且，与消费束\(\mathbf{x}^4\)相比，小谢更喜欢消费束\(\mathbf{x}^1\)，或者说\(\mathbf{x}^1\)给她带来的满足感更高。在此，更喜欢，满足感更高，更偏好，偏好更高和排序更高 这几个词的含义是等价的，在后面的部分会交替使用。

需要注意的是，偏好是一个主观概念，基于消费者的喜好或满足感。 不同人对相同的商品，或者同一商品在不同条件下，偏好是有可能不同的，即偏好因人、因时、因地而不同，如”中河失船，一壶千金，贵贱无常，时使物然”（ 《遏冠子·学问》）。

为了更好的描述和表示偏好，我们在消费集，\(\mathbf{X}\)，上定义了一个二元关系：\(\succsim\) （优于）。\(\succsim\)类似于\(\geq\)关系，表示两个消费束的一种排序关系，如果\(\mathbf{x}^1\succsim \mathbf{x}^2\)，表明消费者对\(\mathbf{x}^1\)的喜好程度不比\(\mathbf{x}^2\)差，即\(\mathbf{x}^1\)的排序要么和\(\mathbf{x}^2\)一样，要么比\(\mathbf{x}^2\)好。

接下来，我们需要给 \(\succsim\) 加上一些结构上的约束，以贴近消费者的选择特征，如排序具有一致性、喜好商品数量更多和更均衡的消费束。

理解\(\succsim\)：笛卡尔积和二元关系

  • 笛卡尔积：设A、B为集合，取A中元素作为第一元素，取B中元素作为第二元素构成有序对，所有这样的有序对所组成的集合，称为A和B的笛卡尔积，表示为\(A\times B\)，即

    \[ A\times B = \{(x,y)| x\in A, y\in B\} \]

    例如，\(A = \{x,y,z\}, B = \{4,18\}\), 可以计算\(A\times B, A\times A\)和\(B\times B\)为：

    \[\begin{split} \begin{eqnarray*} A\times B &=& \{(x,4), (x,18),(y,4),(y,18),(z,4),(z,18)\}\\ A\times A & =& \{(x,x),(x,y),(x,z),(y,x),(y,y),(y,z),(z,x),(z,y),(z,z)\} \\B \times B & =& \{(4,4),(4,18),(18,4),(18,18)\} \end{eqnarray*} \end{split}\]

  • 二元关系：如果一个集合的元素都是有序对，则称该集合为一个二元关系，记作\(R\)。二元关系可简称为关系。对于二元关系\(R\)，如果有序对\((a,b)\in R\), 称a和b具有R关系，记作 \(aRb\)；如果\((a,b)\notin R\)，称a和b没有R关系，记作 \(a\not{R}b\)

  • 设A、B为集合，\(A\times B\)的任意一个子集是集合A到B的一个二元关系。当\(A =B\)时，称为定义在A上的二元关系。

    如上例所示， 集合\(R_1 = \{(x,4), (y,4),(y,18),(z,4)\}\subset A\times B\)是从A到B的一个二元关系；集合\(R_2 = \{(x,x),(y,y),(z,z)\}\subset A\times A\) 是A上的一个二元关系。

因此，\(\succsim\)代表的是一个集合：在消费集内，所有满足 \(\succsim\) 的消费束对，如\((\mathbf{x}^1, \mathbf{x}^2)\)满足消费者对\(\mathbf{x}^1\)喜好程度不比\(\mathbf{x}^2\)差，所构成的集合：

\[ \succsim = \{(\mathbf{x}^1,\mathbf{x}^2)|\mathbf{x}^1\in X, \mathbf{x}^2\in X, 对\mathbf{x}^1的喜好程度不比\mathbf{x}^2差 \} \subset X \times X \]

若\((\mathbf{x}^1,\mathbf{x}^2)\in \succsim\)，可记为 \(\mathbf{x}^1\succsim \mathbf{x}^2\)。

\(\succsim\) 的基本假设#

假设1：完备性或可比性（Completeness）。对于任意两个消费束，\(\mathbf{x}^1\)和\( \mathbf{x}^2\)，可以得到 \(\mathbf{x}^1\succsim \mathbf{x}^2\), 或\(\mathbf{x}^2\succsim \mathbf{x}^1\)，或两者同时成立。该假设确保消费者能够判断自己喜欢什么。

假设2：传递性（Transitivity）。对于消费束，\(\mathbf{x}^1\)，\(\mathbf{x}^2\)和\( \mathbf{x}^3\)，如果\(\mathbf{x}^1\succsim \mathbf{x}^2\) 且 \(\mathbf{x}^2 \succsim \mathbf{x}^3\)，则 \(\mathbf{x}^1 \succsim \mathbf{x}^3\)。该假设确保消费者可以做出一致性的选择——前后一致的排列所有消费束，避免出现排序循环的情况，如\(\mathbf{x}^1\succsim \mathbf{x}^2\) ， \(\mathbf{x}^2 \succsim \mathbf{x}^3\)，却有 \(\mathbf{x}^3 \succsim \mathbf{x}^1\)。

有些书上也假设 \(\succsim\) 具有自反性（Reflectivity），即任何一个消费束都可与自身比较，即\(\mathbf{x}\succsim \mathbf{x}\)。因为一个消费束的排序肯定不会比自身差，所以，我们省略了此假设。

如果\(\succsim\)满足假设1和2，则将此关系称为偏好关系。相应的，\(\mathbf{x}^1\succsim \mathbf{x}^2\)称作消费束\(\mathbf{x}^1\)（弱）偏好于消费束\(\mathbf{x}^2\)。在此基础上，我们还可以定义严格偏好关系 和 无差异关系。 并且，可以证明这两个关系都具有传递性。

  • 如果\(\mathbf{x}^1\succsim \mathbf{x}^2\) 且 \(\mathbf{x}^2\succsim \mathbf{x}^1\)，则说明在消费者心里，消费束\(\mathbf{x}^1\)至少和\(\mathbf{x}^2\)一样好，\(\mathbf{x}^2\)也至少和\(\mathbf{x}^1\)一样好，那么，\(\mathbf{x}^1\)和\(\mathbf{x}^2\)的排序或喜好程度一定是一样的，称为\(\mathbf{x}^1\)与\(\mathbf{x}^2\) 无差异，记为\(\mathbf{x}^1\sim \mathbf{x}^2\)。需要注意的是「无差异」指的是喜好程度的无差异，而不是数量的无差异。

  • 如果\(\mathbf{x}^1\succsim \mathbf{x}^2\) 且 \(\mathbf{x}^2\nsucceq \mathbf{x}^1\) ，则说明在消费者心里，消费束\(\mathbf{x}^1\)至少和\(\mathbf{x}^2\)一样好，同时，\(\mathbf{x}^2\)排序比\(\mathbf{x}^1\)差，那么，\(\mathbf{x}^1\)一定排在\(\mathbf{x}^2\)的前面，或者说消费者更偏好消费束\(\mathbf{x}^1\)，称为 \(\mathbf{x}^1\)严格偏好于\(\mathbf{x}^2\)，记为\(\mathbf{x}^1 \succ \mathbf{x}^2\) 。

假设1和2说明我们可以将消费集分割为三部分，比如，给定某一个消费束\(\mathbf{x}\)，可以找到严格偏好于、无差异以及严格差于\(\mathbf{x}\)的消费束的集合，如图45所示。很显然，完备性和传递性并未告诉我们具体应如何分割，因此，分割有很大程度的任意性，比如，与\(\mathbf{x}\)无差异的消费束集合可以是开集，消费束中商品的数量增加仍与原消费束无差异——这显然与稀缺性假设相矛盾。 这说明，我们还需要对偏好关系进一步约束，使其具有更恰当的结构。

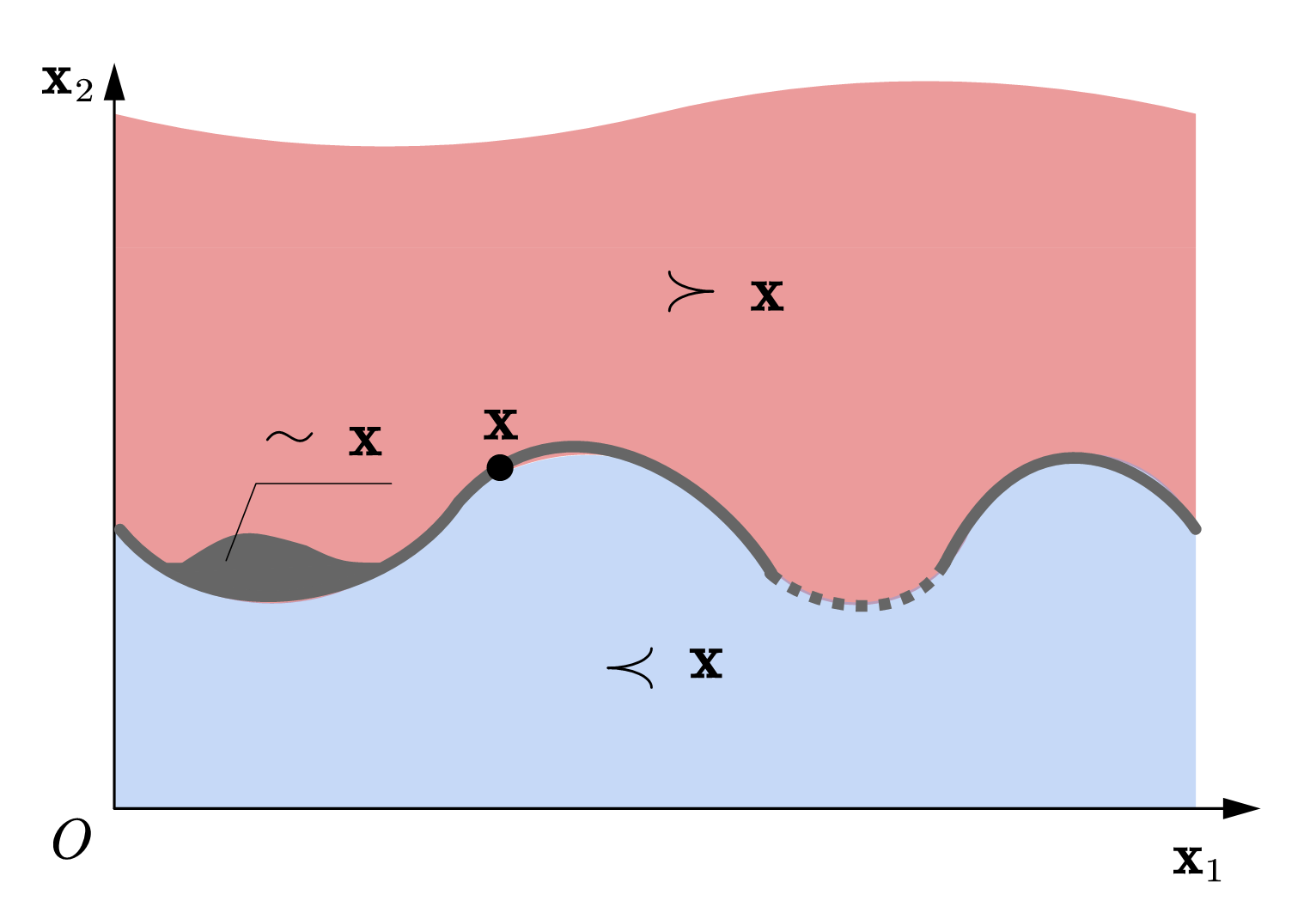
../../_images/ct-1-consumption-set-split.png

Fig. 45 基于完备性和传递性假设，对消费集的一个可能的分割#

假设3：连续性。对于任意两个消费束序列 \(\{(\mathbf{x}^n, \mathbf{y}^n)\}_{n=1}^\infty\), 如果\(\forall n\geq 1\), 都有\(x^n\succsim y^n\), 且

\(lim_{n\rightarrow \infty} \mathbf{x}^n =\mathbf{x}\)，\(\quad lim_{n\rightarrow \infty} \mathbf{y}^n =\mathbf{y}\)，那么, \(\mathbf{x}\succsim \mathbf{y}\)。该假设含义着消费束之间的偏好关系不会发生突变。我们也可以这样理解，对于任意消费束\(\mathbf{x}\)，与之无差异的消费束所构成的集合为闭集[^l3-cts]，该假设主要是从数学的角度添加的约束。【加图】

假设4：严格单调性（Strictly Monotonicity）。如果消费束\(\mathbf{x}^1\)中的商品数量都大于等于消费束\(\mathbf{x}^2\)中所对应的商品数量，且至少有一种商品不等号严格成立，如\(\mathbf{x}^1=(3,4,3)\)，\(\mathbf{x}^2=(3,1,3)\)，则\(\mathbf{x}^1\)严格偏好于\(\mathbf{x}^2\)（\(\mathbf{x}^1\succ \mathbf{x}^2\)) 。该假设可以理解为是对「经济物品」含义的反映——“有胜于无且多胜于好”。说明，对于任意消费束\(\mathbf{x}\)，与之无差异的消费束集合不会有带状区域，也不会向右上方倾斜，我们将该集合的连线称为无差异曲线。【加图】

假设5：严格凸性（Strictly Convexity）。对于任意两个消费束\(\mathbf{x}^1, \mathbf{x}^2\) 如果\(\mathbf{x}^1\neq \mathbf{x}^2\), 且 \(\mathbf{x}^1\succsim \mathbf{x}^2\), 那么

\[ t\mathbf{x}^1 + (1-t)\mathbf{x}^2 \succ \mathbf{x}^2 \quad \forall t\in[0,1]。\]

假设\(\mathbf{x}^1=(x^1_1, x^2_2)\), \(\mathbf{x}^2=(x^2_1, x^2_2)\), 则 \(t\mathbf{x}^1 + (1-t)\mathbf{x}^2\) 代表的是两个消费束的凸组合，其所对应的消费束为\((tx_1^1 + (1-t)x_1^2, tx_2^1 + (1-t)x_2^2)\)

该假设含义着消费者喜欢多样性。比如，在某条无差异曲线上，小谢对两个数量差异比较大的消费束\((1,20)\)和\((25,3)\)偏好相同，再假设我们将这两个消费束中的商品数量平衡一下，比如，令 \(t = 0.5\)，得到消费束\((13,11.5)\)，严格凸性假设含义着这个均衡后的消费束会严格偏好于商品数量极端的消费束，即\((13,11.5)\succ (1,20)\) 或 \((13,11.5)\succ (20,3)\)。更一般而言，将无差异曲线上的两点相连，其连线一定在该无差异曲线的右侧，这说明无差异曲线一定是严格凸向原点的，或者，对于任意消费束\(\mathbf{x}\)，集合\(\{\mathbf{x}'| \mathbf{x}’ \succsim \mathbf{x}\}\)（包含无差异曲线及其右侧的所有消费束）为严格凸集。

消费者喜欢商品的多样性

假设有两种商品，基于严格单调假设，无差异曲线必然向右下方倾斜，所以与消费束\(\mathbf{x}\)无差异的消费束中两商品的数量必然是一增一减变化，而不会是同增或同减，如\((1,20)\sim (25,3)\)。因此，在两个无差异的消费束的凸组合中，两商品的数量会更均衡。

无差异曲线（Indifference Curve, IC）#

当有两种商品时，我们可以用几何的方式表示偏好，对应的概念为无差异曲线。

无差异曲线#

在消费集中，对于某个消费束\(\mathbf{x}\)，将与之无差异（\(\sim\)）的所有消费束连接起来所构成的曲线，也可称为「等优曲线」。 消费者对同一条无差异曲线上的消费束的偏好程度都是一样的。

在消费集中，无差异曲线有无数条，偏好关系对应的是所有无差异曲线的集合(indifference map)。

现实中可选择的商品有很多种，为什么我们通常会选择两种商品进行分析呢？

之所以选择两种商品进行分析，一是因为易于表达，如，三种商品需要构建三维图，二是因为两种商品的选择需要涉及代价方面的权衡，而一种商品不用，可以说，二与一有大不同，但二与三或者更多却相差不大——两种商品选择的结论适用于更多商品。在最优选择部分，会看到从两种商品选择的最优条件扩展到多种商品。

基于偏好关系的基本假设，无差异曲线有如下四个特征：

  • 特征1： 无差异曲线必然向右下方倾斜，即斜率为负。

    特征1源于严格单调假设，因为如果既要增加一种商品的数量，还要保持与原消费束无差异，则另一种商品的数量必然需要减少，否则新的消费束会严格优于原消费束。无差异曲线只能沿着两种物品一增一减的方向移动。

  • 特征2：在同一坐标平面上，任何两条无差异曲线都不会相交。

    对于特征2，我们可以使用反证法证明。如图46所示，假设两条无差异曲线相交，交点为消费束\(x^1\)。

    首先，在两条无差异曲线上，我们可以找到两个消费束，满足一个消费束中的商品数量都严格大于另一个消费束中的商品数量，如\(x^2\)和\(x^3\)，单调性假设表明\(x^3\)严格偏好于\(x^2\)。

    其次，\(x^3\)和\(x^1\)，\(x^2\)和\(x^1\)分别在同一条无差异曲线上，这表明，\(x^3\)和\(x^1\)无差异，\(x^2\)和\(x^1\)无差异，基于传递性假设，\(x^3\)和\(x^2\)无差异。但是，此结论与\(x^3\)严格偏好于\(x^2\)矛盾。

    因此，任意两条无差异曲线都不会相交。

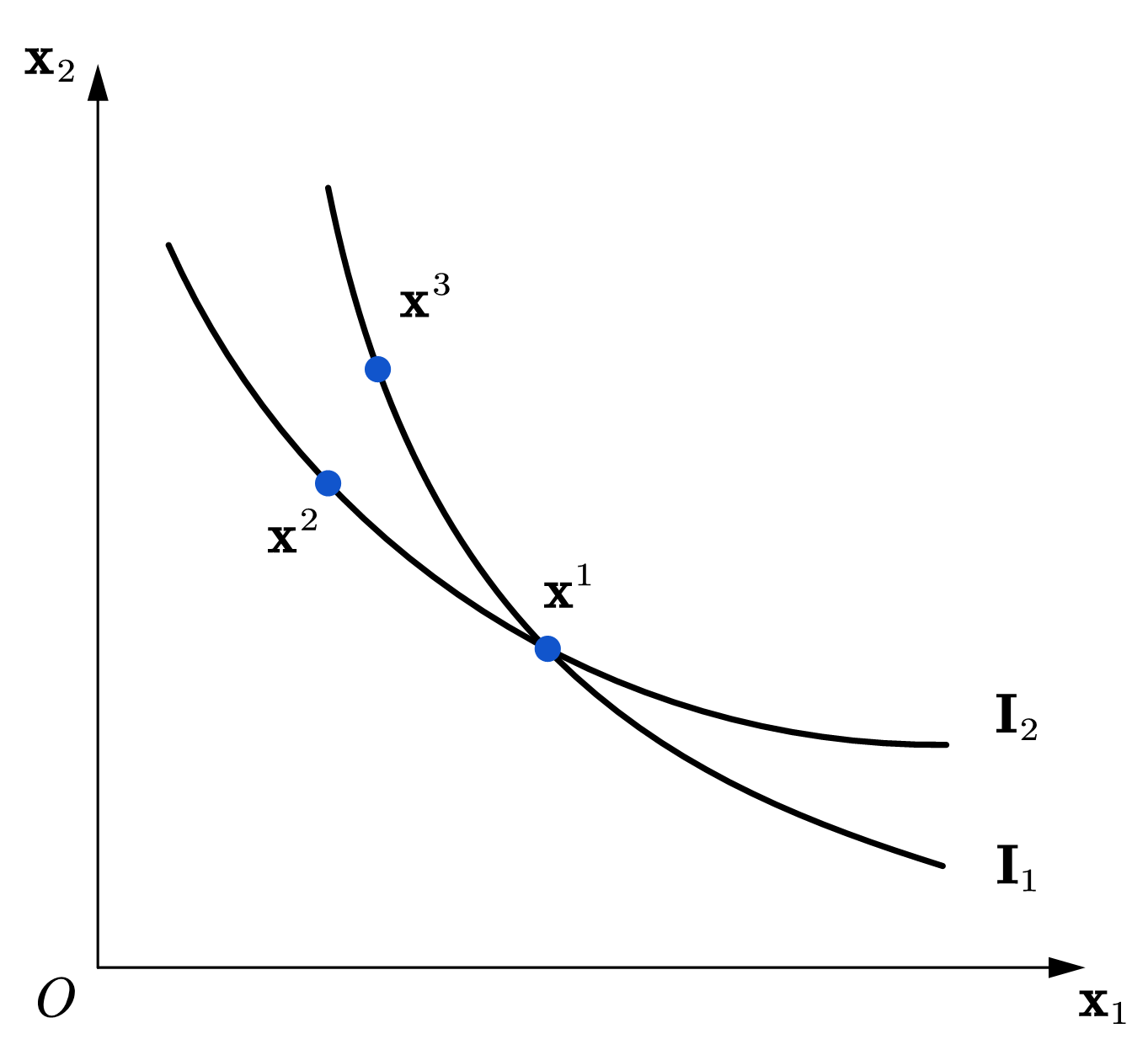
../../_images/ct-1-indifference-curve-cross.png

Fig. 46 无差异曲线相较可以推出矛盾。#

  • 特征3：在消费集内，每个消费束都会有一条无差异曲线通过，换言之，在任何两条无差异曲线之间，可以有无数条无差异曲线。如果将所有的无差异曲线都画出来，消费集会被完全填满。并且，无差异曲线离原点越远，其对应的偏好程度越高（严格单调假设）。

  • 特征4：无差异曲线严格凸向原点（严格凸性假设）。

我们将具有上述四个特征的无差异曲线称为性状良好的无差异曲线。

如图47所示，严格凸向原点含义着在同一条无差异曲线上，随着商品1数量的增加，无差异曲线的切线变的越来越平坦，表明消费者愿意放弃的商品2的数量会越来越少。为了描述这一特征，我们定义了一个概念：边际替代率。

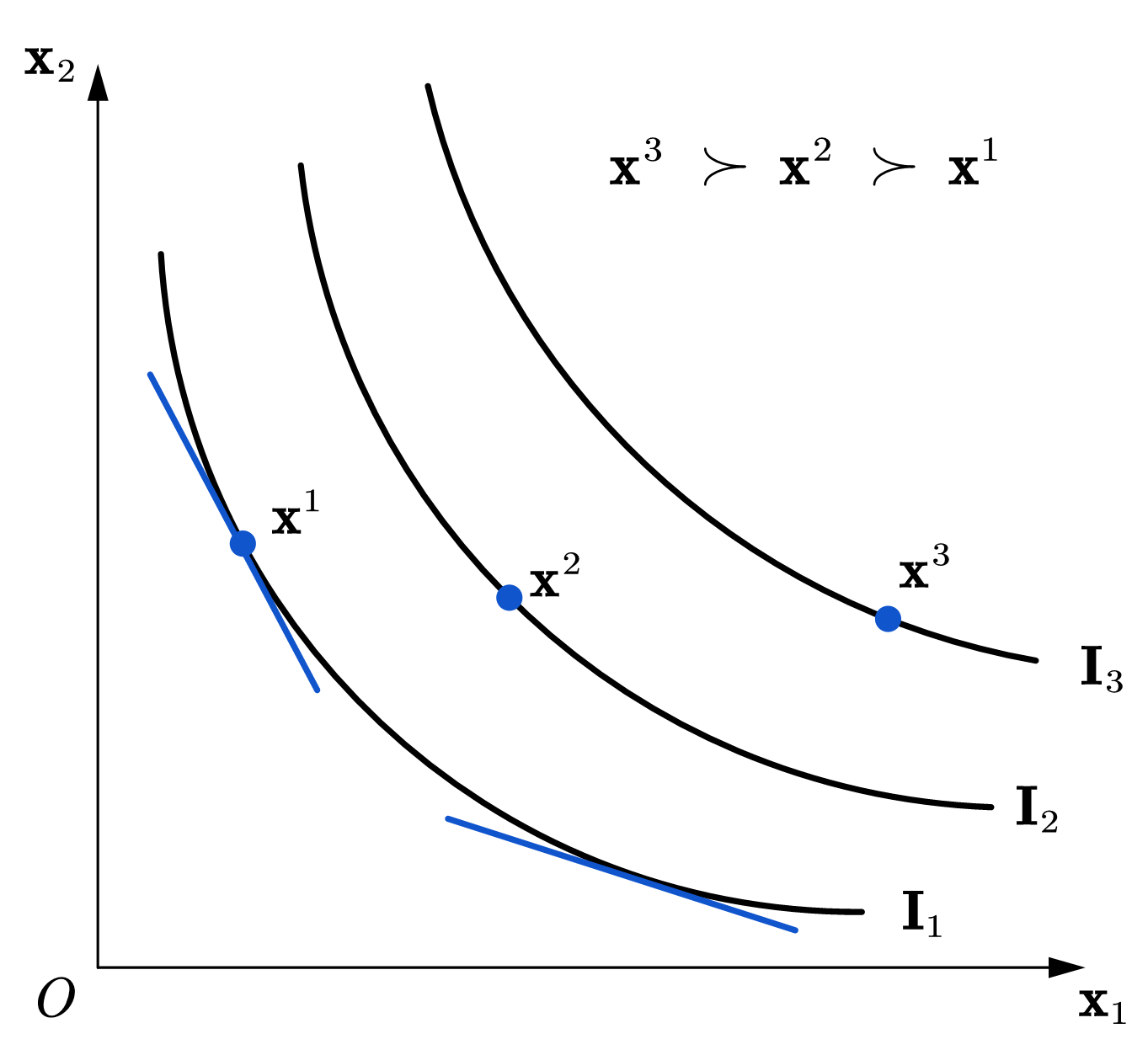
../../_images/ct-1-indifference-curve.png

Fig. 47 无差异曲线#

边际替代率 （Marginal Rate of Substitution, MRS）#

在同一条无差异曲线上，我们将增加一单位商品1所愿意放弃的商品2的数量定义为商品1对商品2的边际替代率。例如，在消费束\(x^* =(x_1^*,x_2^*)\) 处，商品1对商品2的边际替代率（\(MRS_{12}\)）可以表示为：

\[ MRS_{12}=lim_{\Delta x_1\rightarrow 0}-\frac{\Delta x_2}{\Delta x_1}|_{x^*,\sim}=-\frac{d x_2}{d x_1}|_{x^*,\sim} \]

因为边际替代率被定义为正值，且\(x_1\)和\(x_2\)在同一条无差异曲线上的变化方向相反，所以上式中要加上负号。更一般而言，商品1对商品2的边际替代率（\(MRS_{12}\)）为:

\[ MRS_{12}=-\frac{d x_2}{d x_1}|_{x^*,\sim} \]

商品1对商品2的边际替代率描述了两商品在消费者心中的替换关系，或者也可以理解为，在偏好程度不变的前提下，为获得商品1，消费者愿意付出的用商品2表示的心理代价。边际替代率的几何含义为无差异曲线在给定消费束处的切线的斜率的绝对值（注意：商品1在横轴上）。

边际替代率递减规律#

如图47所示，无差异曲线严格凸向原点表明，随着商品1（横轴商品）数量的增加，商品1对商品2的边际替代率递减，或者说消费者为获得商品1所愿意付出的（商品2的）代价是递减的。我们将此特征称为边际替代率递减规律：

\[ \frac{d MRS_{12}}{dx_1} < 0 \]

严格凸性假设含义着消费者喜欢「多样性」，因此，当某种商品的数量不断增加时，该商品在消费者眼中的重要性会不断下降，所以，消费者愿意为其付出的单位代价会不断降低。

边际替代率（Marginal Rate of Substitution, MRS）#

在同一条无差异曲线上，增加一单位商品（如商品1）所愿意放弃的另一种商品（如商品2）的数量称为两种商品（商品1对商品2）的边际替代率。

边际替代率也可以理解为，在同一条无差异曲线上，减少一单位商品所愿意获得另一种商品的补偿，但通常，我们会从增加的角度去看，下面所说边际替代率递减也是如此。

效用函数#

接下来，我们学习用代数的方式表示偏好，这便需要引入效用的概念。

效用#

效用是武断地以数字排列选择的随意定名。如何理解这个定义呢？

首先，依据偏好，我们可以给每个消费束赋予一个数值，赋值方式满足如下条件：

  • 数值相同代表消费束无差异，或在同一条无差异曲线上；

  • 数值越大代表排序越高或满足度越高，即数值高的消费束严格优于数值低的消费束。

如是，便将偏好便转化为了数字排序。

其次，我们给这些数值起一个名字，称为效用。因此，消费束效用高代表赋值高，等价于消费束在消费者心中排序高或更偏好；相应的，效用低代表赋值低，等价于消费束在消费者心中排序低或不偏好。

效用#

武断地以数字排列选择的随意定名，用以解释人的选择行为。

效用的历史

效用这个词源自边沁（Jeremy Bentham, 1748-1832，英国哲学家），他提出了”功利/功用主义”（Utilitarianism）的哲学思想（功利主义即是效用主义）。边沁认为人们选择的动机都可以归结为追求愉悦（pleasure）和避免痛苦（pain），因此，他将选择的目标简化为最大化人们的愉悦（pleasure）或幸福，并称之为效用原则。但在效用原则中，仅考虑一个行为的结果对最大愉悦值的影响——能增加最大快乐值的即认为是善；反之即为恶。不考虑行为的动机与手段。

为了评估愉悦，边沁给出了量化衡量愉悦的标准——同一件事对人们的愉悦感都是一样的。边沁认为只要每个人真正的追求自己的最大幸福，结果必将是最大多数人的最大幸福，但是，（1） 愉悦是心理，是主观的，本质上其实是无法被度量的——“直接地或从本身来衡量欲望，或是由欲望的实现而产生的满足，即使不是不可想象的，也是不可能的，我们对这一点不能过于坚持”（马歇尔《经济学原理》）。（2）个人实际上追求的幸福不等于值得追求的幸福。（3）个人实际上追求的幸福不等于公众的幸福。

虽然在效用引入经济学之初有量化度量心理的含义，但是现在效用仅仅是对偏好的一个武断定名，与心理的度量已毫无关系，如果不叫效用，改为任何其它的称呼也不会影响我们的分析。如史托斯（R.H.Strotz）所言：”很明显，我们无须判断效用的量度是以金钱，或以散漫的时日，或以八度和音，或以英寸来支持，而我们更无须认为效用的量度是一个心理上的单位。” check 来源

对于同一偏好，我们可以采用不同的效用体系（赋予不同的效用值）去表述，只要消费束的排序相同即可；反之，如果在不同的效用体系下，所有消费束的排序都相同，那么说明这些效用体系代表了同一个偏好。如在下面所列的三种赋值方式中，消费束\(\mathbf{x}^1\)，\(\mathbf{x}^2\)和\(\mathbf{x}^3\)被赋予了不同的效用值，虽然效用不同，但是都代表\(\mathbf{x}^1\)严格优于\(\mathbf{x}^2\)，\(\mathbf{x}^2\)严格优于\(\mathbf{x}^3\)，因此都属于同一偏好。

  • 赋值1：\(\mathbf{x}^1\)，\(\mathbf{x}^2\)和\(\mathbf{x}^3\)的效用分别为20，10，5

  • 赋值2：\(\mathbf{x}^1\)，\(\mathbf{x}^2\)和\(\mathbf{x}^3\)的效用分别为40，20，10

  • 赋值3：\(\mathbf{x}^1\)，\(\mathbf{x}^2\)和\(\mathbf{x}^3\)的效用分别为28，14，7

这也说明对于效用，有意义的是数值之间的相对大小关系，而非数值的绝对量和它们之间的差异。喜好可以排序但无法度量，我们不能说两个效用为5的消费束所带来的满足感与效用为10的消费束是等价的，或者效用为10的消费束与效用为2的消费束的满足感之差恰等于效用为8的消费束（我们可以自己设定不同的消费束去进行思考）。 因此，效用是序数的，而非基数—–赋予效用的数值只有排序的意义（序数），不能进行加减乘除四则运算（基数）。

Note

效用是序数的，而非基数。

效用函数#

我们可以将赋予消费束效用值的过程看做是消费束到效用值的映射，这说明，它们之间的关系可以用一个函数来描述，如

\[ U=u(x_1,x_2,…,x_n) \]

其中，\((x_1,x_2,...,x_n)\)为消费束，U为效用值，这个函数被称为**「效用函数」**。例如，\(U=x_1x_2\)是一个可能的效用函数。

基于效用函数，在某一条无差异曲线上的消费束中商品的数量关系应满足：

\[ \bar{U}=u(x_1,x_2) \]

其中，\(\bar{U}\)是给定的效用水平。相应的，无差异曲线的表达式可以写为

\[ x_2 = u^{-1}(\bar{U},x_1) \]

效用的序数性表明对效用函数做「单调递增变化」仍表示同一偏好，因为单调递增变化不会影响消费束的排序。简言之，同一个偏好可以由不同的效用体系赋值，对应不同的效用函数，只要它们所对应的消费束的排序一致即可。

单调递增变化

  • 假设f是一个单调递增变化，那么，如果\(u(x_1,x_2)>u(y_1,y_2)\), 则\(f(u(x_1,x_2))>f(u(y_1,y_2))\)。

  • 几种单调递增变换:

    • 乘上一个正数，比如，\(u(x_1,x_2)*10\)

    • 加上任意一个数，\(u(x_1,x_2)+5\)

    • 奇次方, \(u(x_1,x_2)^3\) （如果函数值为非负，则也可以取偶次方）

    • 取对数或以e为底 \(\log(u(x_1,x_2))\) 或 \(e^{u(x_1,x_2)}\)

考考你

下列选项中，哪一个效用函数不属于同一个偏好？（ ）

A. \(\quad U=x_1^a x_2^b, \quad 0<a,b<1\)

B. \(\quad U=k(alogx_1 + blogx_2)^5, \quad 0<a,b<1, k<0\)

C. \(\quad U=ax_1 + blogx_2,\quad 0<a,b<1\)

D. \(\quad U = e^{x_1^a x_2^b},\quad 0<a,b<1\)

边际效用（Marginal Utility, MU）#

边际效用是指当某种商品的数量变化一单位时，所引起的效用水平的变化。如果效用函数\(U=u(x_1,x_2)\)处处可微，则商品1和2的边际效用可以用效用函数对商品数量的偏导表示：

(3)#\[\begin{eqnarray} MU_1 &=& \frac{\partial u(x_1,x_2)}{\partial x_1} >0 \\ MU_2 &=& \frac{\partial u(x_1,x_2)}{\partial x_2} >0 \end{eqnarray}\]

在计算边际效用时，其它商品的数量需要保持不变，并且，由严格单调假设可知，边际效用严格为正。在效用不变的前提下，我们可以推出边际效用与边际替代率之间的关系：

\[ MRS_{12} = \frac{MU_1}{MU_2} \]

证明: \(MRS_{12} = \frac{MU_1}{MU_2}\)

  • 在同一条无差异曲线上（假设效用值为\(\bar{U}\)）的消费束满足

\[ \bar{U} = u(x_1,x_2) \quad \quad (p.1) \]

  • 对(p.1)做全微分，因为效用不变，所以\(d\bar{U}=0\)，可得边际替代率等于两商品的边际效用之比

\[\begin{split} \begin{array}{ll} &d\bar{U} = \frac{\partial u}{\partial x_1}dx_1 + \frac{\partial u}{\partial x_2}dx_2\\ \Rightarrow & 0=\frac{\partial u}{\partial x_1}dx_1 + \frac{\partial u}{\partial x_2}dx_2 = MU_1dx_1 + MU_2dx_2 \\ \Rightarrow & MRS_{12} = \frac{MU_1}{MU_2} \end{array} \end{split}\]

边际效用递减规律#

边际效用递减规律是指在一定时间内，每增加一单位商品所能增加的效用单位（边际效用），即多消费一单位该商品所增加的满足度，是递减的，即，

\[\begin{split} \frac{\partial^2 U}{\partial x_1^2}= \frac{\partial MU_1}{\partial x_1}<0\\ \frac{\partial^2 U}{\partial x_2^2}= \frac{\partial MU_2}{\partial x_2}<0 \end{split}\]

假设我们感到口渴，喝下第一杯水时感觉非常舒服，第二杯感觉还行，第三杯没什么感觉了，喝到第四杯可能就会觉得不再需要了。同样地，当我们初次接触某件事物时，可能会因为新鲜感而觉得很有意思，但是随着接触的频率增加，它的新鲜感会逐渐减退，同时我们从中获得的满足感也会逐渐下降。这些便是际效用递减规律的体现：当消费者不断地增加某种商品的数量时，他们满足感的增幅是会随之下降的。

需要注意的是，边际效用递减是以偏好不变为前提的。如马歇尔所言：“在这一规律（边际效用递减规律）中有一个暗含的条件，应当加以说明。就是，我们假定，不容许这期间有时间使消费者自己在性格上和爱好上发生任何变化。所以，这规律没有这些例外。一个人越多听优美的音乐，他对音乐的爱好就越强烈。贪婪和野心往往是不会满足的；或者，高尚的美德和酗酒的恶习同样愈演愈烈。这是因为我们的观察基于若干时期，而且被观察的人在这个时期的开始与结束，具有不同的性格或爱好。我们如果当一个人就是像他现在这样，而不容许有时间让他的性格发生任何变化，那么，一物对他的边际效用，就会随着这件东西的供给的每一次增加而不断递减”。（马歇尔《经济学原理》）。

边际效用递减 v.s. 边际替代率递减#

需要注意的是，边际效用递减与边际替代率递减是两个概念，并不是相互推出的关系。我们看这样一个例子，假设效用函数为\(U=x_1x_2\)， 两商品的边际替代率为：\(MRS_{12} = \frac{x_2}{x_1}\) ，显然， 随着商品1的数量增加，\(MRS_{12}\)递减，满足边际替代率递减规律。但是，两商品的边际效用分别为\(MU_1 = x_2\), \(MU_2=x_1\), 皆为定值，不满足边际效用递减规律。

更形象的理解是，\(MRS\)约束的是消费束在同一条无差异曲线上的替换关系，而边际效用约束的是消费束跨无差异曲线（单独增加一种商品的数量）的喜好（效用）的变化，两者并没有必然的联系。如图48所示，凹向原点的无差异曲线是可以边际效用递减的；凸向原点的无差异曲线也是可以是边际效用不变或递增的。边际效用递减与边际替代率递减无关的证明见附录。

因此，边际效用递减是对效用函数的额外约束，不能由偏好关系的基本假设推出。在消费者理论中推出消费者的最优选择其实是不需要边际效用递减规律的。

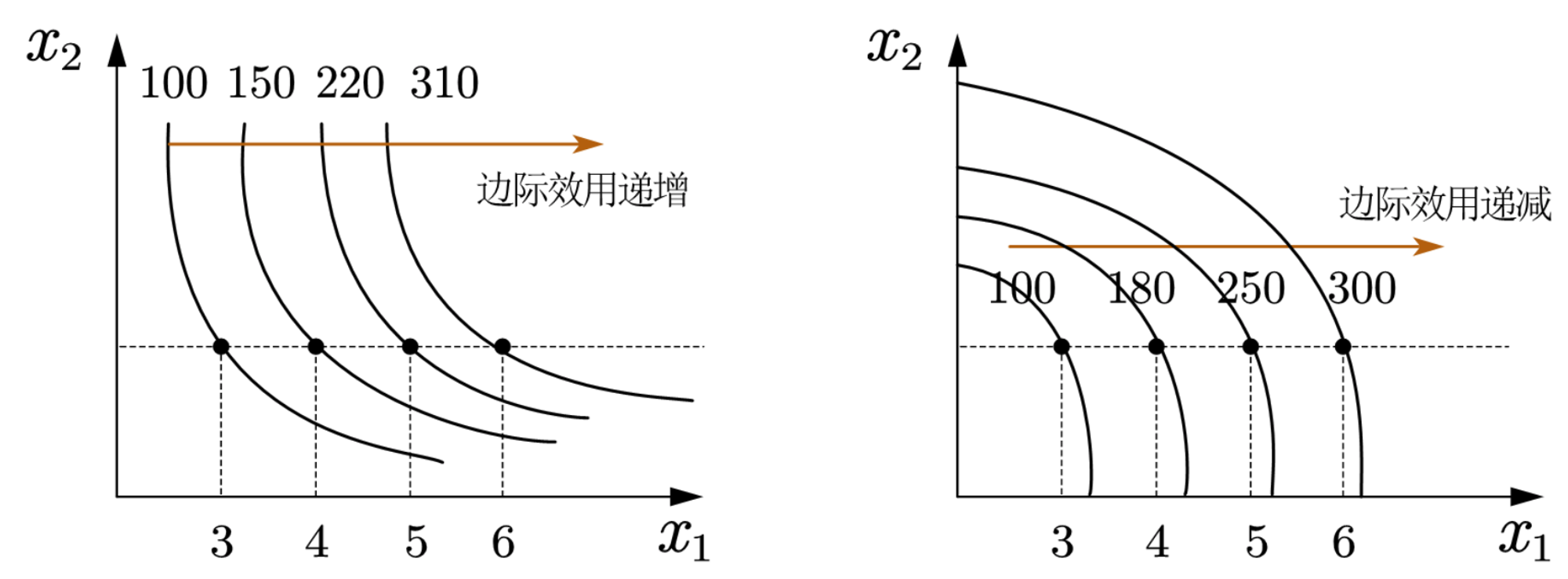
../../_images/ct-1-mrs-mu.png

Fig. 48 边际替代率递减和边际效用递减规律不是相互推出的关系。#

总结#

为了研究消费者的选择，我们引入了偏好的概念。偏好是消费者依据其喜好对所有消费束（商品的数量组合）的排序。为了描述偏好，在消费集上，我们定义了偏好关系，\(\succsim\)，由偏好关系可以定义无差异和严格偏好关系。偏好关系满足5个基本假设：完备性、传递性、连续性、严格单调性和严格凸性。完备性和传递性确保消费者可以一致的排列所有消费束，连续性确保偏好关系不会发生突变，严格单调性反映的是经济物品的含义，严格凸性表明消费者喜欢“多样性”。

偏好可以由无差异曲线集合和效用函数表示。它们都受到偏好基本假设的约束。无差异曲线是具有相同效用的消费束的连线。在无差异曲线上，我们定义了边际替代率（MRS），严格凸性表明边际替代率递减。效用函数是描述消费束和效用关系的函数。效用是对消费束的赋值，效用值的高低代表消费者偏好程度的高低，因此，效用是序数的，对效用函数的单调递增变化仍表示同一偏好。基于效用函数，我们定义了边际效用，其具有边际效用递减的特征。需要记住，效用的序数特征表明效用和边际效用的数值本身是没有任何意义的。

两种特殊性状的无差异曲线：完全替代品和互补品#

完全替代品#

如果在消费者眼中，a个商品1永远等价于b个商品2，即商品1对商品2的边际替代率为定值（\(MRS_{12}=\frac{b}{a}\)），或者说，无论商品1和2的数量是多少，在消费者心中，1个商品1和\(\frac{b}{a}\)个商品2是一回事儿，我们称这两种商品为完全替代品。完全替代品不满足严格凸性的假设。

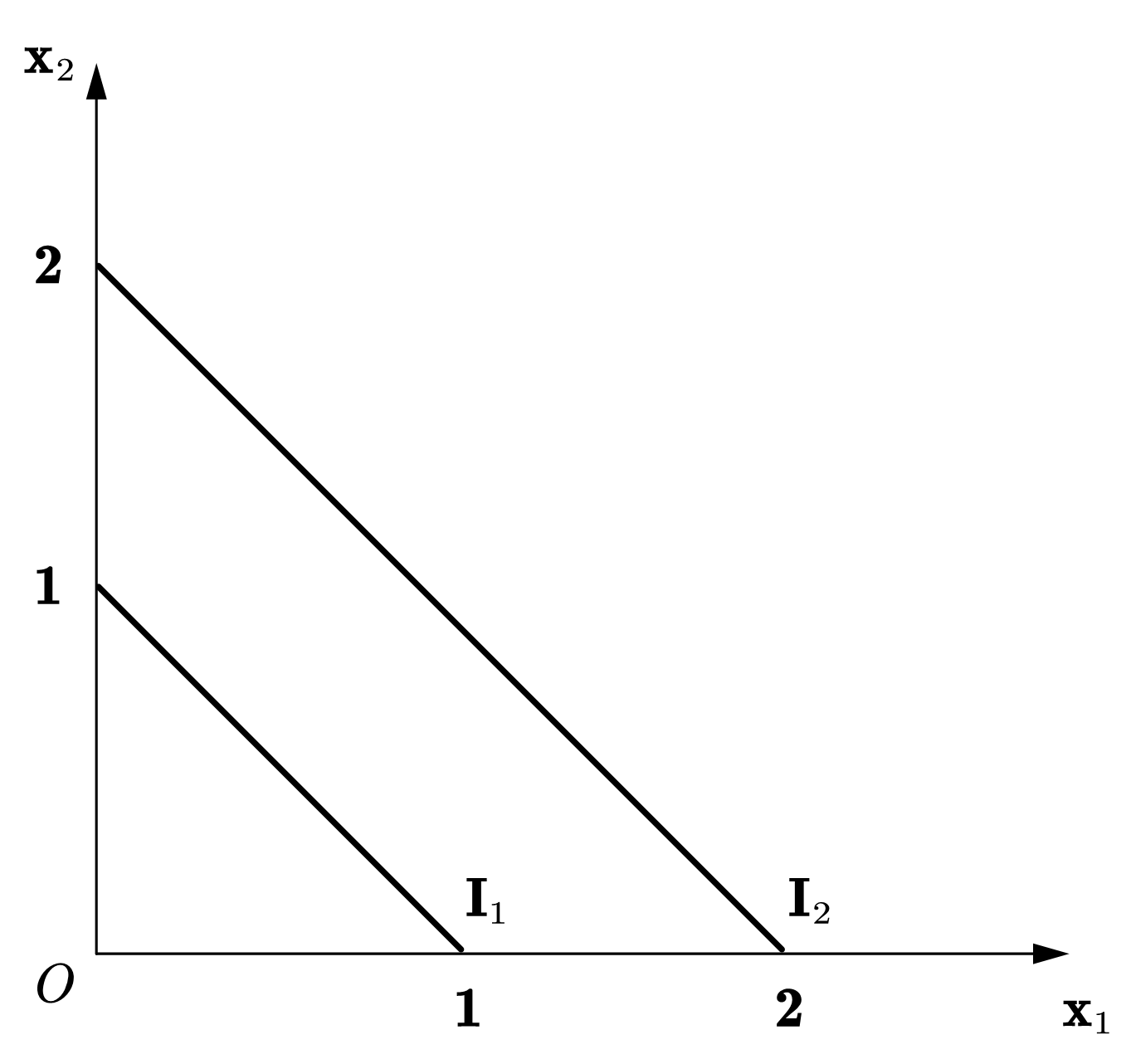
这表明商品1与商品2的无差异曲线为一条直线，斜率为\(-\frac{b}{a}\)（商品1在横轴），如图49(a)所示。我们可以将\(x_1\)与\(x_2\)的关系表示为：

\[ x_2 = -\frac{b}{a}x_1 + c \qquad (p.2) \]

其中，\(c\)为某条无差异曲线在纵轴的截距。由效用函数可以推出无差异曲线的表达式，相应的，由无差异曲线的表达式也可以推出效用函数，我们可以将上式调整为：

\[ ac = bx_1 + ax_2 \qquad (p.3) \]

不失一般性的，可以令\(U = ac\)，得到

\[ U = bx_1 + ax_2 \qquad (p.4) \]

\((p.4)\)即为一个描述完全替代品的效用函数。对\((p.4)\)做单调递增变换仍为表示同一个偏好的效用函数，比如

\[ U = \log (bx_1 + ax_2) \]

或者

\[ U = 20*(bx_1 + ax_2)^5-4 \]
(a) 完全替代品：1单位商品1等价于1单位商品2 (a) 完全替代品：1单位商品1等价于1单位商品2
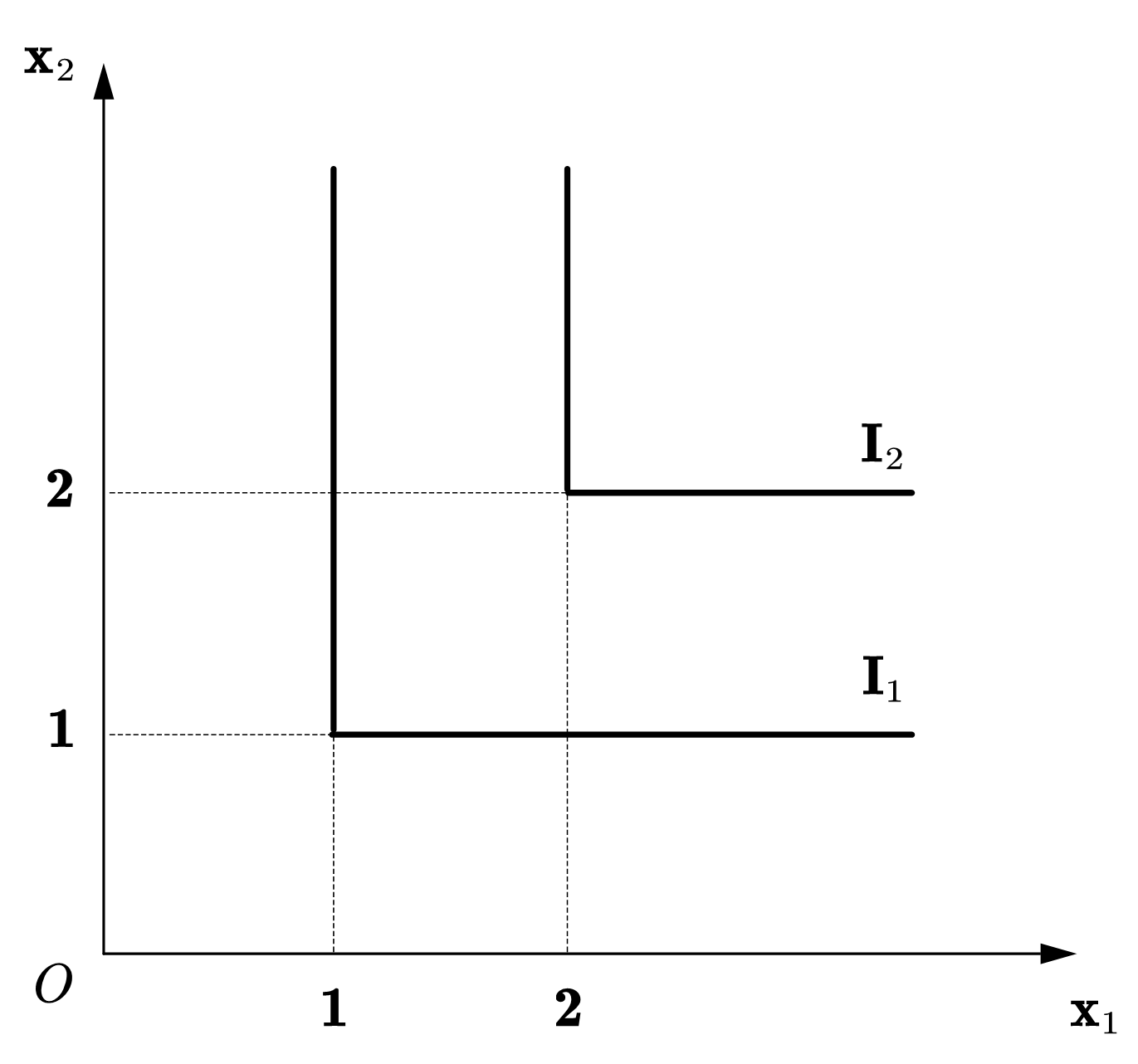
(b) 完全互补品：1单位商品1需要搭配1单位商品2 (b) 完全互补品：1单位商品1需要搭配1单位商品2

Fig. 49 两种特殊性状的无差异曲线#

完全互补品#

如果a个商品1必须搭配b个商品2共同消费——单方面增加某种商品的数量不会带来效用水平的变化，那么，我们称这两种商品为完全互补品。比如，一个眼镜架需要搭配2个眼镜片，眼镜架和眼镜片即为完全互补品。完全互补品不满足严格单调和严格凸性的假设。

完全互补品所对应的无差异曲线为向右侧开口的L型。如图49(b)所示，其中1单位商品1必须搭配1单位的商品2使用，无差异曲线中水平和垂直的部分表明如果单方面增加某种商品的数量，效用值不会发生改变。只有当两种商品按比例增加时，效用值才会增加。

什么函数可以用于描述商品数量单方面增加时，函数值不会改变的特征呢？

我们可以使用\(\min\)函数表示，不失一般性的，假设

\[ U = \min \{\alpha x_1, \beta x_2\} \]

\(\alpha\)和\(\beta\)为待决定的参数。\(\alpha x_1 = \beta x_2\)时，两种商品恰好满足搭配关系(\(x_1/x_2 = \beta/\alpha\))，若单独增加\(x_1\)或\(x_2\)，因为函数值由两部分的最小值决定，所以函数值不变，即效用值不变，符合完全互补品的特征。再由\(a\)种商品1必须搭配\(b\)种商品2，可得

\[ \frac{x_1}{x_2} = \frac{a}{b} = \frac{\beta}{\alpha} \]

令\(\alpha=b\)，\(\beta = a\)，得到效用函数

\[ U=\min\{bx_1,ax_2\} \]

相应的，对该效用函数做单调递增变换仍表示同一偏好，如

\[ U=(\min\{bx_1,ax_2\})^3 \]

预算约束#

预算约束是消费者实际上可以选择的消费束的集合，反映的是消费者客观的购买能力。显然，预算约束是消费集的子集，消费者负担不起的消费束，即使效用更高，也是无法得到的。

我们仍以两种商品进行分析，假设商品1和2的价格分别为\(p_1\)和\(p_2\)，消费者收入为\(I\)，预算约束可以表示为支出不高于收入的所有消费束的集合：

\[ \{\mathbf{(x_1,x_2)}|p_1x_2 + p_2x_2 \leq I\}\subset X \]

这里有一个暗含的假设：没有借贷市场，收入只能用于消费，这种设定简化了分析。或者也可以理解为消费者只进行一期的选择。我们之后可以放松假设，引入借贷市场，分析消费者跨期选择问题，其分析思路，最优条件和这里都是一致的。

n种商品的预算线可以表示为：\(\sum_{i=1}^n P_nx_n=I\)。

如图50所示，预算约束对应的是线段AB及其左侧区域。线段AB是支出恰好等于收入的消费束的连线，称之为预算线（也可称为消费可能线或价格线），满足\(p_1x_2 + p_2x_2 = I\)。预算线的横截距（纵截距）代表将收入全部用于购买商品1（商品2）的数量，即\(\frac{I}{p_1}\)（\(\frac{I}{p_2}\)），预算线的斜率为\(-\frac{p_1}{p_2}\)，代表的是用商品2表示的商品1的相对价格，即1单位的商品1在市场上相当于几单位的商品2，也可理解为两商品的经济替代率。

../../_images/ct-1-budget-line.png

Fig. 50 预算约束#

预算线将消费集分为了三个部分：

  • 预算线右侧是消费者负担不起的消费束（支出>收入）的集合。

  • 预算线左侧对应的是可负担同时收入所余的消费束（支出<收入）的集合

  • 预算线上的点表示恰好可以负担的消费束（支出=收入）

预算线#

在给定消费者收入和商品价格的条件下，消费者的全部收入所能购买到的消费束的集合。可以称为预算约束线、消费可能线或价格线。

下面我们思考一下当价格或/和收入变化时，预算线会如何变化。

  • 情境1： 收入变化。

    • 当收入增加时，\(\frac{I}{p_1}\)和\(\frac{I}{p_2}\)会增加，即横轴与纵轴的截距增加，且价格不变预算线的斜率不变，所以预算线会向外（右侧）平行移动。

    • 同理，当收入减少时，预算线会向内（左侧）平行移动。

  • 情境2：一种商品的价格发生变化。

    • 假设商品1的价格增加，首先，预算线斜率的绝对值，\(\frac{p_1}{p_2}\)，增加，横截距减少，而纵截距不变，所以，预算线会以纵轴交点为轴向内（左侧）旋转。换言之，商品1价格的增加，提高了商品1的相对价格，预算线斜率的绝对值增加，而纵截距不变，所以预算线会向内（左侧）旋转。

    • 同理，当商品1的价格减少时，预算线会以纵轴交点为轴向外（右侧）旋转。

    • 若商品2的价格变化呢？商品2价格增加，预算线会以横轴交点为轴向内（左侧）旋转；价格降低，会向外（右侧）旋转。

  • 情境3：两种商品的价格发生变化。

    • 若两种商品的价格同比例变化，这等价于收入变化。因为同比例变化不会影响商品的交换比率，所以预算线的斜率不变。价格同比例上升，相当于收入下降；价格同比例降低，相当于收入的上升。

    • 若两种商品价格变化的比例不同，则预算线的斜率和截距都会改变。

  • 收入和两种商品的价格同比例变化，预算线无变化。假设商品的价格和收入都为之前的\(\lambda\)倍（\(\lambda>0\)）

\[\begin{split} \begin{array} & (\lambda p_1)x_2 + (\lambda p_2)x_2 = \lambda I \\ \Leftrightarrow & p_1x_2 + p_2x_2 = I \end{array} \end{split}\]

附录#

(mrs-mu)==

证明：边际替代率递减不能推出边际效用递减规律#

假设效用函数为： \(U = u(x_1, x_2)\)

一些符号标记：

  • \(u_1 \equiv MU_1\)

  • \(u_2 \equiv MU_2\)

  • \(u_{11} \equiv \frac{\partial MU_1}{\partial x_1}\)

  • \(u_{12} \equiv \frac{\partial MU_1}{\partial x_2}\)

首先，计算\(\frac{d MRS_{12}}{dx_1}\)的表达式。注意消费束是在同一条无差异曲线上移动，当商品1的数量变化时，商品2的数量也会发生变化。

\[\begin{split} \begin{align} \frac{d MRS_{12}}{dx_1} & = & \frac{d(u_1/u_2)}{dx_1} \quad MRS_{12} =\frac{u1}{u2} \\ & = &\frac{\frac{d u_1}{d x_1}*u_2 - u_1*\frac{du_2}{dx_1}}{u_2^2} \quad (p.5) \\ & = & \frac{u_{11}u_2^2 - 2u_1u_2u_{12}+u_1^2u_{22}}{u_2^3} \quad (p.6) \end{align} \end{split}\]

我们可以基于下式由(p.5)推出(p.6)

  • \(\frac{du_1}{dx_1}=u_{11} + u_{12}\frac{dx_2}{dx_1}\)

  • \(\frac{du_2}{dx_1}=u_{21} + u_{22}\frac{dx_2}{dx_1}\)

  • \(\frac{dx_2}{dx_1}=-\frac{u_1}{u_2}\)

由边际替代率递减规律可得(p.6)为负值，即

\[ u_{11}u_2^2 - 2u_1u_2u_{12}+u_1^2u_{22}<0 \quad (p.7) \]

上式表明效用函数是严格拟凹函数。因为我们不能确定\(u_{12}\)的符号，所以不能确定\(u_{11}\)和\(u_{22}\)的符号，即无法推出\(u_{11}<0\), \(u_{22}<0\)。

同理，如果边际效用递减规律成立，基于(p.6)，我们也不能由\(u_{11}<0\), \(u_{22}<0\)推出(p.7)，即边际替代率递减。如果已知\(u_{12}=0\)，那么由\(u_{11}<0\), \(u_{22}<0\)可以推出(p.7)。