生产

生产#

我们将首先学习如何以抽象的方式描述企业的生产过程。技术这一概念被引入，用于描述投入转化为产出的过程。企业可以通过不同的投入组合来实现特定水平的产出。当只有一种产出时，我们可以使用生产函数的形式来表示企业的技术。我们将详细介绍生产函数的约束条件和特性。

其次，我们将在几何图中说明在其他要素投入固定不变的情况下，当只改变一种要素投入时，企业的产量会如何变化，并分析可能的要素投入范围。当企业可以改变至少两种要素投入时，我们将探讨在给定产量下，企业如何选择使成本最小化的要素投入组合。

值得注意的是，在本部分中，许多概念与消费者理论相对应，并可视为对消费者理论相关概念的检验。

学习目标

学完本部分，我们能够回答如下问题：

什么是技术？描述技术的方法？
什么是生产函数？
等产量线有哪些特征？
边际产量递减规和边际技术替代率递减规律的含义？
长期与短期的区别，以及如何理解？
规模报酬的含义和判断方法？
给定产量或成本下，企业最优要素投入所需满足的条件？
如何画出短期生产的相关曲线，各曲线的约束条件是什么？

技术——对生产的约束#

我们将生产定义为投入转化为产出的过程(Process of transforming inputs into outputs)。其中，

投入是指生产要素，包括劳动力，资本，原材料和土地等。资本可以包括物质资本和金融资本（货币形态的投入）。

对于生产要素，我们可以简单划分为劳动力（Labor）和资本（Capital）。对于劳动力和资本，我们还可以做进一步划分，比如劳动力可以划分为技术工人（skilled workers）、非技术工人（unskilled workers）和管理者等等；资本可以分为物质资本（非货币形态的）和金融资本（货币形态的），物质资本包括土地、机器设备、存货、厂房等等。有的书上将生产要素划分为劳动力、资本和原材料，或者将土地单独列出，划分为劳动力、资本和土地。在此，我们可以将资本做一般化的理解，即包含除了在生产函数中出现的其它和生产相关的要素。

产出是指生产的商品或服务，可以用于消费或进一步生产。
生产者是能够作出生产决策的单个经济单位，包括个人、合伙和公司性质的组织形式。企业是其中的重要组成部分。

我们可以将生产的过程视为一个“黑匣子”，只需要关注「输入」与「输出」，而不用考虑中间的具体生产程序、方法和操作等。

技术（Technology）是对生产的约束，决定了投入与产出的所有可能——告诉我们对于给定的要素投入，有哪些可能的产量；或者，对于既定的产量，有哪些可行的要素投入组合。除了生产技术外，生产方式、管理、合约结构和法律约束等等也是影响技术的因素，比如，在同样的要素投入下，不同的机器排列顺序可能会对产量产生影响。在《丰田生产方式》中，大野耐一指出将流水线机器的排列方式由“二”字型或“L”字型，改为“口”字型和“］”字型后，生产效率得到了提高（投入产出关系发生了变化）（[]）。再比如，不同的工资合约——如件工合约或小时合约——也会对劳动生产率产生影响。

技术可以用生产计划和生产集描述。生产计划（也可称为生产束）是投入与产出数量的集合，表示在给定技术下的一种生产可能，如 \(\mathbf{y}= (y_1,\dots,y_m)\) 。其中， \(y_i<0\)表示投入， \(y_i>0\)表示产出。生产束适用于描述多投入和多产出的情况，比如，\(\mathbf{y}=(-3,-2,1,2)\) 表示有两种生产要素和有两种产出，当要素投入数量分别为3单位和2单位时，产量分别为1单位和2单位。生产集(Production Possibility Set)，\(Y \subset R^m\)，是所有可行的生产计划的集合，\(\mathbf{y} \in Y\)。

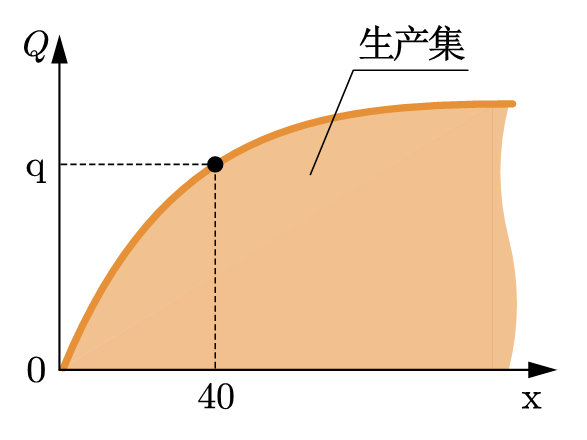
图64描述的是生产集，集合中的每个点表示一个可行的生产计划（在图中，我们将要素投入调整为了正值）。生产集的边界——图(a)中的边界线或图(b)中的边界曲面——代表的是给定要素投入下的最大产量，被称为「技术上有效率的生产计划」（technically efficient production plan）。例如，在图(a)中，40单位的要素投入最多可生产q单位的商品。

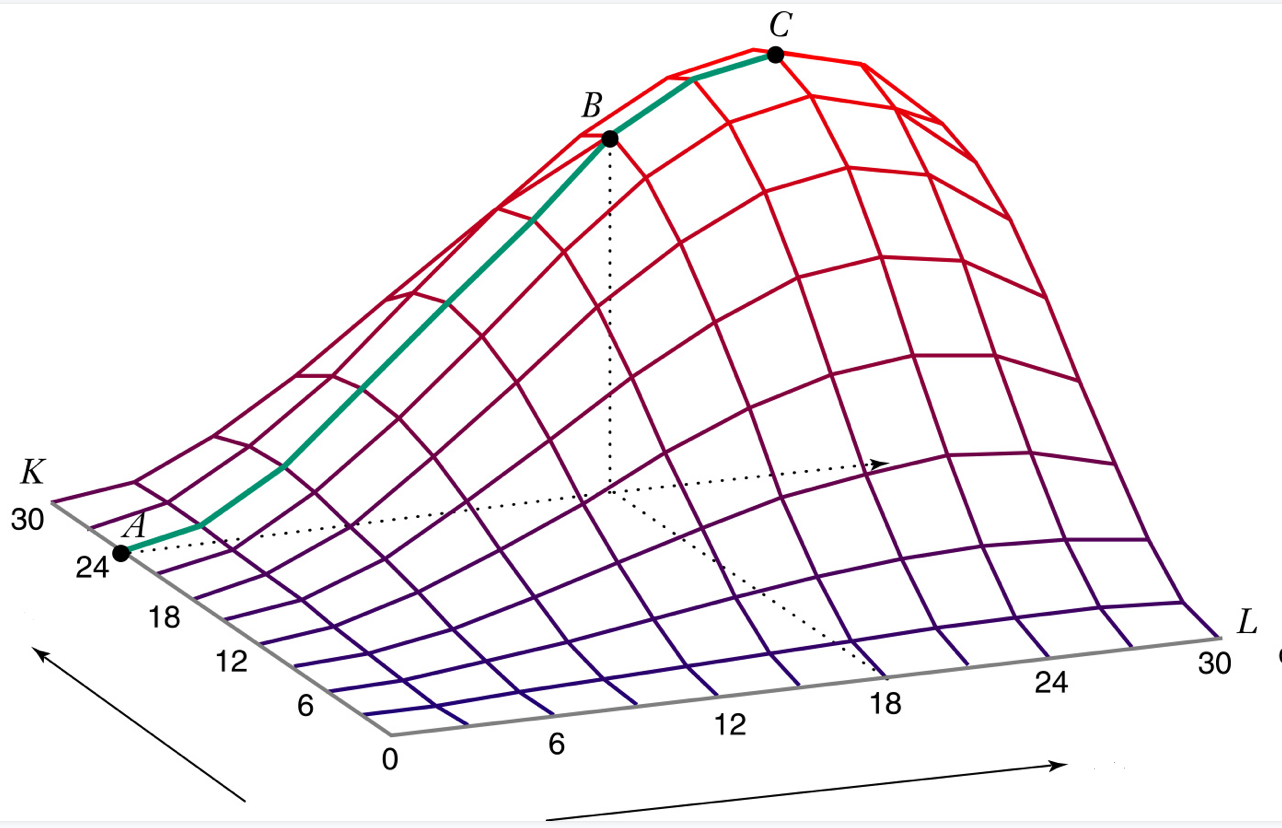
当生产要素的数量不止是一种时，对于同样的产量，可以对应多种技术上有效率的要素组合的方式，如图64(b)所示，对于同样的最大产量，企业可以多使用劳动力少使用资本（劳动密集型）或多使用资本少使用劳动力（资本密集型）。这说明企业的投入具有灵活性的，比如，企业可以通过技术替代应对员工成本的上升。

在接下来的分析中，我们都假设企业只有一种产出，或者说，企业使用的是一种产出的生产技术（one-output technology）。当只有一种产出时，我们可以用函数描述投入与产出的关系，称为生产函数。

生产函数#

因为企业的生产目标是最大化利润，所以企业一定会使用技术上有效率的生产计划安排生产，否则便会存在投入上的浪费。因此，我们将生产函数，\(f: R_+^n \rightarrow R_+\)，定义为在一定时期内，给定技术水平，生产中使用的各种投入数量与产出的最大数量之间的关系（技术上有效率的生产关系），如

\[ Q = f(\mathbf{x})=f(x_1,x_2,\dots,x_n) \]

其中，\(\mathbf{x}=(x_1,x_2,\dots,x_n)\)代表要素投入数量的集合，比如，\(\mathbf{x}=(1,3,5)\)的含义是有三种要素，投入数量分别为1，3和5单位; \(Q\)代表产量；\(f\)代表生产集边界的技术约束。

需要注意的是，首先，现实中的生产通常会存在产能限制，因此投入是有限的，不能无限增加。其次，生产函数存在时间维度，产量与要素投入均为流量(flow variable)。将劳动力和原材料视作流量较为直观，而长期使用的资本，比如数控机床，似乎作为存量理解更为恰当。为了避免理解上的矛盾，我们可以将资本的数量理解为其在生命周期内的一段使用时间，比如使用每年使用的小时数来表示资本的投入。如果未特别提及，我们默认生产函数代表一年内的投入和产出关系。

接下来，我们需要给生产函数加上一些假设条件，这些条件是对技术的约束。

生产函数的假设#

假设1：连续性。

假设2：严格递增。只要有一种要素投入增加，产量便会增加，即

\[ \mathbf{x'} \geq \mathbf{x} \quad \& \quad \mathbf{x'} \neq \mathbf{x} \quad \Rightarrow \quad f(\mathbf{x'})>f(\mathbf{x} ) \]

在此，我们需要将投入限制在企业的产能约束之内，并且企业不会在边际产量为负的情况下进行生产，因此我们无需考虑这种情况。鉴于此，对于任何一种要素组合，我们都假设要素的边际产量为正，即，当至少有一种要素的数量增加时，产量也会增加。

假设3：严格拟凹。对于产量为\(q\)的要素投入集合\(\mathbf{x}^1\)和\(\mathbf{x}^2\), 对于任意\(t\in[0,1]\)，可得

\[ f(tx^1 + (1-t)x^0) > q \]

与严格拟凹假设等价的是技术具有严格凸性。这个假设表明生产要素会具有一些互补性，和「不均衡的」的投入组合相比，「均衡」的投入组合会带来更高的产出。(Production needs a balanced mix of both inputs)

假设4：企业是可以停产的，即\(f(\mathbf{0})=0\)。

这也说明企业不能无中生有——有产出必有投入。

边际产量和边际技术替代率#

边际产量（Marginal Products）代表的是要素投入的边际变化（增加1单位）对总产量的影响。计算某种要素的边际产量时，需要确保其它要素的投入量保持不变。如果生产函数是可微的，我们可以用导数表示要素 \(i\) 的边际产量：

\[ MP_i = \frac{\partial f(\mathbf{x})}{\partial x_i} \quad \forall i \]

严格递增假设含义着边际产量为正（\(MP_i>0\quad \forall i\)）。

边际技术替代率（Marginal Rate of Technological Substitution，MRTS）描述的是在产量不变的前提下，两种生产要素的替代关系，也可以称为技术替代率（Technical Rate of Substitution, TRS）。要素\(i\)对要素\(j\)的边际技术替代率（\(MRTS_{ij}\)）含义着，在给定要素投入组合处，如果增加1单位要素\(i\)需要减少几单位的要素\(j\) 以保持产出不变。同样，如果生产函数可微，我们也可以使用导数表示：

\[ MRTS_{ij} = -lim_{\Delta x_i \rightarrow 0}\frac{\Delta x_j}{\Delta x_i}|_{\bar{Q},\ \mathbf{x}} = -\frac{\partial x_j }{\partial x_i}|_{\bar{Q},\ \mathbf{x}} \]

其中，\(\bar{Q}\)为给定的产量。由于边际技术替代率被定义为正值，而且基于严格递增假设，为了保持产量不变，两要素需在一增一减的方向上进行变化。因此，在上式中需要加入负号。

假设有两种要素投入，通过对生产函数做全微分，可以推出边际产量与边际技术替代率的关系：

\[ MRTS_{12} = \frac{MP_1}{MP_2} \]

证明：\(MRTS_{12} = \frac{MP_1}{MP_2}\)

\[\begin{split} \begin{align*} & f(x_1,x_2) = \bar{Q} \quad \text{计算MRTS需要满足产量为定值}\\ \Rightarrow & \frac{ \partial f(x_1,x_2)}{\partial x_1}dx_1 + \frac{ \partial f(x_1,x_2)}{\partial x_2}dx_2 = 0\\ \Rightarrow & -\frac{dx_2}{dx_1} = \frac{MP_1}{MP_2}\\ \Rightarrow & MRTS_{12} = \frac{MP_1}{MP_2} \end{align*} \end{split}\]

相似的，如果有多种要素投入，我们可以定义两要素的边际技术替代率等于它们的边际产量之比：

\[ MRTS_{ij} = \frac{MP_i}{MP_j} \quad \forall i,j = 1,2, \dots, n \]

等产量线#

在现实中，企业的生产会涉及各种生产要素及其不同的组合。为了简化分析，我们可以将生产函数简化为只有两种要素投入——劳动力和资本，以便分析企业的产出决策，

\[ Q = f (L,K) \]

其中，\(L\)代表劳动力的投入数量（使用每年工作的小时数进行衡量）；\(K\)代表资本的投入数量。

与消费者理论的分析思路一致，之所以选择两种要素进行分析，一是因为便于几何分析；二是基于两种要素投入的最优条件，我们很容易地扩展到更多的生产要素上去。

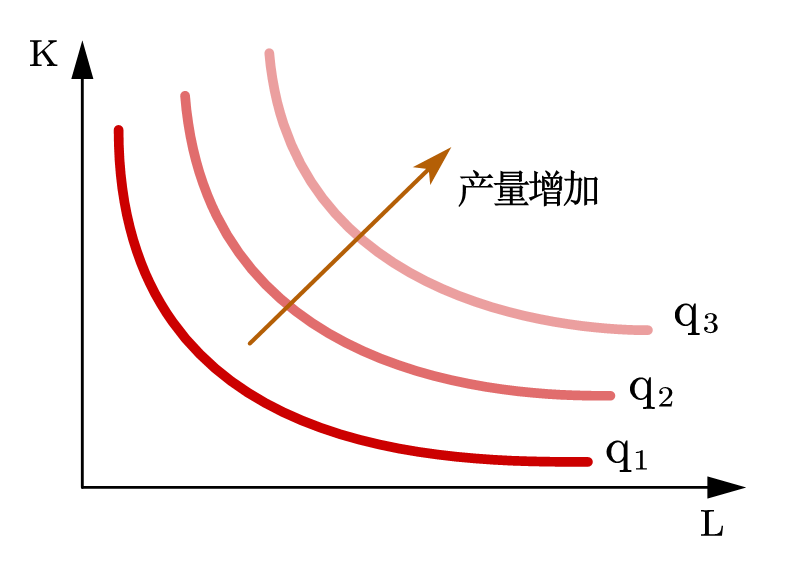
在两要素数量的坐标系内，将具有相同最大产量的要素组合相连，所构成的曲线被称为等产量线。显然，等产量线和无差异曲线是相对应的概念。不同之处在于，产量具有实际意义并且是基数的，而效用是序数的，没有实际意义，同一个偏好可以对应不同的效用函数。

习惯上，我们会把劳动力（或要素1）的数量放在横轴，资本（或要素2）的数量放在纵轴，如图65 (a)所示。等产量线对应的是生产集的边界曲面的等高线，其上的要素投入组合都是技术上有效率的。等产量线的集合是对生产函数的几何描述。

基于生产函数，我们可以推出等产量线的表达式：

\[ \bar{Q}=f(K,L) \Rightarrow K = f^{-1}(\bar{Q},L) \]

\(\bar{Q}\)为某条等产量线所对应的产量。

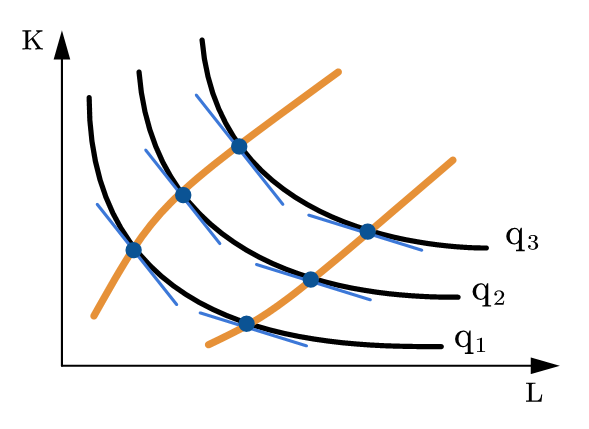
等产量线切线斜率的绝对值等于在给定要素组合下的劳动力对资本的边际技术替代率。将具有相同边际技术替代率的要素组合相连，所构成的曲线称为「等斜线」。如图65 (b)所示，给定一个边际技术替代率的取值，就可以画出一条等斜线：

\[ \{(L,K)|MRTS_{L,K} = m, m\in R^{+}\} \]

很显然，在同一条等斜线上，过每一点所画出的在其对应等产量线上的切线是平行的。

等产量线的特征#

特征1：等产量线向右下方倾斜，斜率为负。

特征2：等产量线不相交。

特征3：离原点越远的等产量线代表的产出越高。
特征4：等产量线凸向原点。

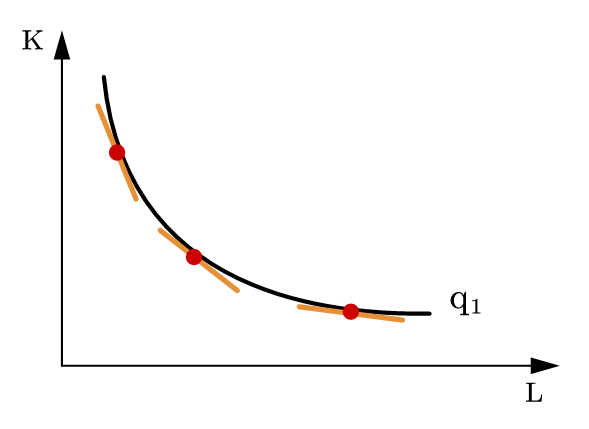
该特征源于严格拟凹假设：对于在同一等产量线上的两个要素投入集合，在它们连线上的要素组合（凸组合）会带来更高的产量，如图66。

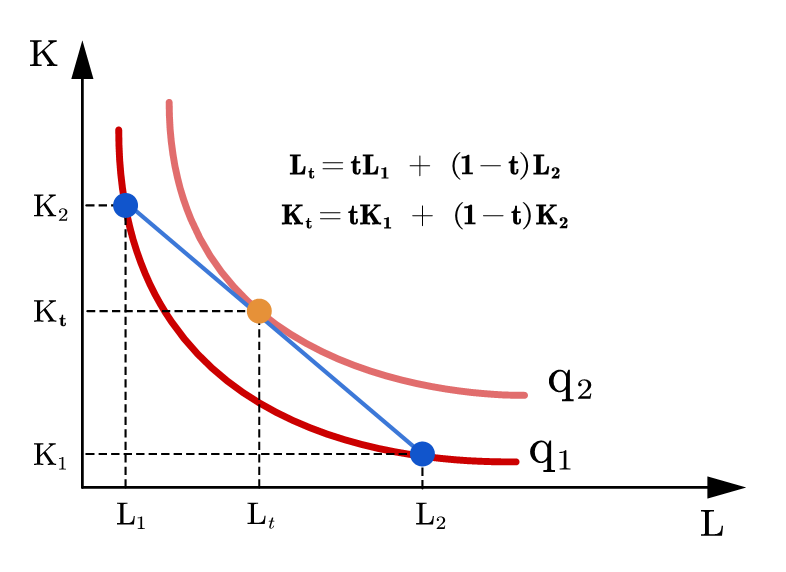
../../_images/L4-production-conves-property.png — Fig. 66 等产量线凸向原点#

边际技术替代率和边际产量递减规律#

如图67 (a)所示，等产量线凸向原点含义着劳动力对资本的边际技术替代率随着劳动力的增加而递减，换言之，随着劳动力的增加，企业为保持产量不变所减少的资本投入越来越少，我们将此特征称为边际技术替代率递减规律：

\[ \frac{dMRTS_{LK}}{dL}<0 \]

(a) 边际技术替代率递减 — Fig. 67 边际技术替代率和边际产量递减规律#

(b) 劳动力的边际产量递减 — Fig. 67 边际技术替代率和边际产量递减规律#

边际产量递减规律是指当企业不断的增加某种要素的投入量时，边际产量最终一定是递减的。具体而言：在一定技术水平下，其它要素投入不变时，企业连续等量地增加某一种生产要素，当这种生产要素的投入量超过某一数量时，增加该要素投入所带来的边际产量是递减的。在代数上，边际产量递减规律表现为生产函数对相应要素的二阶偏导小于0：

\[ \frac{\partial MP_L}{\partial L} <0 \quad \frac{\partial MP_K}{\partial K} <0 \]

虽然从理论上讲，可能出现不断增加投入量导致边际产量为负的情况，但从效率角度看，企业不会在产出为负时进行生产，因此这与严格递增假设并不冲突。

在《巴菲特给股东的信》一书中有这样一句话：“以我们今天运作的这样的庞大资本，很难达到在资本规模小的多的时候所取得成就。我们对内在价值增长率的最高期望是平均每年15%，而我们可能与这个目标相距甚远”。这恰是边际产量递减规律的体现。事实上，资本规模越大，投资的难度就越大，相应的回报也会降低。再如一句俗语所言：“两个和尚挑水，三个和尚就没水喝”，这也体现了边际产量递减规律。

边际产量递减规律的几何描述如图67 (b)所示，假设资本数量保持不变，随着劳动力数量的等量增加，产量增加量是下降的。如，劳动力从5单位增加到6单位时，产量的增加量为20单位；而从6单位增加到7单位时，产量的增加量为15单位。或者从另一个角度看，对于产量等量增加的等产量线来说，它们之间的距离会逐渐增大。

在计算边际产量时，我们需要保持其它要素投入不变，这个前提使边际产量具有代数上表示的便利性。但是，在现实应用中，边际产量递减规律却不一定需要满足「其它要素投入不变」这个前提，我们思考以下两个情景：

情境1：当生产要素的数量多于两种时，只要有一种要素之量保持不变，其它要素的增加迟早会带来边际产量的下降。考虑在一定面积的厂房内，不断增加劳动力，原材料，机器，当出现挤迫后，各种要素相互干扰，边际产量会出现下降。再以花盆种菜为例，花盆的大小不变，我们不断地往里面加土、施肥和浇水，最终也会出现边际产量递减。
情境2：假设所用要素都增加，但是增加的比例不同，比如劳动力增加的速度快于机器设备增加的速度，假设两者之比的变化为：5/1, 12/2, 20/3, 40/4 … ，那么，增加速度较快的生产要素最终也会出现边际产量下降。

或者，仍以花盆里种菜为例，如果花盆也在扩大，土、肥料和水也在不断增加，但是水的增速是最快的，最终，菜苗可能会涝死，这也是边际产量递减的提现。

因此，只要有一种要素固定不变，或要素的变动比率有所不同，边际产量下降迟早也时会出现的。这说明，在现实中应用边际产量递减规律时，我们可以放松其前提假设条件——其它要素投入量保持不变。

边际产量递减规律类似于边际效用递减规律，但是两者之间有重要区别。边际产量递减规律是一种经济现象，原则上可以被检验；而边际效用递减规律则是一种心理现象，无法被验证。

虽然边际产量在现实中不易度量，使检验这一规律变得困难，但是我们可以从反方向加以思考。如果没有边际产量递减规律，那么我们理论上就能够在有限的花盆中种植出足够全世界所需的粮食，然而这是不现实的。

边际产量递减规律还意味着，如果技术水平不变，社会总产量不会无限增长。因此，经济增长最终来自技术的进步。技术进步可以突破边际产量最终下降的限制。如图68所示，技术进步会使生产集边界上移，即在给定投入下，最大产出增加。

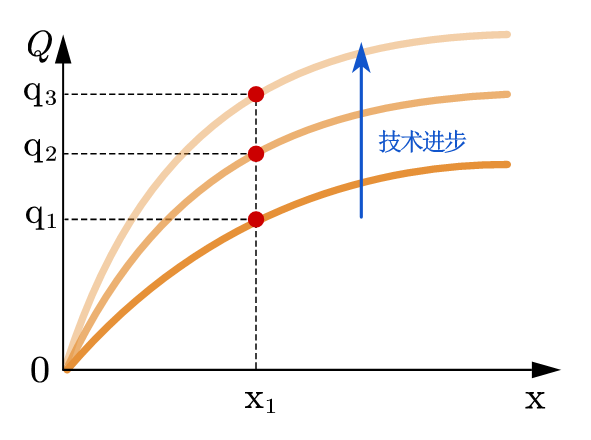
../../_images/L4-production-tech-improve.png — Fig. 68 在相同的投入下，技术进步会带来产量的增加。#

需要注意的是，边际产量递减规律是对生产函数的额外约束，并非源于生产函数的基本假设。与边际替代率和边际效用递减规律的关系一致，边际产量递减规律和边际技术替代率递减规律并不是相互推导的关系。边际技术替代率是定义在同一条等产量线上，而边际产量描述的是等产量线间的关系。边际产量递减时，等产量线可以凹向原点；等产量线凸向原点时，边际产量可以是递增的。

规模报酬（Return to Scale, RTS）#

规模报酬描述了生产要素同倍数变化与产量之间的关系。假设所有生产要素都变化相同的比例，\(\lambda\)（\(\lambda >1\)），我们可以通过比较\(f(\lambda L, \lambda K)\) 和\(\lambda f(L,K)\)，定义规模报酬的三种类型：

如果\(f(\lambda L, \lambda K) > \lambda f(L,K)\quad \forall L,K\)，即产量变化的倍数大于\(\lambda\)，则称此生产函数具有规模报酬递增（IRTS）的特征；
如果\(f(\lambda L, \lambda K) = \lambda f(L,K)\quad \forall L,K\)，即产量变化的倍数等于\(\lambda\)，则称此生产函数具有规模报酬不变（CRTS）的特征；
如果\(f(\lambda L, \lambda K) < \lambda f(L,K)\quad \forall L,K\)，即产量变化的倍数小于\(\lambda\)，则称此生产函数具有规模报酬递减（DRTS）的特征。

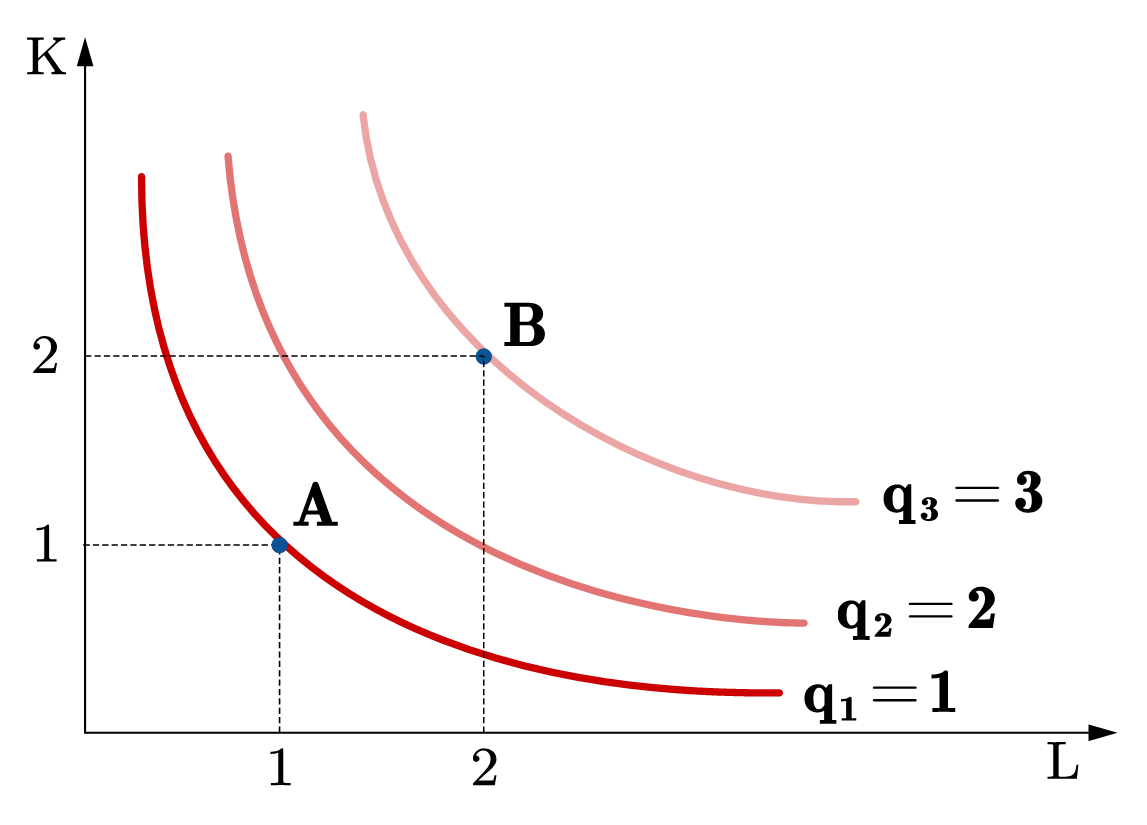
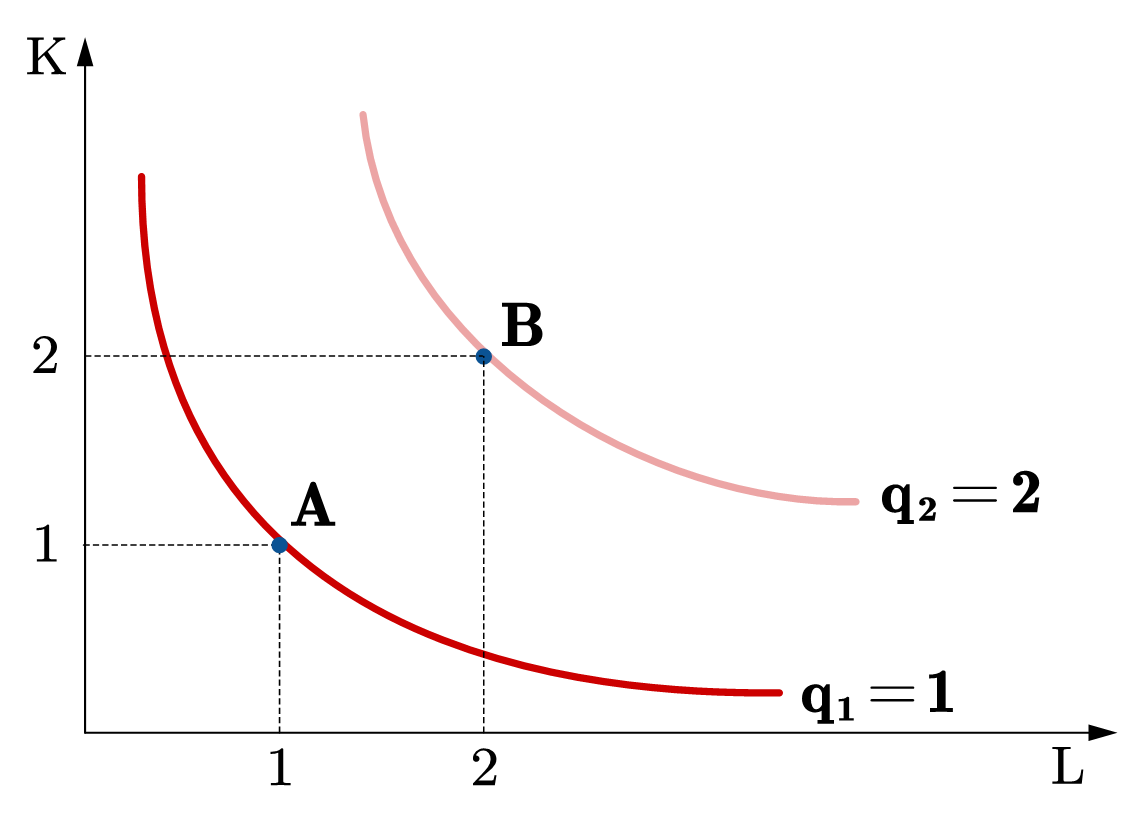
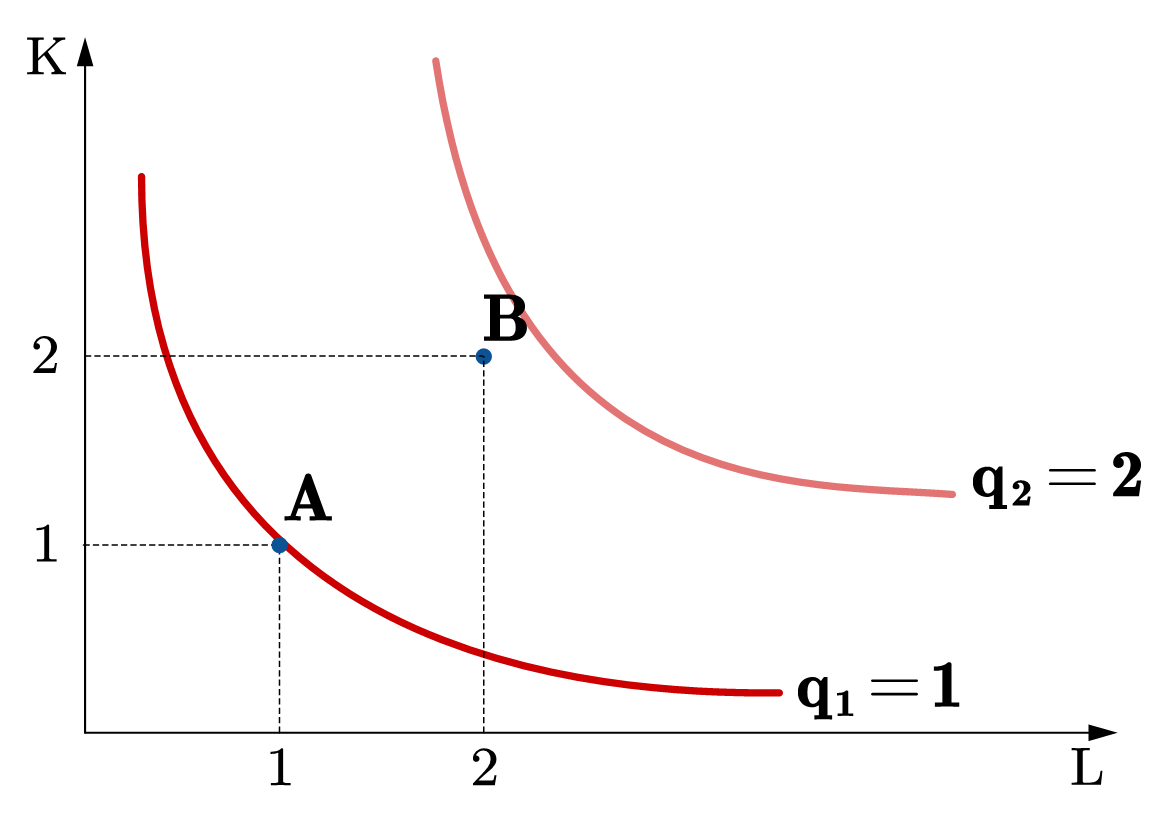
在图69中，在\(q=1\)的等产量线上，我们选定了一个要素投入组合，\((L,K)=(1,1)\)，表示为A点。假设所有要素投入增加了一倍，\((L,K) = (2,2)\)，表示为B点。在图(a)中，B点的产量等于3，是A点产量的3倍，对应的是规模报酬递增；图(b)的B点的产量等于2，恰好是A点产量的2倍，对应的规模报酬不变；图(c)中的B点的产量小于2（在\(q=2\)等产量线的左侧），对应的规模报酬递减的特征。

规模报酬定义的是生产函数的全局特征——所有的要素投入组合都需要满足对应的条件，这显然是很强的约束条件。随着要素投入的变化，生产函数的规模报酬特征是有可能发生变化的，如图70所示。因此，生产函数并不必然是规模报酬不变，递增或递减的。

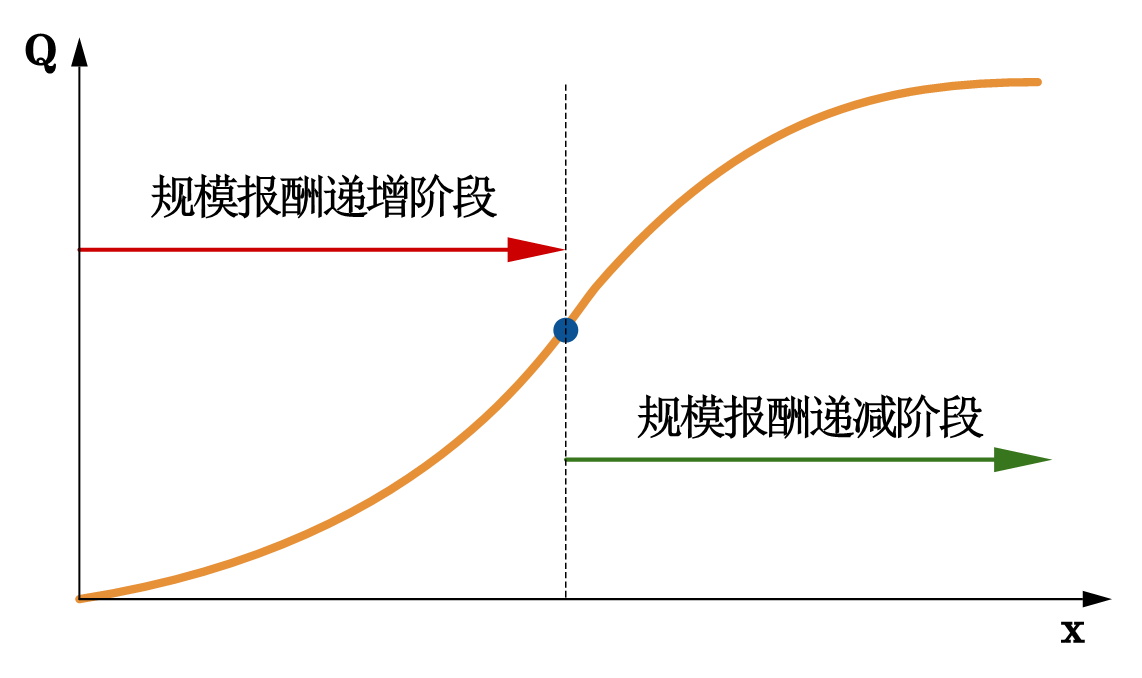
../../_images/L4-production-irts-drts.png — Fig. 70 总产量曲线：一种投入，一种产出。#

判断生产函数的规模报酬特征。

假设生产函数为：

\[ Q = L^{\alpha}K^{\beta} \]

判断这个生产函数的规模报酬特征，需要比较 \(f(λL, λK)\) 与 \(\lambda f(L,K)\)的关系，

\[ f(λL, λK)=(\lambda L)^\alpha (\lambda K)^\beta = \lambda^{\alpha+\beta}L^{\alpha}K^{\beta} \]

可以得到，

当\(\alpha+\beta>1\)时，\(\lambda^{\alpha +\beta}>\lambda\)，生产函数呈规模报酬递增的特征；
当\(\alpha+\beta = 1\)时，\(\lambda^{\alpha +\beta} = \lambda\)，呈规模报酬不变的特征；
当\(\alpha+\beta<1\)时，\(\lambda^{\alpha +\beta}<\lambda\)，呈规模报酬递减的特征。

长期与短期#

我们可以将企业的生产决策划分为长期决策和短期决策（planning decision）。长期和短期会影响生产函数的特征。

长期和短期的划分是以企业调整要素投入的灵活程度为衡量标准：长期是指所有要素投入量都可以灵活调整；短期是指有些要素投入量不能被调整。长期和短期并不是独立于企业生产过程的时间范畴，短期不一定比长期短，长期不一定比短期长。

我们将可调整的要素称为可变要素，而不能被调整的要素称为固定要素。对于固定要素，我们用带有上划线的变量表示，比如\(\bar{K}\)表示资本的数量为K且不会随产量变化而改变。在长期，所有生产要素都是可变要素，对应的生产函数被称为长期生产函数；而在短期，生产要素会被划分为可变和固定要素，对应的生产函数则被称为短期生产函数。

前面定义的边际产量递减规律是短期生产函数的特征，这是因为其前提条件是其它要素投入量不变，相当于是有些要素的数量是无法调整的。而规模报酬属于长期范畴，是长期生产函数的特征。

通常情况下，我们假设资本是固定要素，如\(Q = f(\bar{K},L)\)。显然，设备和厂房等要素是不易进行调整的。然而，在现实中，将资本视为固定要素并不是绝对的。比如，对于一些轻资产的企业，员工可以在家办公，资产主要是租用的云端服务器。如果这家企业劳动合同比较严格，这时劳动力反而可能相对难以调整，此时将资本视为固定要素就不合适了。需要注意的是，要素是固定还是可变是与合约结构有关的。如果企业与员工签订的是固定期限合约，那么劳动力就有可能具有固定要素的特征。

之所以将企业决策划分为长期和短期，是因为当生产要素都可以灵活调整时，企业可以从所有可行的生产计划中选择成本最低的生产方法来达到效率最大化。。而在短期，企业的选择受到固定要素的限制。由于这些要素无法灵活调整，企业的选择和决策会受到约束。因此，短期决策更多地依赖于新的市场信息和当前可用资源的权衡。

一些轻资产企业

Airbnb是一家在线民宿预订平台，它通过云端服务器搭建和管理平台。相对于传统酒店业务，Airbnb的资产投入较少，核心业务主要依赖于互联网平台和技术。虽然他们需要一些固定要素，如办公空间和服务器设备，但相比于实体酒店的资产投入，这些要素相对来说是比较灵活和容易调整的。

然而，与资产相比，Airbnb 最重要的资源是与房东和房客建立联系并提供服务的员工。这些员工在保持平台运转和提供良好用户体验方面发挥着关键作用。与资产相比，劳动力是不太容易调整的要素。

哔哩哔哩（Bilibili）是一家在线视频平台，主要以动画、游戏、影视等内容为主。哔哩哔哩的业务模式主要基于在线视频平台和用户社区，资产投入相对较少，而劳动力调整可能更多涉及到内容创作者、运营团队和技术团队等。

作为一个在线视频平台，哔哩哔哩的资产投入主要集中在技术基础设施、服务器和平台开发方面。相对于传统媒体公司而言，哔哩哔哩的资产投入较少，主要依靠云端和在线技术来支持平台的运营。这使得哔哩哔哩能够更加灵活地扩展和调整其平台规模和功能。

哔哩哔哩的核心竞争力来自于其内容创作者、运营团队和技术团队。内容创作者负责制作和上传各种原创动画、游戏视频和影视内容，而运营团队负责管理和优化平台的用户体验和社区氛围。技术团队则负责维护和发展平台的技术架构和功能。

对于长期和短期定义，我们可以从下面的对话中体会出一些套套逻辑的意味：

Q: 为什么企业有些要素是不能调整的呢？
A：因为处在短期。
Q: 那短期指的是什么呢？
A: 有些要素不能调整。

我们应如何理解短期和长期的概念呢？长期可以被视为企业进入市场之前的决策阶段。在这个阶段，企业的所有安排都在计划中，还没有在现实中执行，因此所有要素的调整都是可能的。企业可以根据需求扩大厂房设计以增加产能，调整劳动力的雇佣计划，改变产品的工艺设计或调整生产流程等。然而，一旦企业投资进入市场，如购买房产、建造厂房、安装设备或雇佣员工等，一些要素的调整将受到限制。比如，已经建成的厂房难以扩张，合约期内的员工难以解雇。在这种情况下，企业只能在长期决策的基础上，结合新的市场信息进行受限制的决策。因此，这些决策被归类为短期范畴。

长期决策：企业进入市场之前的决策

短期决策：企业进入市场之后的决策

最后，我们再来思考一个问题：对于在短期的固定要素，这个固定不变是真的不能改变吗？

以炼钢厂的炼钢炉为例，它通常被视为一个固定要素，因为它不能轻易停工。但是，为什么不能停工呢？从逻辑上来看，我们可以通过拉闸断电来停止运行。所以，不停工并不是简单地不可改变的结果，而是基于权衡和选择。

实际上，炼钢炉随意停运可能会导致一系列问题。炉内温度会下降，未排出的熔化铁水会推满炉膛底部。再次启动炉子需要消耗大量电力，并且设备也可能因停运而报废，以及重新点火需要预热阶段等等。这些都会产生巨大的成本，可能高达上百万甚至上千万。因此，除非是炉子发生故障或被迫停工，企业不会轻易停运炼钢炉。

综上，固定要素非完全不可改变，调整与否往往涉及到一系列成本和效益的权衡。正因为是选择不变，我们才能够去分析持有固定要素的机会成本。

三种形式的生产函数#

科布道格拉斯生产函数（Cobb-Douglas Production Function）#

在消费者理论中，我们已经熟悉了科布-道格拉斯形式的效用函数。这种函数形式也可以用于表示生产函数，比如：

\[ Q = K^\alpha L^\beta \]

通常我们会假设\(\alpha+\beta=1\)。

布道格拉斯函数的由来

科布道格拉斯函数的命名源于两位学者：数学家科布和经济学家道格拉斯。

道格拉斯在研究美国的投入产出数据时，发现劳动力和资本这两个要素在每一年回报的占比基本恒定。于是，他去咨询了数学家柯布，是否可以使用一个生产函数描述这个现象。后人便把科布所使用的函数形式称为科布-道尔斯生产函数。

所以，科布-道尔斯生产函数的构造特征便是要素回报的占比是定值，这也是为什么科布-道尔斯效用函数具有商品最优选择支出占比是定值的特征。

check 下面我们简单说明一下为什么科布道格拉斯生产函数的要素的收入占比恒定。

首先，在最优投入处，要素的单位价格等于其边际产量，在这里我们用商品去衡量价格。比如，资本的单位价格为\(MP_K\)，劳动力的单价为\(MP_L\)。基于科布道格拉斯生产函数，可得：

\[\begin{split} MP_K = \alpha K^{\alpha-1}L^{\beta}\\ MP_L = \beta K^{\alpha}L^{\beta-1} \end{split}\]

生产函数为（\(\alpha + \beta\)）阶齐次函数，由欧拉定理可得，

\[ K*MP_K + L*MP_L = (\alpha+\beta)Q \]

表明资本和劳动力的总回报为\((\alpha+\beta)Q\)，可以计算两要素的回报占比为定值：

\[\begin{split} \frac{K*MP_K}{(\alpha+\beta)Q} = \frac{\alpha}{\alpha+\beta}\\ \frac{K*MP_L}{(\alpha+\beta)Q} = \frac{\beta}{\alpha+\beta} \end{split}\]

固定替代比例生产函数#

固定替代比例是指生产要素在生产上是完全替代的，它们的边际技术替代率为定值，生产函数的基本形式为线性函数，如：

\[ Q=aL+bK \]

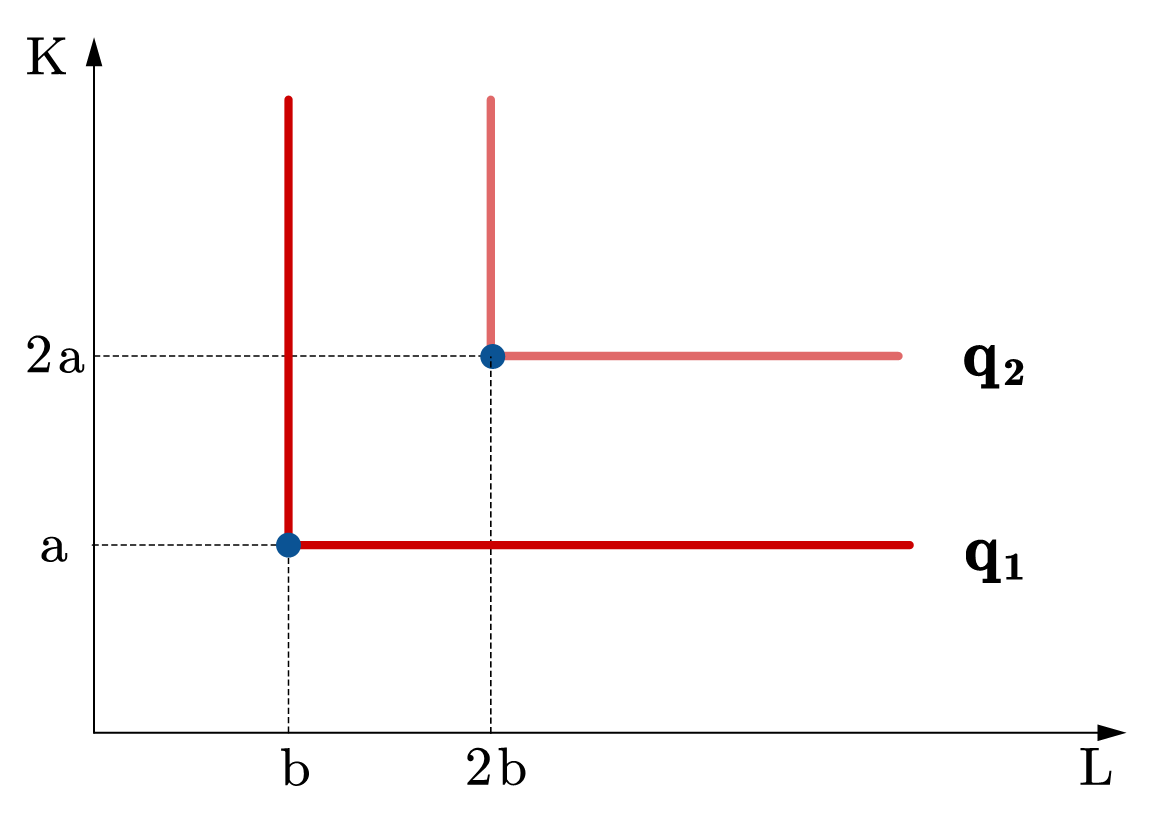
其中，\(a\)，\(b>0\)是参数，b单位劳动力与a单位资本的产出相同，皆为ab单位，且\(MRTS_{LK}=a/b\)，对应的等产量线是一条直线，如图71 (a)所示。很显然，线性生产函数是特殊性状的生产函数，不满足严格拟凹假设。

固定投入比例的生产函数#

固定投入比例的生产函数也可以称里昂锡夫（Leotief）生产函数。固定投入比例是指要素投入比例需要满足既定的比例，单独增加要素投入不会带来产量的增加，其生产函数的基本形式为：

\[ Q = \min \{aL,bK\} \]

其中，\(a\)，\(b>0\)是参数，劳动力与资本的投入之比应满足\(b:a\)。等产量线如图图71 (b)所示，是向右侧开口的L型。里昂锡夫生产函数也是特殊性状的生产函数，不满足严格递增和严格拟凹假设。

生产决策——如何决定最优投入#

在学习了如何描述生产之后，接下来，我们希望分析企业的最优要素投入。为了简化分析，我们假设生产要素的价格是外生给定的，这使得我们可以将要素投入的考虑与商品的供给问题分开。

由于要素投入通常具有一定的替代性，不同的投入组合可能会带来相同的最大产出。在给定要素价格的情况下，这些要素组合的成本是不同的。技术上有效率的投入组合不一定是经济上有效率（成本最低）的。因此，这引出了所有企业面临的基本问题：如何以最低的成本选择要素投入来生产给定的产出？在这里，我们的分析目标是找到企业最优生产决策的条件。

让我们再明确一下「最佳决策」的含义。因为对于给定的产出，可能存在多个技术上有效率的要素投入组合。因此，从企业的经济目标出发，我们需要选择经济上最有效（成本最低）的选择。

需要注意的是，最优要素投入选择的分析适用于有两种或更多可变要素（包括长期和短期）的投入决策。如果只有一种可变要素，我们可以通过产量直接求解要素投入。

只有一种可变生产要素（劳动力）#

假设在生产函数为：

\[ Q=f(L,\bar{K}) \]

其中，资本为固定要素，劳动力为可变要素，生产处于短期。如果给定产量，我们可以通过生产函数直接计算劳动投入。因此，对于这种情况，分析的目标是找到可能的要素投入区间。我们将通过几何的方式进行回答，并且，通过画图也可以加深对生产函数特征的理解。

在图中，我们画出了三条曲线，分别为：

总产量线（Total Product with respect to Labor, \(TP_L\)）：表示劳动力投入与总产出的关系；
劳动力的边际产量线（Marginal Product of Labor, \(MP_L\)），边际产量大小会受到资本投入的约束。总产量线切线的斜率等于劳动力的边际产量，在总产出线的最大值处，边际产量等于0。

\[ MP_L = \frac{\partial f(L,\bar{K})}{\partial L} \]

劳动力的平均产出线（Average Product of Labor, \(AP_L\)），代表企业的劳动生产率。总产量线上的点与原点连线的斜率代表平均产出。

\[ AP_L = \frac{f(L,\bar{K})}{L} \]

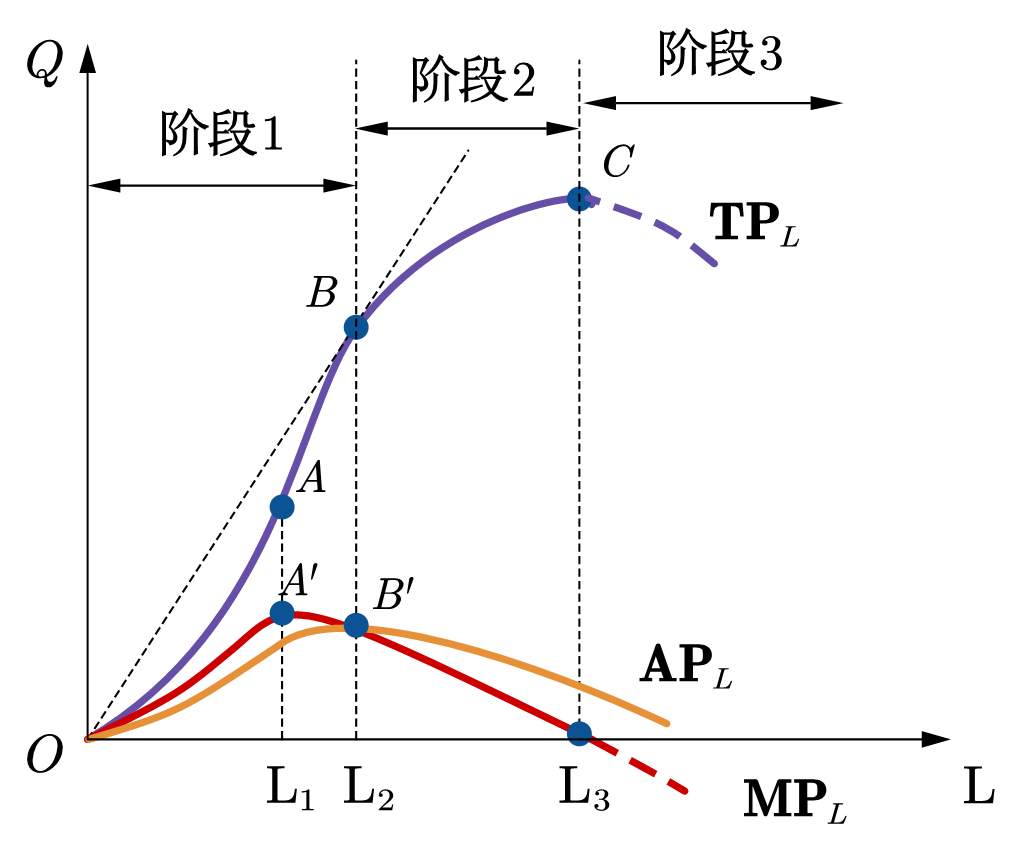
../../_images/L4-production-short-run-curve.png — Fig. 72 短期总产量线、边际产量线和平均产量线。#

图中三条曲线的性状受到边际产量递减规律的约束：

边际产量线呈倒-U形体现的是劳动力的边际产量最终一定是递减的；
边际产量等于总产量线切线的斜率，所以边际产量先增后减对应的是总产出线先凸再凹向横轴，其拐点（A点）对应的是边际产量的最高点；相应的，边际产量等于0时，总产出达到最大值处，边际产量为负时，总产出下降。

因为总产量线（\(TP_L\)）上的点与原点连线的斜率是平均产量，所以总产量线先凸再凹向横轴对应的是平均产出线也为倒-U形。当总产量线上的点（B点）与原点连线恰好相切于总产量线的上方时，平均产量达到最大值，且与边际产量相等，说明边际产量线一定会通过平均产量线的最高点。基于边际与平均的关系，可以得到，当\(L< L_2\)时，平均产量递增，且小于边际产量；当\(L>L_2\)时，平均产量递减，且大于边际产量。

证明：在平均产量的最高点，\(MP_L\) = \(AP_L\)

平均产出的最高点满足条件：

\[ \frac{dAP_L}{dL} = 0 \]

\[\begin{split} \begin{align} &\frac{dAP_L}{dL} = \frac{d(Q/L)}{dL} = \frac{(dQ/dL)L - Q}{L^2} = \frac{MP - AP}{L} = 0\\ &\\ \Rightarrow &MP = AP \end{align} \end{split}\]

接下来，我们将图72中劳动力和产出的关系划分为三个阶段。

阶段1：\(L\in (0, L_2)\) 。其中\(L_2\)表示平均产量最高点对应的劳动投入。在这个阶段，随着劳动投入的增加，边际产量开始增加，并达到最高点后开始降低，但始终高于平均产量，从而使平均产量持续增加。
阶段2：\(L\in [L_2,L_3)\)，其中\(L_3\)表示边际产量为0时的劳动投入。在这个阶段，边际产量持续下降至0，且小于平均产量，从而导致平均产量持续降低。相应的，总产量在\(L_3\)处达到最大值。
阶段3：\(L \geq L_3\)，边际产量为负。总产量和平均产量随着劳动投入的增加持续下降。

首先，企业不会在阶段3进行生产。在这个阶段，劳动力的边际产量为负，这意味着减少投入将会带来更高的产出，因此不使用比使用要好。其次，企业也不会停留在阶段1进行生产。因为平均产量的增加代表着生产效率的提高，增产会降低平均成本，因此企业会持续增产，而不会停留在阶段1。因此，企业的生产决策会选择在阶段2进行，即劳动力的边际产量和平均产量为正且持续下降。具体的投入数量取决于要素和商品的市场价格。阶段1和3可以称为生产函数的非经济的区域（non-economic regions in production function）。

有两种可变生产要素#

当涉及两种可变要素时，企业决策既可以是长期的（仅涉及两种要素投入），也可以是短期的（涉及多于两种要素的投入）。因此，本部分的分析不仅仅限于长期决策，所得出的最优选择条件也适用于涉及多种（超过两种）可变要素的生产决策。

成本最小化问题#

给定产量，企业的成本最小化问题可以表述为：

\[\begin{split} \begin{eqnarray} \min_{L,K}\ wL + rK \\ s.t. \quad f(L,K) = \bar{Q} \end{eqnarray} \end{split}\]

其中，\(\bar{Q}\)为给定的产量，w表示劳动力的单位价格（工资），r表示资本的单位价格（租金）。

之所以用租金（严格来讲，是租用一单位资本的年租金）表示资本价格，是因为很多企业会选择租借使用设备、厂房或其它资本。那么，对于企业自购的资本，价格该如何衡量呢？是否需要和租金有所区别呢？

对于企业自购的资本，其成本可以划分为两部分：

经济折旧：资本在市场上的价格变化（严格来讲，是预期市场上价格的变化，因为未来尚未发生），反映了是企业使用资本的机会成本：
经济折旧 = 期末的市场价格 - 期初的市场价格
为什么不用会计上的折旧方式呢？这是因为会计折旧没有考虑市场的变化，比如，某台设备的计划生命周期是10年，但是如果预期一年后，因技术更迭，相关产品会被市场淘汰，该设备也不能用做它途，那么持有该设备的成本将等于其总价格，而非价格的1/10 （如果采用线性折旧）。
放弃的利息。此处衡量的是企业购买资本支出的利息，因为这些支出可以投到其他地方获益，所以其利息也是使用资本的机会成本。在具体计算时，我们需要剔除既往折旧，使用剩余的支出计算利息。

假设一台新设备的价格为10万元，预期使用1年、2年和3年后的市场价格分别为9万元、8万元和6万元，投资回报为8%。在企业的购买时点，我们可以计算之后三年设备的使用成本：

第一年的成本为1.8万（\( = (10-9) + 10*8\%\)）
第二年的成本为1.72万（\( = (9-8) + 9*8\%\)）
第三年的成本为2.64万（\( = (8-6) + 8*8\%\)）

如果市场是完全竞争的，那么租金和自购的成本是一样。这是因为两者不一致时，企业的资本回报会出现差异，其购买或租赁决策会相应进行调整，哪种方式的回报高，需求增加，价格上涨，最终在均衡时，两者价格会趋同，资本回报相等。因此，我们仍可以使用租金作为资本的价格进行分析。

等成本线#

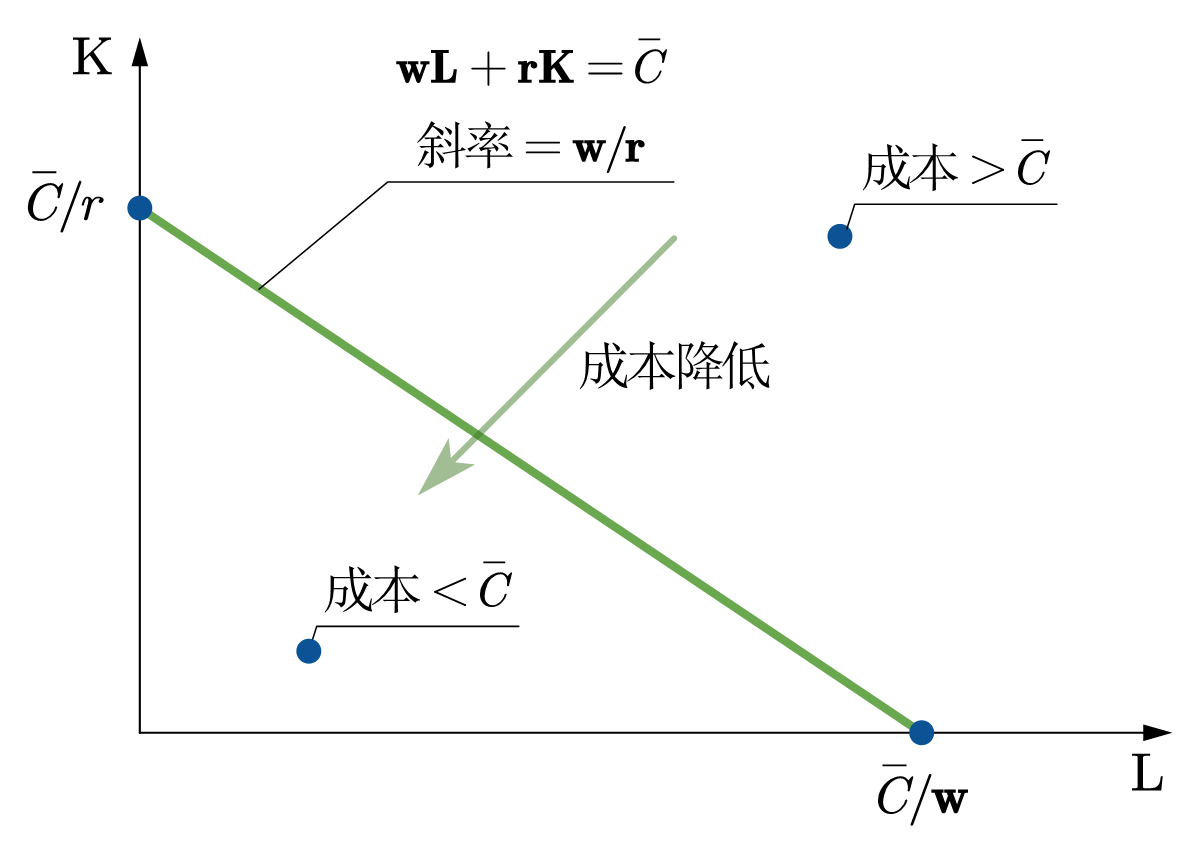
当成本给定时，所对应的那些要素组合的连线就是等成本线，如图73 (a)所示。

(b) 成本最小化问题 — Fig. 73 等成本线和成本最小化问题的最优要素投入#

等成本线斜率的绝对值（\(=\frac{w}{r}\)）代表的是劳动力与资本在市场上的交换比率，即用资本表示的劳动力在市场上的相对价格。等成本线右移代表成本增加，左移代表成本减少。

最优条件#

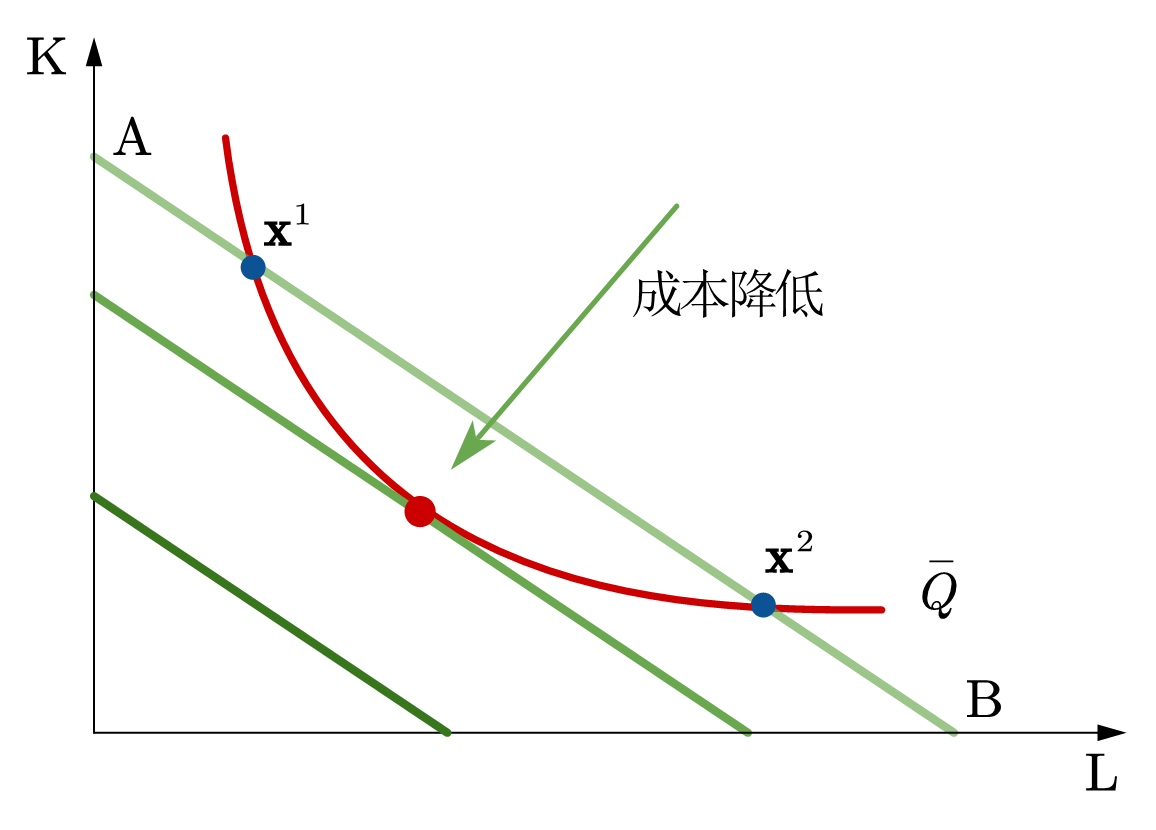
定义等成本线后，我们可以通过几何方式来分析成本最小化问题。具体做法是固定等产量线，移动等成本线，然后寻找在等产量线上的哪个要素组合所对应的等成本线的成本最低，换句话说，离原点越近越好。

接下来我们思考一下最优选择所需要满足的条件。如图73 (b)所示，在要素组合\(\mathbf{x}^1\)和\(\mathbf{x}^2\)为等成本线AB和给定的等产量线的交点，产量都为\(\bar{Q}\),但它们并不是相同产量下成本最低的要素组合。因为如果将等产量线向左移动，成本降低，同时仍可以产出\(\bar{Q}\)单位，直至与等产量线相切。在相切后，如果再向左移动等产量线，将不能产出给定的产量\(\bar{Q}\)。因此，相切便为成本最小化问题的最优条件，即在最优选择处，要素的边际技术替代率等于要素价格之比，其代数表达为：

\[\begin{split} \begin{align} MRTS_{K,L} &=& \frac{r}{w}\\ f(K,L) & = & \bar{Q} \end{align} \end{split}\]

我们将由上式解出的要素最优投入，关于给定产量和要素价格的函数，称为条件要素需求函数。

\[\begin{split} \begin{align} L^* &=& L(r,w, \bar{Q})\\ K^* &=& K(r,w, \bar{Q}) \end{align} \end{split}\]

我们还可以将\(MRTS_{K,L} = \frac{r}{w}\)转化为：

\[ \frac{MP_K}{r} = \frac{MP_L}{w} \]

表明在最优投入下，每种要素所支付的最后一块钱的边际产量相同。我们可以由这个条件写出多种要素投入下的最优条件：

\[ \frac{MP_1}{w_1} = \frac{MP_1}{w_2} = \cdots = \frac{MP_n}{w_n} \]

将满足最优条件——两要素的边际技术替代率等于两者的价格之比——的要素组合相连，所构成的曲线被称为「扩展线」。扩展线上的每一个点都是企业在某一产量下的最优要素投入。显然，扩展线一定是等斜线，等斜线不一定是扩展线。

扩展线与等斜线

扩展线一定是等斜线，等斜线不一定是扩展线。

对偶问题#

成本最小化问题的对偶问题为给定成本的产量最大化问题，即

\[\begin{split} \begin{align} \max_{L,K} f(K,L)\\ s.t. rK + wL = \bar{C} \end{align} \end{split}\]

从几何的角度分析，产量最大化问题可以转化为固定等成本线，移动等产量线的问题——寻找在等成本线上的哪个要素组合对应的等产量线的产量最高。如图74所示，在产量最大化问题中，最优条件仍是相切，即找到一条等产量线与给定的等成本线相切。最优要素投入满足：

\[\begin{split} \begin{align} MRTS_{K,L} &=& \frac{r}{w}\\ wL^* + rK^* & = & \bar{C} \end{align} \end{split}\]

最优要素投入是关于给定的成本和要素价格的函数。

\[\begin{split} \begin{align} L^* &=& L(r,w, \bar{C})\\ K^* &=& K(r,w, \bar{C}) \end{align} \end{split}\]

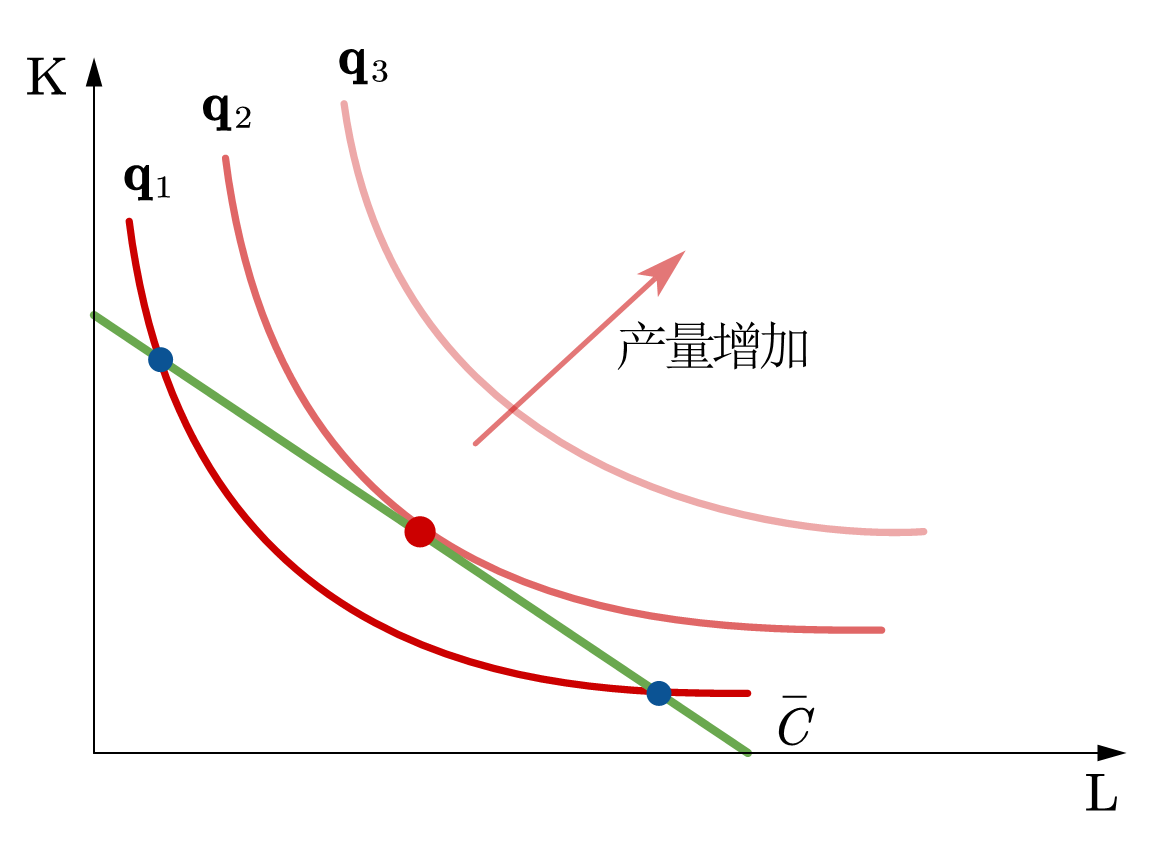
../../_images/L4-production-maxq.png — Fig. 74 产量最大化问题：固定等成本线，移动等产量线。#

考考你

已知某企业的生产函数为\(Q = L^{2/3}K^{1/3}\), 劳动力价格为w=2, 资本价格为 r=1。 (1) 当产量Q=800时，企业实现最小成本时的L, K和C的数量？ (2) 当成本C=3000时，企业实现最大产量时的L, K和Q的数量？

第一问是成本最小化问题：

\[\begin{split} \min_{L,K} 2L + K\\ s.t. L^{2/3}K^{1/3} = 800 \end{split}\]

在最优要素投入处，等产量线与等成本线相切，得到

\[\begin{split} MRTS_{LK} = \frac{w}{r} = 2 \quad (p.1)\\ \end{split}\]

由生产函数，我们可以计算\(MRTS_{LK}\)的表达式：

\[ MRTS_{LK}=\frac{MP_L}{MP_K} = \frac{2/3L^{-1/3}K^{1/3}}{1/3L^{2/3}K{-2/3}} = \frac{2K}{L} \quad (p.2) \]

将(p.2)带入(p.1)中，可得两要素在最优投入处的关系：

\[\begin{split} \frac{2K}{L} = 2\\ \Rightarrow K = L \quad (p.3) \end{split}\]

将(p.3)带入约束条件：

\[\begin{split} L^{2/3}L^{1/3} = 800\\ \Rightarrow L^* = K^* = 800 \end{split}\]

相应的成本为：

\[ C^* = 2L^* + K^* = 1600 + 800 = 2400 \]

第二问是产量最大化问题：

\[\begin{split} \max_{L,K} L^{2/3}K^{1/3}\\ s.t. 2L + K = 3000 \end{split}\]

同样，在最优要素投入处，等产量线与等成本线相切，得到：

\[\begin{split} \begin{align} & MRTS_{LK} = \frac{w}{r} \\ \Rightarrow & \frac{2K}{L} = 2\\ \Rightarrow & K = L \end{align} \end{split}\]

带入约束条件，可得：

\[\begin{split} \begin{align} & 2L^* + K^* = 3L^* = 3000\\ \Rightarrow L^* = K^* = 1000\\ \Rightarrow Q^* = {L^*}^{2/3}{K^*}^{1/3} = 1000 \end{align} \end{split}\]

快速解法：我们可以利用柯布道格拉斯生产函数的性质快速求解，在最优要素投入处，要素的收入（或支出）占比恒定，由生产函数的系数所决定，为要素的指数与所有要素指数之和的比值，即：

\[ wL^* = \frac{2}{3}C \quad rK^* = \frac{1}{3}C \quad (p.4) \]

在第二问中，约束条件为成本，恒定为3000，带入(p.4)可得最优要素投入：

\[ L^* = K^* = 1000 \]

在第一问中，约束条件为产量，恒定为800，令\(C^*\)为产量为800的最小成本，我们可以用\(C^*\)表示最优要素投入，带入(p.4)：

\[ L^* = \frac{1}{3}C^* \quad K^* = \frac{1}{3}C^* \]

带入生产函数，得到：

\[\begin{split} \begin{align} & {\frac{1}{3}C^*}^{2/3}{\frac{1}{3}C^*}^{1/3} = 800\\ \Rightarrow & C^* = 2400\\ \Rightarrow & L^* = K^* = 800 \end{align} \end{split}\]

生产

Contents

生产#