附录#
供需模型模拟#
蛛网模型 (Cobweb Model)#
蛛网模型(Cobweb Model)是经济学中一个有趣的模型,用于解释市场供求关系中的动态过程和价格波动。这个模型揭示了价格和数量之间可能存在的滞后效应和波动性。
在蛛网模型中,我们假设卖方无法预知未来的市场价格,需要基于过去的价格水平提前决定未来的生产数量,即产量决定在他们了解实际的市场价格之前。具体假设如下:
产品从生产到销售存在时滞:产品生产周期较长;
市场信息不灵通,卖方对经济未来变动缺乏理性预期:信息有限造成短视现象;
商品本期供给量由上一期商品的市场价格决定(适应性预期);
产品本身不易储存,必须尽快出售;
基于本期的供给量,本期的商品市场价格由需求决定。
蛛网模型的一个典型应用是农产品市场。如果某一年(t期)天气不佳,导致供给减少。供给减少导致价格大幅上升。当农民意识到价格如此之高时,他们会在下一年种植更多(供给曲线移动回到原来的位置),以满足未来的需求,即在原供给曲线上由t期的市场价格决定t+1期的产量。然而,在t+1期,供给量大于需求量,出现过剩,这会导致价格下降以满足消费者的需求(给定t+1期的产量,价格由需求决定)。由于价格低,农民决定再次减少生产(由t+1期的市场价格决定t+2期的产量),从而再次导致t+2期的价格上升。因为农民是对过去价格的反应,存在着生产调整的滞后性和供需反应的时间差,市场可能会出现价格和数量的不规则波动。
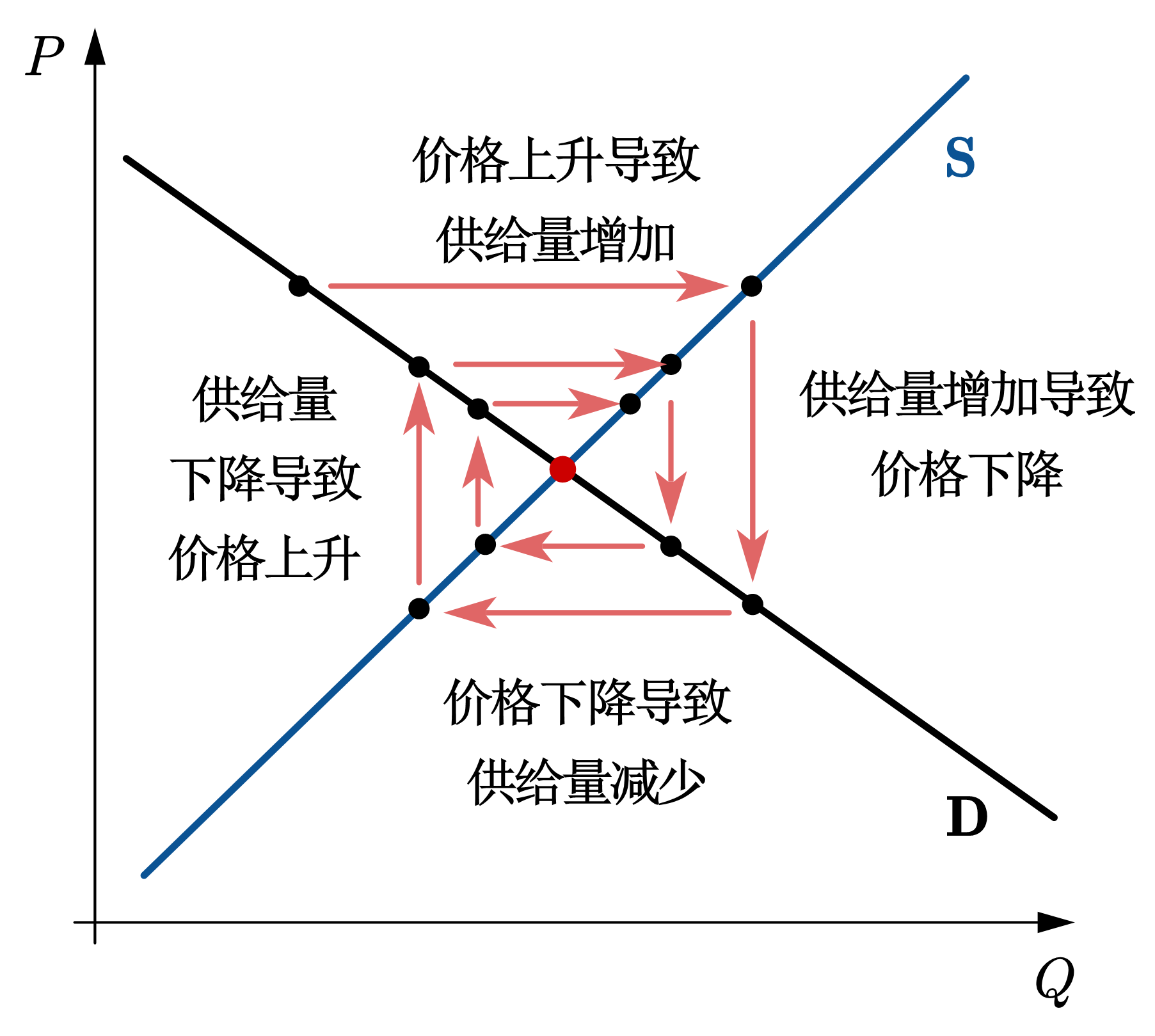
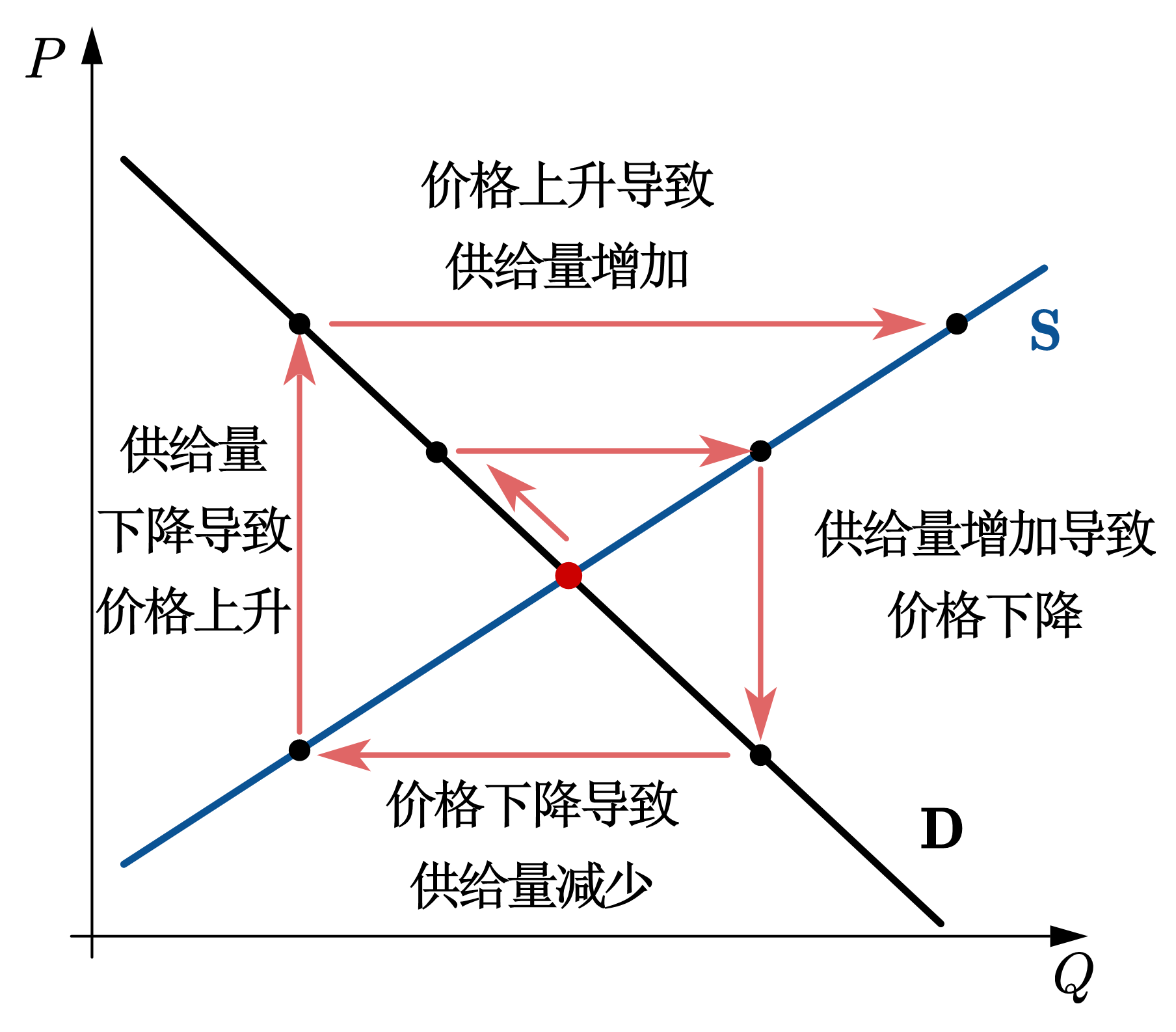
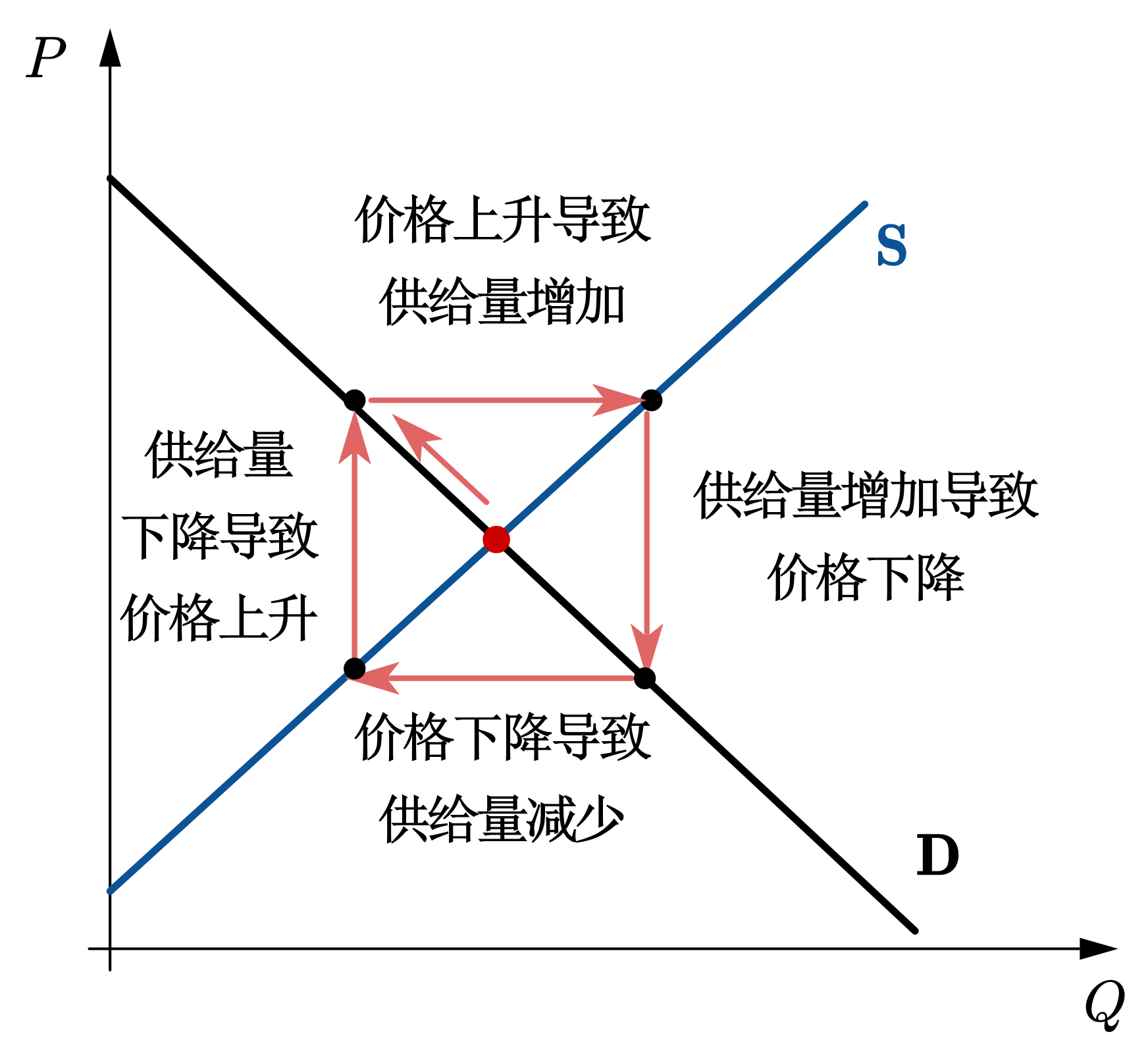
在图43中,我们展示了蛛网模型的四种可能类型。图(a)展示了收敛型(Convergent Fluctuation),需求曲线相较供给曲线更为平坦,即需求曲线斜率的绝对值小于供给曲线的斜率。在这种情况下,当市场在某一期受到外部冲击时,产量将偏离均衡水平,导致价格和产量的波动,最终回到原来的市场均衡。图(b)展示了发散型(Divergent Fluctuation), 需求曲线相较供给曲线更为陡峭,即需求曲线的斜率绝对值大于供给曲线斜率。在这种情况下,当市场在某一期受到外部冲击时,产量偏离均衡水平后,价格和产量的波动逐渐扩大,远离原有的均衡点。图(c)展示的是封闭型(Continuous Fluctuation), 需求曲线和供给曲线的斜率绝对值相等。在这种情况下,当市场在某一期受到外部冲击时,价格和产量按照相同幅度上下波动,循环往复,不会回到原有的均衡点。
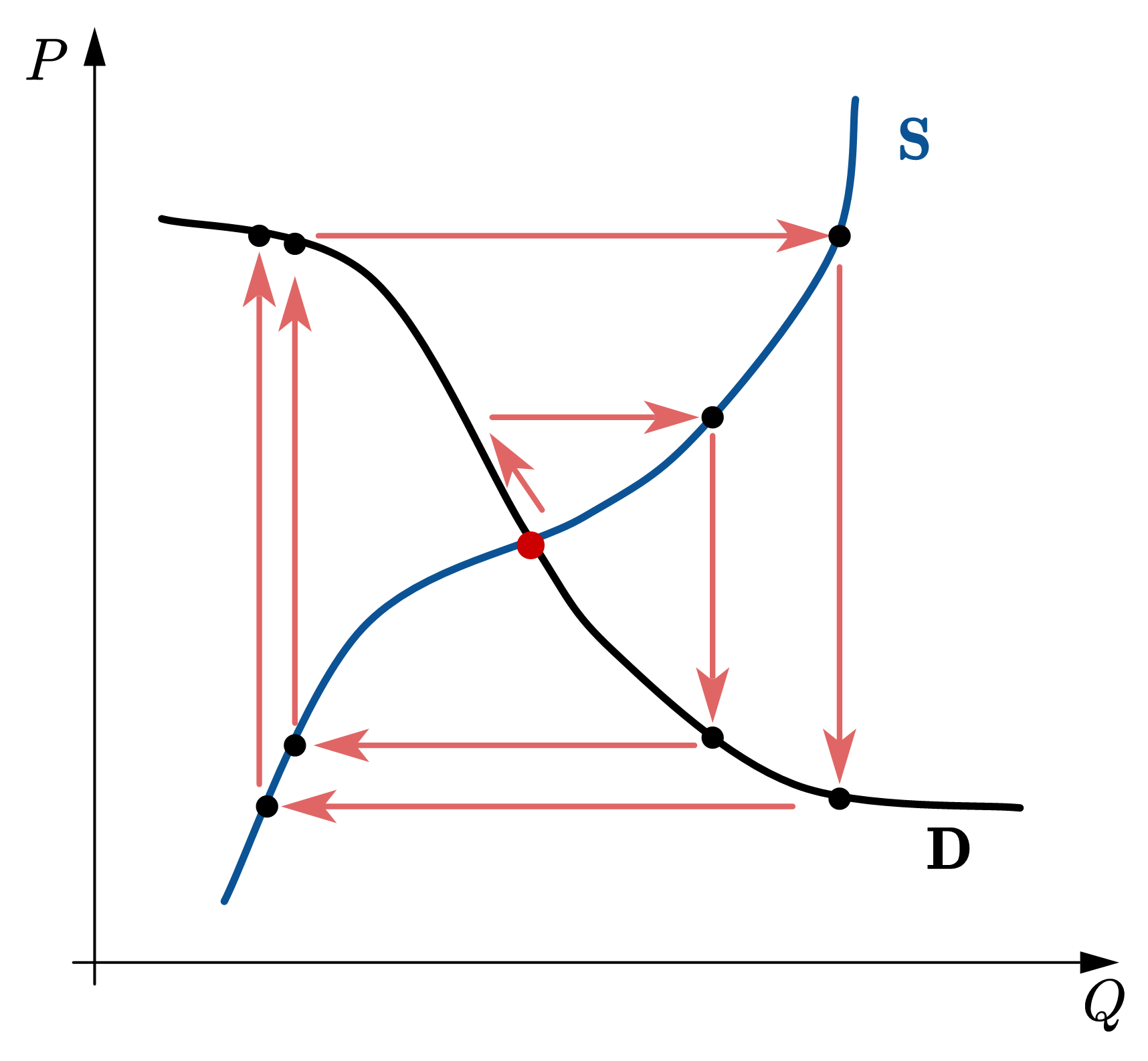
另外还有一种可能的类型,这种类型由曲线的陡峭程度变化所导致:如果在供需曲线的交点附近,需求曲线比供给曲线更陡峭,但当远离均衡时,供给曲线变得比需求曲线更陡峭,我们会得到如图(d)所示的蛛网模型。起初,价格和数量的波动表现为发散。然而,随着供给曲线变得比需求曲线更陡峭,可能会达到一个极限循环,将发散波动转化为封闭型。
Fig. 43 蛛网模型的四种可能类型#
蛛网模型是一个简化的经济模型,假设农民的决策仅基于过去的价格,并忽视了其他因素的影响。现实世界中,市场供求受到更多复杂因素的影响,如政策干预、技术进步和市场竞争等。此外,模型假设农民对价格的反应是适应性预期,而不考虑理性预期的情况。
尽管蛛网模型存在局限性,该模型为我们提供了一种理论框架,用于研究市场行为和价格波动的一些基本机制。通过深入研究和理解蛛网模型,我们能够更好地把握市场的运作和供求关系,以及预期形成对于经济动态的重要性。
蛛网模型的局限性
理性预期问题。模型假设农民基于前一年的价格决定明年的供给,即假设明年的价格将与去年相同(适应性预期)。然而,在现实世界中,这种情况很少发生。农民更可能将其视为“好年份”或“坏年份”,并从价格波动中获得经验教训。
价格发散是不现实的并且在实证中并未出现。只依据去年的价格决定供给意味着理论上价格可能逐渐分散,但农民会从中吸取教训并预先预测价格的变化。
转换供给可能并不容易或可取。一个土豆种植者可能会专注于种植土豆,因为这是他的专长。放弃土豆并转向茄子并不容易。
其他影响价格的因素。影响价格的因素远不止农民的供给决策。在全球市场上,通过进口来减少供给波动。此外,需求可能会变化。此外,供给可能会受天气等因素影响而有所变化。
未考虑库存的影响。政府或生产者可以通过购买过剩产品来限制价格波动,以减轻价格波动。
蛛网模型模拟#
数据取对数:揭示经济现象的隐秘密码#
数据取对数是一种常见的数据处理方法,具有诸多好处。这种转换方法在经济学和统计学中得到广泛应用,可以提供更直观、更可比较的数据分析结果。
首先,取对数可以帮助我们更好地观察和解读增速。宏观经济数据取对数后的时间序列图能够更清晰地展示出增速的变化。以国内生产总值(GDP)为例,我们可以将GDP数据取对数后绘制时间序列图,从中观察到增速的趋势和波动。这种相对差异的呈现方式,使得我们更容易把握经济增长的速度和趋势。
其次,取对数还有助于缩小数据差距,让我们更好地认识数据之间的区别。以个人收入为例,有时我们会发现收入差距相当大,而这种差距对于分析和比较显得不太方便。然而,如果我们将收入数据取对数,就能够有效地缩小差距,更直观地比较不同收入水平之间的差异。这样一来,我们就能够更准确地研究和描述不同收入群体之间的经济现象。
此外,取对数还可以将数据转换为接近正态分布的形式,这对于许多经济和金融领域的数据分析非常有帮助。正态分布在很多统计方法中具有重要的性质和假设。因此,当我们的数据不满足正态分布的假设时,可以通过取对数的方式使其更接近正态分布。这样,我们就能够更准确地运用统计学方法来进行数据分析和推断。
需要注意的是,数据取对数也可能带来一些限制和潜在的问题。例如,取对数后可能丢失了一些绝对数值的信息,因为对数转换将原始数据映射到了一个新的尺度。此外,取对数时需要考虑数据的取值范围和分布特点,以避免引入不期望的结果。因此,在实际应用中,我们需要根据具体情况谨慎选择是否进行数据取对数,并在必要时采取适当的数据预处理和转换方法。