供给#
供给的基本概念都是与需求相对应的。核心点是需要理解,在没有生产的情况下,供给与需求曲线本质是同一条线。
供给和供给量#
供给代表的也是一个价量关系:价格与卖方愿意且能够出售的最大数量的关系。与需求的不同之处在于是从出售的角度看数量。愿意且能够出售的最大数量被定义为供给量,所以供给量可以理解为供给的一个取值。我们也可以说供给是价格和供给量的关系。与需求量相同,供给量也是意图之物,所以若将供给量与现实中的销售量相连,我们也需要一个逻辑上的挂钩。
我们将供给的代数表示称为供给函数,其基本形式为:
其中,\(Q^s\)为供给量,\(P\)为价格。供给函数的反函数称为逆供给函数或反供给函数。
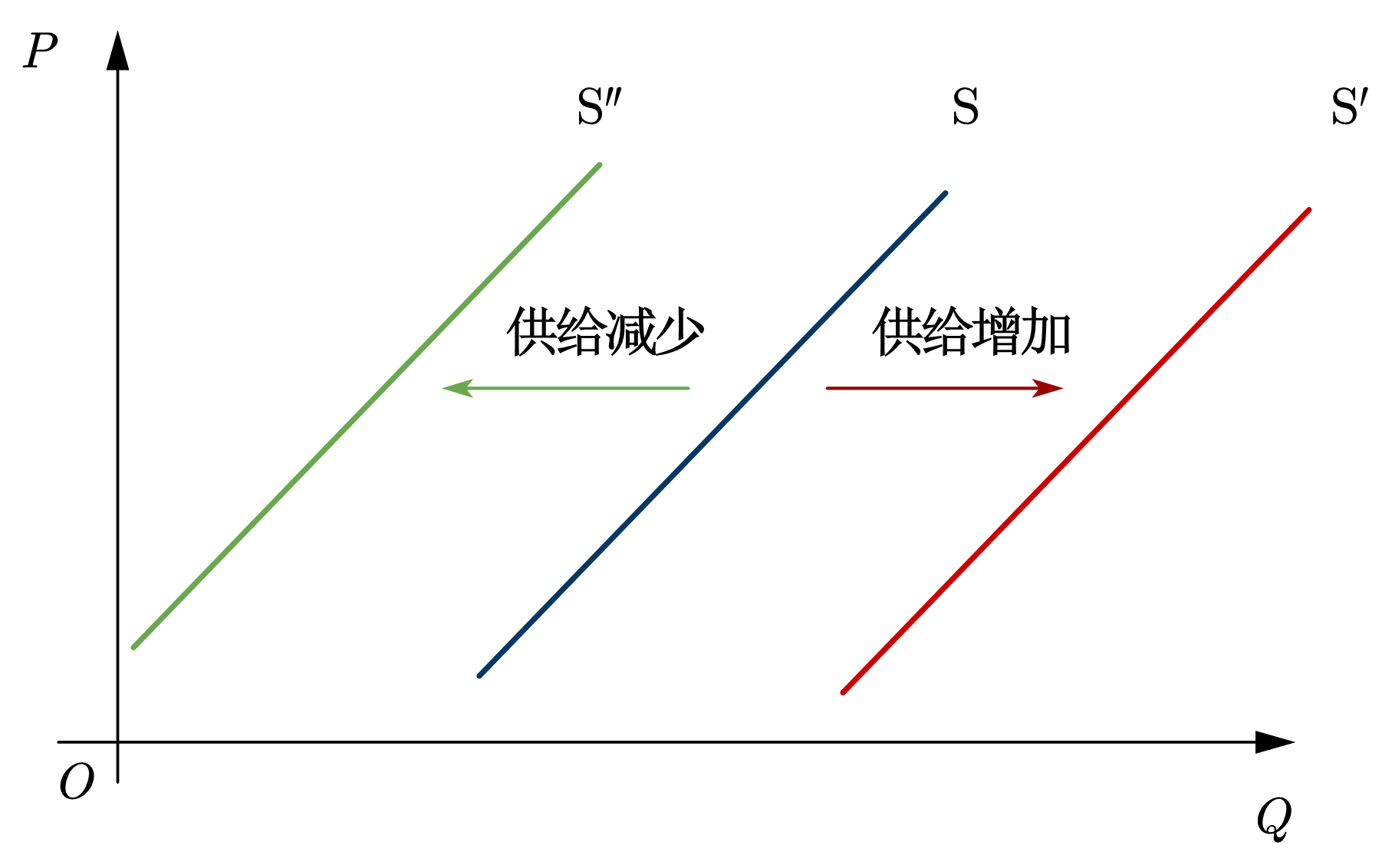
供给的几何表示称为供给曲线,通常用字母S表示,如图18所示。相应的,供给的变化对应的是供给曲线的移动。供给增加(同价下,供给量增加),供给曲线向右移动;供给减少(同价下,供给量降低),供给曲线向左移动。供给量的变化是指在同一条供给曲线上的点的移动。
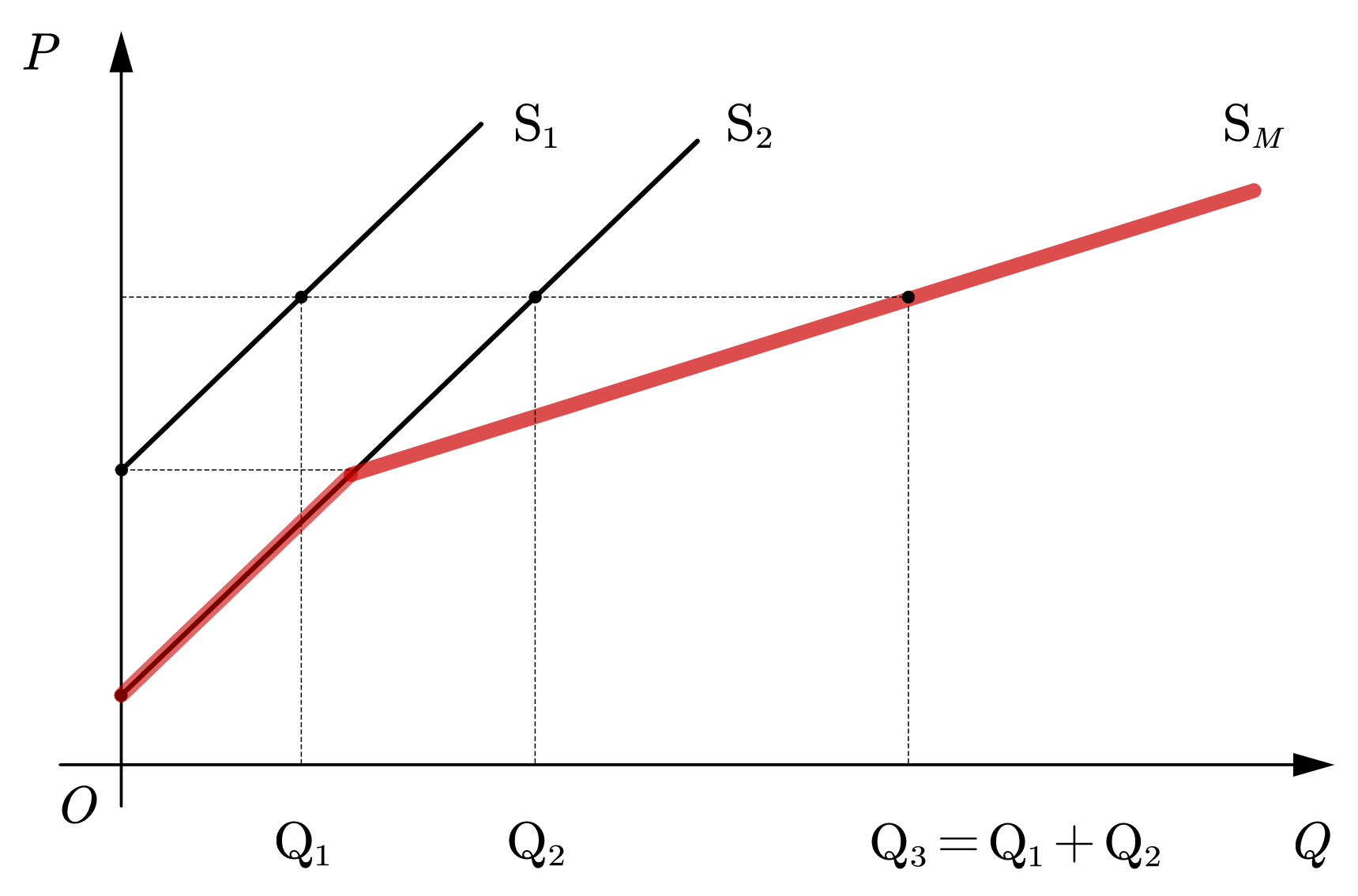
与需求一致,市场供给是个人供给的加总,也即同价下,加量。如图19表现为市场供给曲线是个人供给曲线的横向加总(价格在纵轴)。
其它因素不变的选择#
与需求一样,我们也将与供给相关的因素简单划分为三类。
第一类因素是指在同价下,直接引起供给量变化的因素(Supply shifter),其中包括劳动力工资,原材料价格,生产技术水平,市场上卖方的数量(影响市场供给),以及预期(需要指出引起预期变化的局限条件)等因素。比如,政府对新能源汽车产业的政策支持,改变了汽车制造商的预期,增加了新能源汽车的资本投入,从而使供给增加。
第二类因素是指直接影响价格的因素,如,引起需求变化的因素(Demand shifter),这些因素变化时,需求曲线会发生移动,从而引起商品的价格变化。
第三类因素是指价格对供给量影响的中间因素。
对于供给,其它因素的选择与需求一致:只有第一类因素在同一条供给曲线上不可变。如果这些因素发生变化,我们就需要画一条新的供给曲线描述供给关系。
供给的约束#
我们首先思考一个假想情境。假设世界上不存在生产,小谢对某种商品的资源禀赋(初始拥有量)为\(\bar{X}\)。在每一给定价格p下,小谢对这种商品的(净)需求量可以定义为\(Q^d(p) = X(p) -\bar{X}\),\(X(p)\)为小谢在价格\(p\)下所愿意且能够持有的最大数量,也可称为总需求量。若在价格\(p^0\)下,\(X(p^0) = \bar{X}\), 则(净)需求量\(Q(p^0) = 0\)。
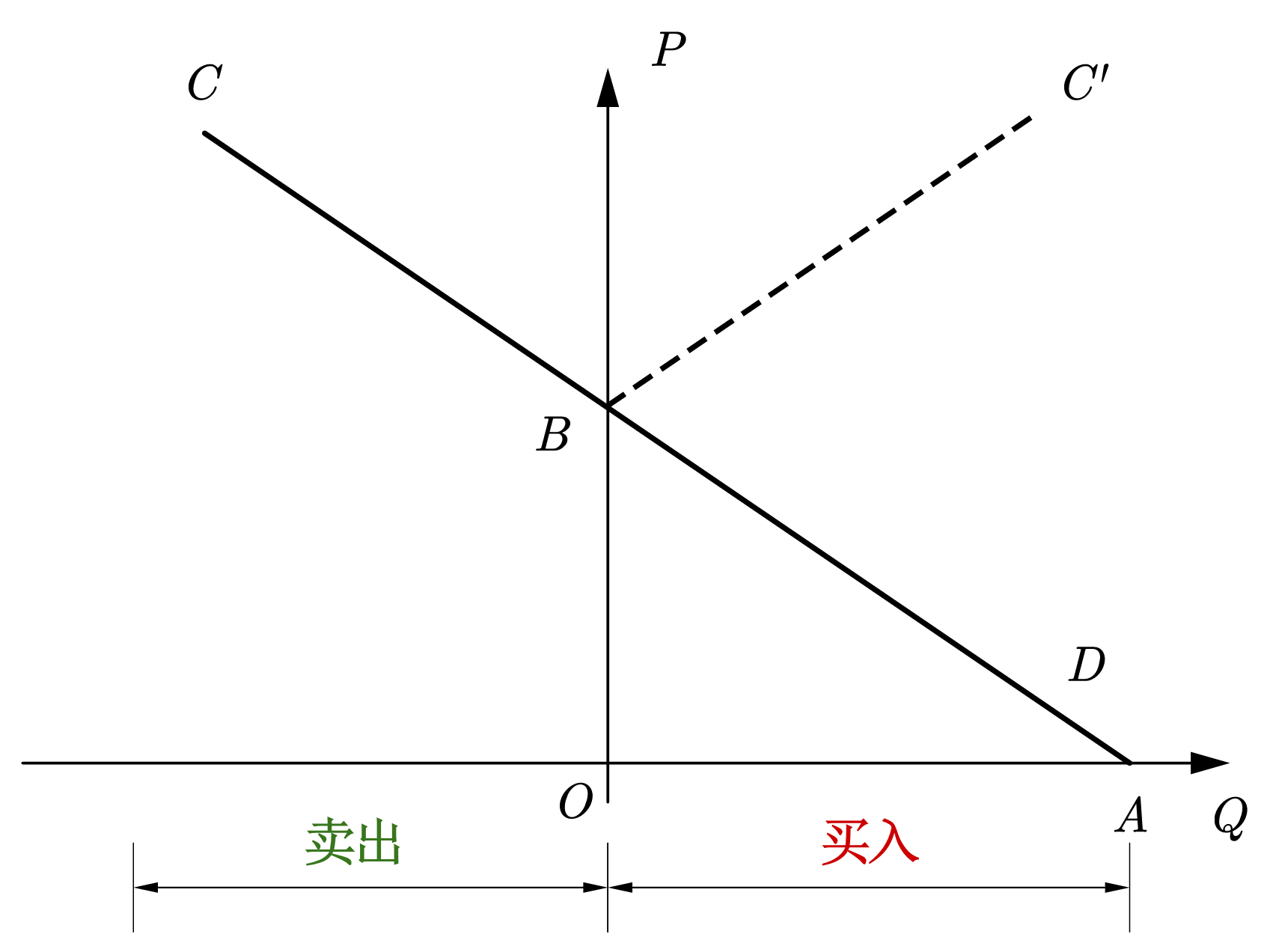
如图%s所示,AC表示小谢的需求曲线,需求定律要求需求曲线向右下方倾斜。AC在第一象限的AB段表示小谢的买入行为(\(X(p)>\bar{X}\)),在第二象限的BC段表示小谢的卖出行为(\(X(p)<\bar{X}\))。换言之,在需求定律的约束下,随着价格的提高,小谢愿意持有的数量越来越少,愿意出售的数量越来越多。在BC段,出售的数量(\(|X(p)-\bar{X}|\))即为小谢对这种商品在某一价格水平下的供给量。为了符合表达习惯,我们将BC段沿着纵轴对称翻转到第一象限,记为\(BC’\),即为小谢对这种商品的供给曲线。可见,供给受需求约束。在无生产的情况下,供给和需求在本质上没什么不同,或者说供给曲线和需求曲线是一条线——在需求定律的约束下,供给曲线向右上方倾斜。
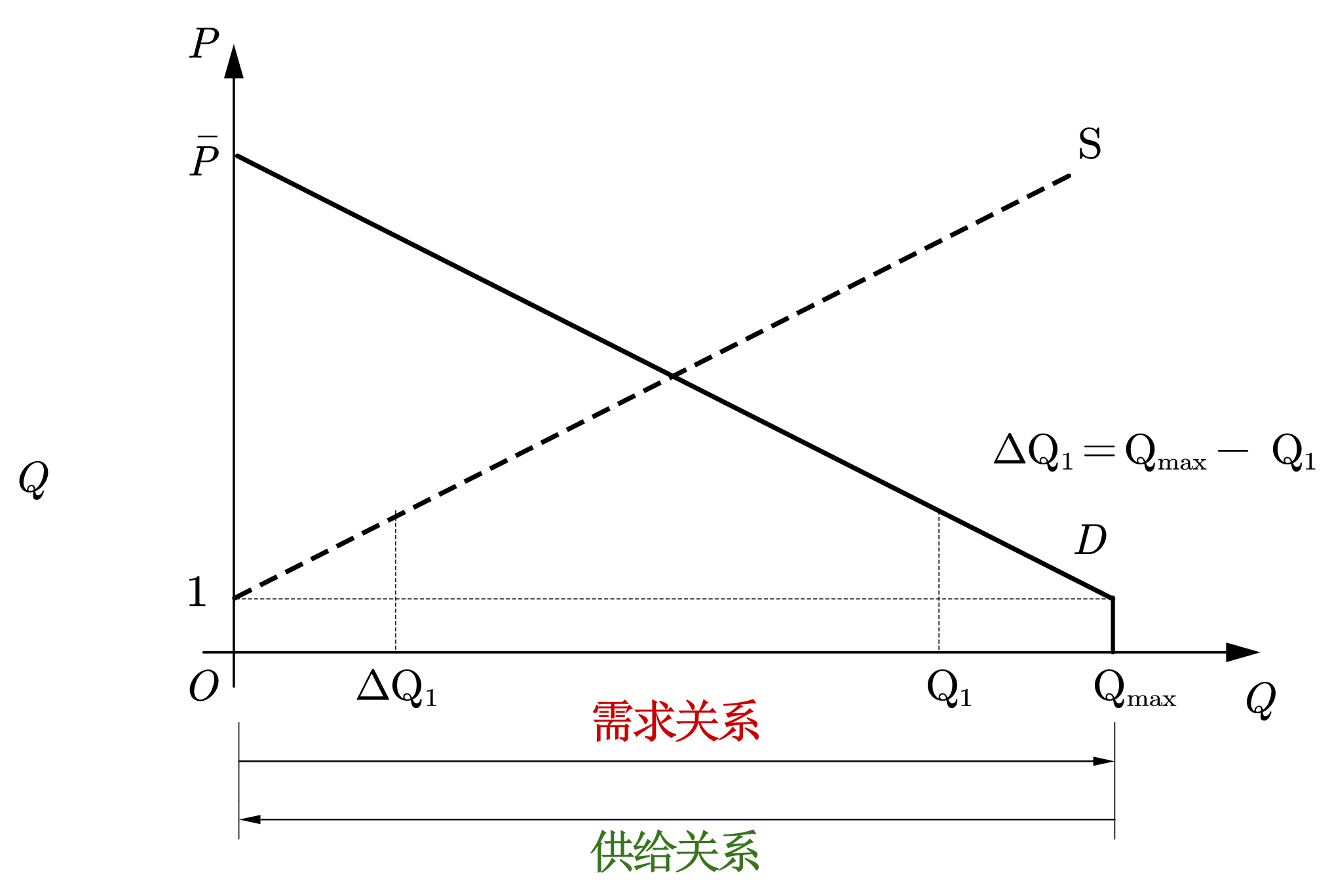
我们再换一个角度进行理解,仍考虑没有生产的世界,假设某商品在价格1元时,小谢愿意持有的数量为\(Q_{max}\),价格在\(\bar{p}(>1)\)时,小谢愿意持有的数量为0。需求曲线如图21所示,当价格由\(\bar{p}\)下降时,小谢会通过购买增加其持有量(需求定律)。反之,当价格由1元上升时,需求量逐渐降低,小谢会选择出售商品,以减少其持有,出售数量为\(Q_{max} - Q(p)\)(\(Q(p)\)为价格为P时的需求量),换言之,若从\(Q_{max}\)向左看,减少的数量即为随价格上升而增加的供给量。若在需求曲线的中点处做一条垂直于横轴的直线,并将需求曲线以此线为轴,水平旋转180度,旋转后的曲线即为小谢对这种商品的供给曲线,在价格为\(p\)时,供给量为\(Q_{max}-Q(p)\),当价格上升至\(\bar{p}\)时,供给量为\(Q_{max}\)。同样,需求曲线向右下方倾斜约束着供给曲线向右上方倾斜——需求和供给曲线本质是同一条线。
上述分析表明一个人是买方还是卖方,是消费者还是供应者,要视价格的高低而定:价格足够低,人们就倾向于买进,价格越低,人们越倾向于多买;价格够高,人们就卖出,价格越高,人们越倾向于多卖。
那么问题来了,为什么价格上升,人们会倾向于多卖呢? 是因为我们想要获得其它商品。那为什么出售可以使我们获得其它商品呢?是因为市场经济的竞争准则是市场价格——价高者得。
之前有讲到,在市场经济中,我们为了获得自己所欲求之物,就需要先提供他人所需以获得收入,即自利先利他。“我供应是为了自己的需求,我需求是因为我有供应”,正因为我供应了,所以可以满足我的需求。这正是萨伊定律的含义:供应会创造自己的需求。因此,供给受需求定律约束根源于以市价作为竞争准则。在此准则下,我们并不需要再提出一个供给定律去约束供给曲线的性状。
这里分析的前提是没有生产,在现实中大部分商品并不是天然存在的,其供给依赖于生产,即供给的背后是生产。在生产部分,我们会分析有生产的供给曲线,但是,由生产所带来的变化并不影响「供应是为了需求」这一结论,需求定律的约束仍是供给曲线的主要内容。
自利利他
《国富论》中有这样一段对「自利利他」的说明:
“我们的一日三餐,不是来自于屠夫、酿酒师和面包师的恩惠,而是由于他们自利的打算。我们不是向他们乞求仁慈,而是诉诸他们的自利之心,从来不向他们谈自己的需要,而只是谈对他们的好处。”
“每个人都在力图应用他的资本,来使其产品能得到最大的价值。一般地说,他并不企图增进公共福利,也不知道他所增进的公共福利为多少。…… 他所追求的仅仅是他个人的安乐,仅仅是他个人的利益。在这样做时,有一只看不见的手引导他去促进一种目标,而这种目标决不是他所追求的东西。…… 由于追逐他自己的利益,他经常促进了社会利益,其效果要比他真正想促进社会利益时所得到的效果更大。我从未听说那些自称为公共利益而从事贸易的人做过多少好事。”
考考你
很多教材会指出劳动供给曲线的形状表现为一条向后弯曲的曲线,即劳动供给曲线中的劳动供给量随着工资上升先增加后逐渐减少。这里我们把工资界定为小时工资,劳动供给量为一定时期内,比如一天,的总工作小时数。人们的时间可以简要划分为工作和休闲两部分(劳动供给量减少等价于休闲需求量的增加)。因为休闲放弃了工作的收入,所以工资可以视为休闲的代价,因此,向后弯曲的劳动供给曲线含义着,当工资高于某一水平后,随着工资的上升(休闲代价的上升),休闲的需求量也会增加,出现价量齐升的现象,请问这是否违反了需求定律?
答:我们可以先思考是否有其它情况发生了变化。在一天之内,人们的工作时间存在上限——不能超过24小时,并且无法在没有休息的情况下持续满额工作,否则身体健康会极度受损。通常而言,工资上升,工作强度也会相应增加,劳累对身体健康会产生负面影响,在这种情况下,增加对休闲的需求,使休闲的需求曲线向右移动,而非在同一条需求曲线上进行分析。
或者,我们也可以考虑休闲真正的代价是什么,或者说工作真正的收益是什么。工作除了获得工资外,还有健康的影响,当工作强度增加,上升的工资可能无法抵消身体健康的受损,带来真正收益的下降——休闲真正的代价下降,需求量上升,符合需求定律。