附录:对因果关系的探寻#
Knowledge is the object of our inquiry, and men do not think they know a think till they have grasped the “why” of it (which is to grasp its primary cause)
—Aristotle
在因果发现中,很多时候不能简单地根据事件的发生顺序,确定因果关系。例如气压计的水银柱下降和下雨概率增加相关,并且水银柱的下降要早于下雨,但是事实是两者之间并不存在因果关系,他们之间的相关性是由于大气压降低同时造成了水银柱的下降和下雨。而且很多数据可能不包含时序信息,比如独立同分布的静态数据。
原因是什么? 迄今,对于原因,仍没有一个确定性的定义,哲学界也没有公认的关于因果关系的理论。
休谟指出原因和结果之间应存在规律性。但是,很多因果关系并不是必然发生的,原因可能既不是结果的充分条件,也不是必要条件(原因发生,结果不一定发生;结果发生,也不一定是源于提出的原因)。比如,上大学就会找到好工作(假设“好”可以被量化),这里的因果关系就是不确定的。因此,有学者建议使用概率来定义因果关系:原因可以提高或增加某种结果出现的可能性。但是,某些非原因的事物也可能会提高结果出现的概率,从而导致错误的判断。
也有学者建议使用反事实推理法定义因果关系,即“通过假设导致某件事的原因不存在,事情的发展会有何不同,从而界定事件发生的原因” ([], p122) 。在现实中,原因发生与没有发生的结果只能观察其一,所以这相当于是在平行世界中观察结果的走向。假设,我们认为A是B的原因,其暗含的推理逻辑是:
如果A没有发生,B不会发生
这里,A是B的必要条件。需要注意的是,对比A发生或没发生的影响时,需要保证其它影响B的条件都不会发生变化,即其它条件不变。反事实推理是建立因果推断的重要思想,如,[]的Potential outcome framework便是基于反事实推理研究因果推断。该框架在经济学中有着广泛的应用。再如,[]将反事实诊断算法(将诊断形式化为反事实推断任务)应用到医疗诊断中,其研究结果表明因果推理是将机器学习应用到医疗诊断中的重要缺失元素。
反事实推理的问题在于,如果导致结果的原因有很多,使用反事实推理法可能会无法确定具体的原因。此外,我们也可能会将距离实际结果越来越远的事件作为原因。比如,小谢今天之所以没有来上课,是因为小张叫她去打游戏;小张之所以会找小谢打游戏,是因为她考试没考好,心情郁闷;小张之所以考试没考好,是因为她复习的时候,发现白宇的新剧《乔家的儿女》上映了,所以迫不及待的追了一下;之所以小张会去看连续剧,是因为白宇是主角。因此,我们推出,如果白宇没有出演《乔家的儿女》,小谢便会去上课。
简言之,无论如何定义原因,总会有例外的情况出现。在此,我们使用[]对原因的描述:原因“一般是指它使某种结果更有可能出现,并且没有它某种结果就不会出现或者无法出现,或者说它能够在适当的环境下产生某种结果”([],p5)。
虽然原因无法被严格定义,但是研究因果关系却非常有现实意义——只有知道为什么,才能更好的预测、解释和干预。然而,因果关系并不能被观察,可以在现实中观察的是(事物之间的)相关关系。而相关关系却不一定含义着因果关系。比如,有研究表明获诺贝尔奖的人数(每千万人)和人均巧克力消费量具有显著的正相关关系,如果从中得出「巧克力有助于获得诺奖的结论」会不会觉得十分滑稽呢?
相关性不等于因果性#
相关性是指变量的变化是有关联的 (associate),或者说,一个变量发生的变化与另一个变量发生的变化是有关联的。关联有可能是正向的,也可能是负向的,比如,儿童的身高和体重正向关联,通胀率和失业率负向关联。
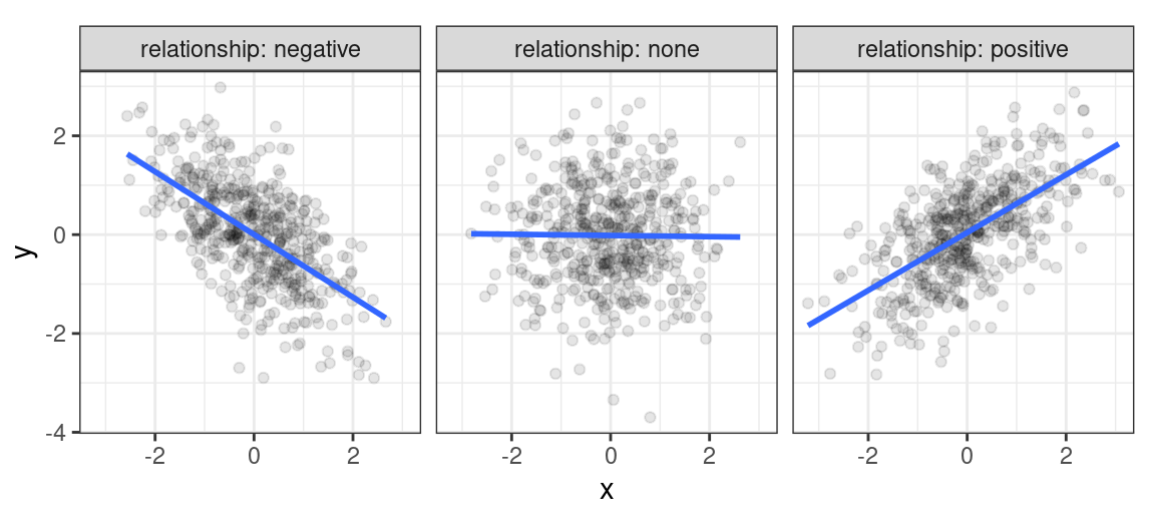
Fig. 8 相关关系#
通常,我们使用皮尔逊相关系数(Pearson correlation coefficient),\(r_{XY}\),作为变量\(X\)与\(Y\)相关性的测量: $\(r_{XY} = \frac{cov(X,Y)}{\sigma_X*\sigma_Y} =\frac{\sum_{i=1}^n(X_i - \overline{X})(Y_i - \overline{Y})}{\sqrt{\sum_{i=1}^n(X_i - \overline{X})^2}\sqrt{\sum_{i=1}^n(Y_i - \overline{Y})^2}}\)$
\(r_{XY}\)一定是在\(-1\)与\(1\)之间(\([-1,1]\)),并且衡量的是变量之间的线性关系。因此,若变量之间不是线性关系,有可能会出现相关性强但相关系数却低的情况。
线性无关不代表没有相关性
假设变量\(x\)和\(y\)的关系和取值如下所示:
\(y = 10 + 40x - x^2\)
\(x\in[0,40]\)
\(\Rightarrow r(x,y) = 0.00\)
这里\(x\)和\(y\)的相关系数为0,但是两者具有相关性。
相关性是对称的(\(r(x,y) = r(y,x)\)),而因果关系却不一定如此。因果关系有可能是单向的,比如,水污染会使人生病,但生病不是水污染的原因。
当观察到变量A和B存在相关关系时,它们的真实关系有可能是:
A和B存在单向的因果关系
A和B存在双向的因果关系,比如,经济发展促进金融发展,金融发展反过来又促进经济发展
其它变量引起A和B的变化,比如,夏天冰激凌销量和游泳池溺死的人数呈正相关关系,其共同的原因可能是因为天气。其它变量通常被称为混淆变量(Confounder),它混淆了变量A与B之间的相关性。
A和B没有任何关系,即A和B是虚假的相关。它们出现相关性可能仅仅是因为巧合,数据被污染,或者分析不当。
虚假的相关
check:revise 当两个随机变量样本量很小时,也有可能会出现相关性,但两者无任何关联。假设有两个服从均匀分布的独立的变量,当样本数量较小时,变量间出现了较强的相关性:
Pearson correlation coefficient:
样本量 = 10 : -0.64
样本量 = 100 : 0.04
样本量 = 1000 : 0.04
样本量 = 10000: 0.00
python 代码:
import numpy as np
np.random.seed(10)
# get two random number and calculate their correlation coefficient; size: sample size
def get_r(size):
ab = np.random.rand(2,size)
return np.corrcoef(ab)[0,1]
sample_size = [10,100,1000,10000]
print('Pearson correlation coefficient:')
for i in sample_size:
print('Sample_size = {:<5d}: {:.2f}'.format(i, get_r(i)))
因此,相关性不代表因果性,仅凭相关性,我们无法知道事物的运行机制,也便无从进行干预。虽然相关性可能会帮助我们做出一些成功的预测,但是这本质是归纳法,归纳法的问题表明我们永远无法确定预测的正确性——预测有可能会失败。
那么,因果关系含义着相关性吗?即,相关性是因果关系的必要条件吗?很遗憾,这也是不一定,比如,跑步有助于减肥,但同时跑步也会促进食欲,不利于减肥,这两个影响恰好方向相反,相互抵消,因此,没有观察到跑步与减肥的相关性,不代表两者没有因果关系。再如,若因果关系是非线性的,则没有线性的相关关系,不一定代表没有因果关系。
相关关系既不是因果关系的必要条件,也不是充分条件。
穆勒五法#
穆勒“五法”是寻找因果关系的五种逻辑方法或思维方式,核心是如何通过观察来探寻原因。此方法是由英国哲学家约翰·穆勒在19世纪所提出的。虽然在现实中,因果关系的不确定性与复杂性会削弱穆勒“五法”的适用性——依据“穆勒五法”得到的结论不一定为真,但穆勒“五法”仍不失为一个直觉式的探寻因果关系的思维模型,适合我们在日常生活中使用。
契合法#
契合法,又称为求同法,即原因有可能是出现相同结果的事件之间的共同点。此方法不意味着有因必有果,存在原因并未导致结果出现的情况,因此,原因是结果的必要条件而非充分条件——结果出现,仅当有这个原因(有果必有因)。
很多传染病的溯源便是基于契合法。比如,John Snow研究1854年伦敦爆发的霍乱发现,很多死亡病历都发生在某个特定的地理区域,并且都靠近宽街(Broad Street)的水泵。在远离宽街水泵的死亡案例中,Snow发现,这些死者大多数都可能引用过那里的水。因此,他推断出宽街(Broad Street)水泵被污染是导致霍乱爆发的原因。
假设用a表示被研究现象(结果),对出现a的不同对象或事件列出相关的现象,每个现象用一个大写字母表示,契合法可用下列公式表示:
对象1:A H C D E a
对象2:A B K O P a
对象3:A B I M N a
对象4:A B U S Z a
对象5:A K P X \(\lnot\)a
通过寻找不同对象的共同点,可以判断A可能是a的原因。并且通过契合法找到的可能的原因不一定只有一个,如果对象2-4也都有B条件,那么B也是可能的原因。契合法中,不考虑对象5出现了A,但却没有出现结果a的情况。
差异法#
差异法又称为求异法(求异除同),即,在其它条件都相同的情况下,原因是出现被解释现象和没有出现被解释现象事件之间的差异点。此方法含义着有因必有果——如果原因出现,则结果必然出现,因此,原因是结果的充分条件(有可能存在其它导致结果的原因)。
这可以理解为是反事实推理在现实中的一种应用,因为我们不可能观察到,同一个对象既受某一现象影响又不受该现象影响的结果——两者只能观察到其一,所以,我们便用其它对象在另一种现象下的结果作为反事实估计。
差异法可用下列公式表示:
对象1:A B C D E a
对象2:A B C D E a
对象3:A B C D E a
对象4: B C D E \(\lnot\)a
可以判断A是a出现的原因。
契合差异并用法#
契合差异并用法又称为并用法,是将契合法和差异法结果起来使用,即原因是结果的充分必要条件:有因必有果,有果必有因。契合差异并用法的基本思路是:如果出现某个被解释现象(结果)的事例中有一个共同的因素,而这个因素未出现在没有该现象的事例中,则这个因素可能就是导致现象的原因。契合差异并用法与差异法的区别在于不要求其它条件都相同。
假设某些地方甲状腺病高发。医疗队发现病区的共同点是居民的食物和水中缺碘(“契合法”) ;而在非病区发现那里的食物和水中不缺碘(“契合法”)。再通过求异法,可以推出缺碘可能是甲状腺疾病的原因。再如,塞美尔怀斯提出的仰卧分娩、传教士摇铃等假说,本质上使用的就是契合差异法。
共变法#
共变法认为原因和结果之间存在剂量效应:随着原因剂量的增加,结果的剂量也随之变化,或者说,在其他条件不变的情况下,如果某一现象发生变化另一现象也随之发生相应变化,那么,前者可能就是后者的原因。差异法可以理解为是共变法的特例——只有两种情况下的共变法。
共变法的问题在于如果因果关系是非线性的,比如,当剂量超过某一个量值后,对结果的影响会减弱或相反变化,那么这时,共变法将无法恰当的识别因果关系。
剩余法#
剩余法是指如果某一复合现象是由某种复合原因引起的,那么,在排除已知的因果关系后,剩下的原因部分就是余下的结果部分的原因,或者说,把已确认有因果联系的部分剔除后,剩余部分也必有因果联系。
但是,如果各个原因会相互作用,那么,剩余法便无法找到真正的因果关系。
比如,詹森(法国天文学家)和罗克耶尔(英国天文学家)在研究太阳光谱时发现了一条红线、青绿线、蓝线和黄线,前三者是氢的光谱,而第四种未知。依据剩余法:一定存在一种新物质导致第四种光线。詹森和罗克耶尔将之称为氦。
