弹性#

之前我们谈需求量或供给量的变化时，都是定性的分析价格或其它因素的变化会如何对它们产生影响。而弹性（Elasticity，E）是定量的衡量一个经济变量（\(X\)）会如何影响另一经济变量（\(Y\)），基本公式为：

\[ E = \frac{\Delta Y / Y}{\Delta X/X} \]

其中，\(\%\Delta Y\) 表示 \(Y\) 的相对变化，\(\%\Delta X\) 表示 \(X\) 的相对变化。含义着当\(X\)变化1%时，\(Y\)会变化百分之几，即\(Y\) 对 \(X\) 的相对变化的敏感程度。弹性没有单位，不会受到分子、分母单位不同的影响。在计算弹性时，除了X外，其它影响Y变化的因素需要保持不变，否则Y的变化就会包含了其它因素的影响。

如果变量之间存在单向影响，那么便可以定义相应的弹性。换句话说，我们可以通过改变弹性公式中\(X\)和\(Y\)变量的含义，来计算不同类型的弹性。例如，我们可以计算消费者价格指数（CPI）对大豆价格的弹性（分母是大豆价格变化的百分比，分子是相应CPI变化的百分比）。在本部分，我们将\(Y\)限定为需求量（\(Q^d\)） 或供给量（\(Q^s\)），并介绍与之相关的五类弹性：

  • 需求的价格弹性：

    \[E_d = \frac{\Delta 𝑸^𝒅/Q}{\Delta P/P}\]

    其中，\(P\)表示价格，\(Q^d\)表示需求量。

  • 需求的交叉价格弹性：

    \[E^d_{12}=\frac{\Delta 𝑸_1^𝒅/Q^d_1}{\Delta P_2/P_2}\]

    其中，\(𝑸_1^d\)和\(P_2\)分别表示商品1的需求量和商品2的价格。

  • 收入弹性 ：

    \[E_{M}=\frac{\Delta 𝑸^𝒅/Q}{\Delta I/I}\]

    其中，\(I\)表示收入。

  • 供给的价格弹性：

    \[E_d = \frac{\Delta 𝑸^s/Q}{\Delta P/P}\]

    其中，\(Q^s\)表示供给量。

  • 供给的交叉价格弹性：

    \[E^s_{12}=\frac{\Delta 𝑸_1^s/Q_1}{\Delta P_2/P_2}\]

    其中，\(𝑸_1^s\)和\(P_2\)分别表示商品1的供给量和商品2的价格。

税收的收入弹性

税收的收入弹性是指税收收入对于经济收入变化的敏感程度。换句话说，它衡量了税收收入在经济总收入变动下的变化幅度。收入弹性通过衡量税收收入对经济波动的反应来评估税收制度的稳定性和可靠性。

税收收入弹性= 税收增长率/经济增长率

其中，经济济增长率，一般使用国民生产总值（GNP）增长率，国内生产总值（GDP）增长率，国民收入（NI）增长等指标衡量。

弧弹性与点弹性#

弧弹性#

由弹性基本公式计算的弹性称为弧弹性，即弹性等于\(Y\)与\(X\)变化的百分比之比。

比如，某种商品的价格由250元下降至200元时，需求量相应地由8单位增加到12单位，我们可以计算这个变化所对应的需求的价格弹性为：

\[ E_d = \frac{(12-8)/8}{(200-250)/250} = -2.25 \]

而如果该商品的价格由200元上升至250元时，需求量由12单位下降到8单位，我们也可以同样计算弹性为：

\[ E_d = \frac{(8-12)/12}{(250-200)/200} = -0.75 \]

虽然价量的变化区域相同，但计算出的弹性值却会受到变化方向的影响，这显然不是一个令人满意的特征。之所以会出现这样的问题，是因为变量变化百分比的计算是以初值或起点值作为分母，即

\[ 变化\% = （末值 – 初值）/初值 *100% \]

为了避免起点选择对弹性计算的影响，我们通常会使用中间值方法计算弧弹性。其思路是将变量变化百分比的计算调整为以初值和末值的中间值作为分母，即，

\[ 变化\% = （末值 – 初值）/中间值 *100% \]

其中，中间值 = （末值+初值）/ 2。

例如，在上例中，使用中间值方法计算的弹性为：

\[ E_d = \frac{(12-8)/10}{(200-250)/225} = -1.8 \]

点弹性#

在弹性的基本公式中，当\(X\)的变化量趋向于0时，我们可以用导数表示弹性，称之为点弹性：

\[ E = \lim_{\Delta X \rightarrow 0} \frac{\Delta Y/Y}{\Delta X/X} = \frac{dY/Y}{dX/X} = \frac{dY}{dX}\frac{X}{Y} \]

我们通常所说的弹性指的便是点弹性，点弹性还可以表示为：

(1)#\[ E=\frac{dY/Y}{dX/X} = \frac{d \ln Y}{d \ln X} \]
证明
\[ \frac{d \ln Y}{d \ln X} = \frac{\frac{d\ln Y}{dY}{dY}}{\frac{d\ln X}{dX}{dX}} = \frac{dY/Y}{dX/X} \]

如果\(X\)和\(Y\)的关系可以用幂函数表示，如\(Y=aX^b\), 其中，\(a,b\neq 0\)是参数，那么，应用式(1)，可以快速计算出\(Y\)对\(X\)的弹性：

\[\begin{split} \begin{align*} Y=aX^b & \\ \Rightarrow \quad & \ln Y = \ln a + b \ln X\\ \Rightarrow \quad & E = \frac{d \ln Y}{d \ln X} = b \end{align*} \end{split}\]

因此，如果\(X\)和\(Y\)的关系可以表示为幂函数，则\(Y\)对\(X\)的弹性为定值，全完由\(X\)变量的指数决定，不随变量取值的变化而变化。通过取对数计算弹性有很强的应用价值，在实证分析中，我们可以通过对变量取对数，做线性拟合去估计相应的弹性。

而如果\(X\)和\(Y\)是线性关系，如\(Y=aX+b\), 其中，\(a,b\neq 0\)是参数，那么，\(Y\)对\(X\)的弹性则点点不同：

(2)#\[\begin{split} \begin{align*} Y=aX+b & \\ \Rightarrow \quad & \frac{dY}{dX}\frac{X}{Y} = a*\frac{X}{Y}\\ \Rightarrow \quad & E = a*\frac{X}{Y} = a*\frac{X}{aX+b} \end{align*} \end{split}\]

弹性分类——按取值划分#

我们可以将弹性依据不同的取值划分为三类：

富有弹性，\(|E|>1\)#

\(|E|>1\)表明当X变化1%时，Y变化百分比的绝对值会大于1%。比如，在美食广场，对于拥有大量同质品的小吃而言，通常会富有需求的价格弹性——价格提高，消费者会转而去购买其它家的小吃。

其中一种极端的情况为\(|E|=\infty\) ，被称为完全弹性。若需求的价格弹性为完全弹性，则需求曲线为固定在某一价格水平下的水平线（价格在纵轴），表示当价格高于这个固定价格时，需求量变为0。

单位弹性，\(|E|=1\)#

\(|E|=1\)表明当X变化1%时，Y变化百分比的绝对值也等于1%。我们可以证明在需求曲线的中点处，其需求的价格弹性为单位弹性。

缺乏弹性，\(|E|<1\)#

\(|E|<1\) 表明当X变化1%时，Y变化百分比的绝对值小于1%。其中一种极端的情况为\(|E|=0\) ，被称为完全无弹性，即X的变化不会引起Y的变化。仍考虑需求的价格弹性，完全无弹性对应的需求曲线为固定在某一数量下的垂线（价格在纵轴）。

以电力市场为例，美国加州的电力市场分为批发市场和零售市场，批发市场的参与者为电网（买方）和发电站（卖方），批发市场的价格为每小时定价。在零售市场，电网将电出售给居民，企业等部门，零售市场的电价受到政府管制，不能由电网随意调整。因此，在短时间内，如果批发市场的电价大幅上涨，电网由于无法调整零售电价影响消费端的用电行为，所以可以认为其对批发电价的反应接近于完全无弹性。

五类弹性——以X、Y划分#

需求的价格弹性#

需求的价格弹性（简称为价格弹性）衡量的是商品的价格变化对消费者需求量的影响，即在同一条需求曲线上的价量关系:

\[ E_d = \frac{dQ^d/Q^d}{dP/P}=\frac{d\ln Q^d}{d\ln P} <0 \]

需求定律要求价量呈反方向变化，所以需求的价格弹性为负值。有些书上将需求的价格弹性定义为上式的绝对值，\(|\frac{dQ^d/Q^d}{dP/P}|\)，但是，需求定律在现实中是需要被检验的，将其定义为正值会淡化其在现实中出错的可能性，因此，我们在此不使用取绝对值的方式定义价格弹性。假若某种商品的价格上升\(5\%\)，需求量相应下降\(10\%\)，则需求的价格弹性为 \(-2\)。

如图27所示，对于通过同一个点，A，的两条需求曲线，若价格由\(p_1\)上升至\(p_2\)，需求曲线越平坦，需求量下降的幅度越大，即对价格变化的反应越灵敏，越富有需求的价格弹性。

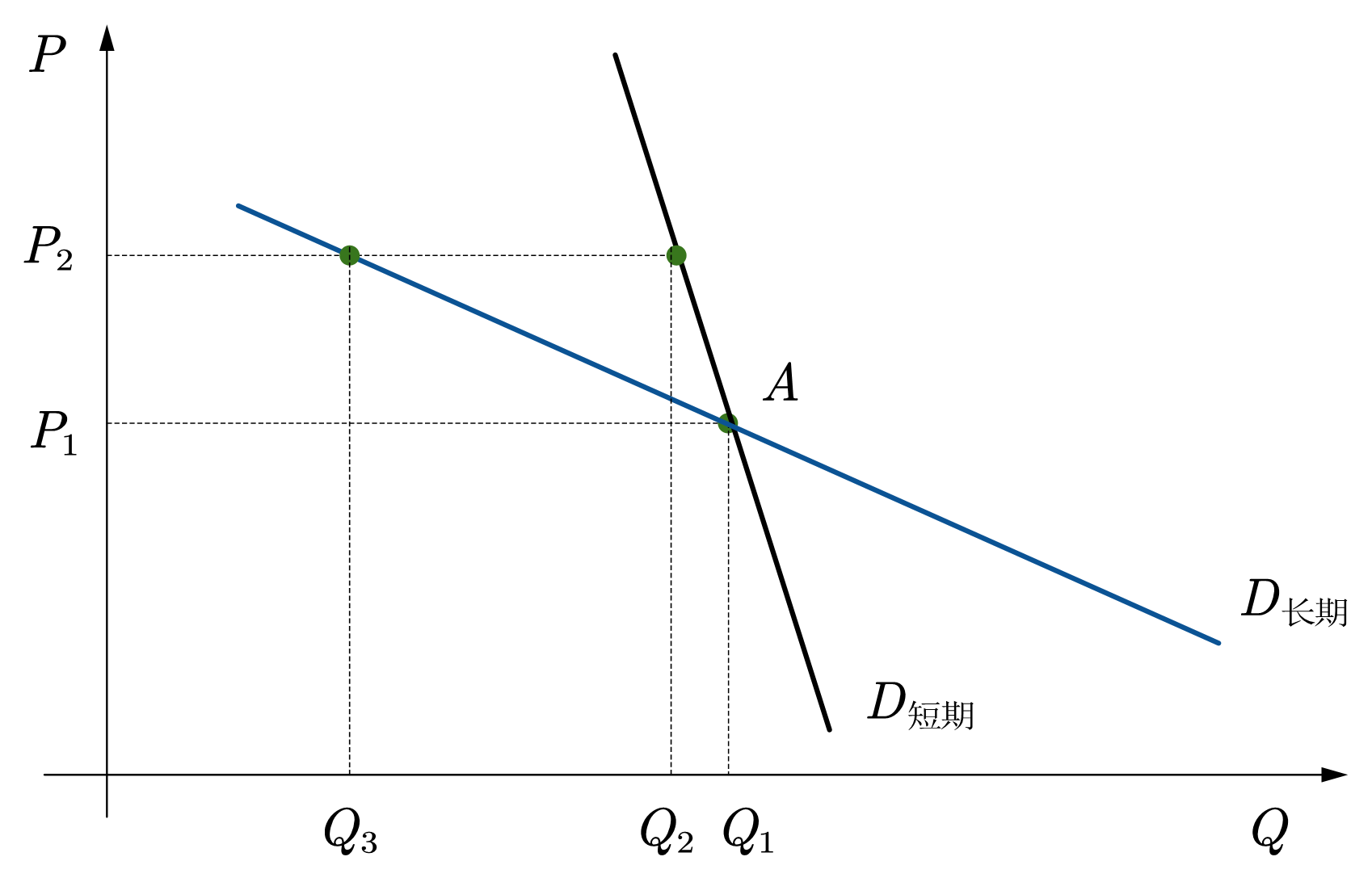
../../_images/ds-1-demand-long-short-run.png

Fig. 27 在点A处，需求曲线越平坦，越富有需求的价格弹性。#

幂函数和线性函数需求形式

需求函数为\(Q^d = aP^b\)时，\(b<0\), 需求的价格弹性为\(b\)。

证明：

  • \(Q^d = aP^b \Rightarrow ln(Q^d) = ln(a) + bln(P)\)

  • \(E_d = \frac{d\ln Q^d}{d\ln P} = b\)

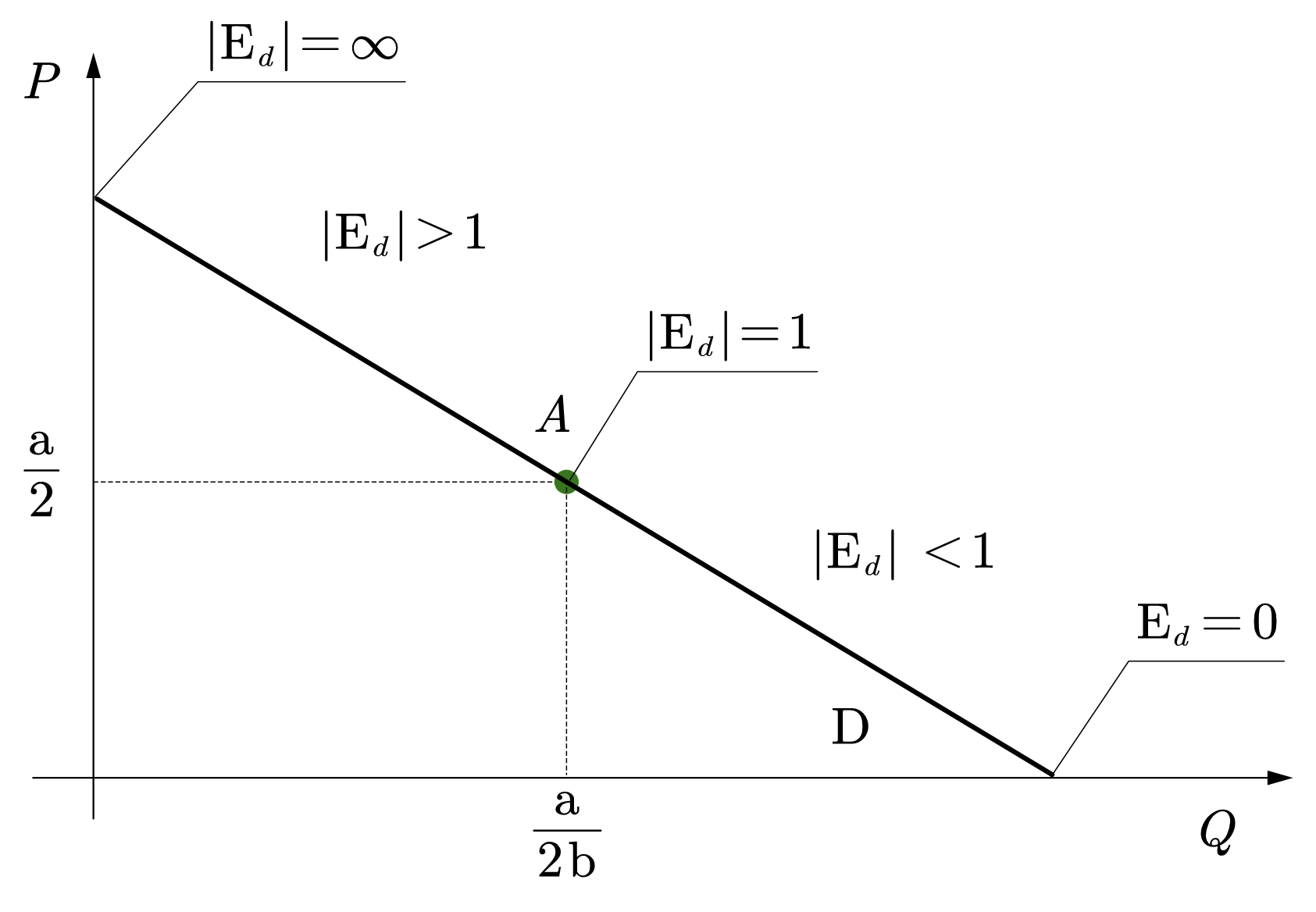
需求函数为\(Q^d = a-bP\)时，\(a,b>0\), 价格弹性点点不同，其特征为：在曲线的中点处，价格弹性为单位弹性；当价格小于中点价格时，价格弹性为缺乏弹性；当价格大于中点价格时，价格弹性为富有弹性。

证明1：

  • 在中点处，\(Q^d = \frac{a}{2}\), \(P = \frac{a}{2b}\)，根据式(2)，可得 \(|E_d| = 1\)

  • 在曲线的上半段：\(Q^d < \frac{a}{2}, \ P > \frac{a}{2b}\), 可得\(|E_d|> 1\)。 在纵轴截距处，\(P = \frac{a}{b}, Q^d = 0 \Rightarrow |E_d| = \infty\)

  • 在曲线的下半段：\(Q^d > \frac{a}{2}, \ P < \frac{a}{2b}\), 可得\(|E_d|\in [0,1)\)。在横轴截距处，\(P = 0, Q^d = a \Rightarrow E_d = 0\)

证明2：线性需求下，每一点的弹性绝对值等于需求曲线上被该点分成的两段线段的长度之比。

如图28 (b) 所示，我们可以将A点的弹性表示为：

\[ E_d = \frac{dQ^d/dP}{P/Q} = -\frac{BO}{CO}\frac{AM}{AN} = -\frac{BO}{AN}\frac{AM}{CO} \]

\(\because \quad AN = MO, AM=NO\)

\(\therefore E_d = -\frac{BO}{MO}\frac{NO}{CO} \quad (p.1)\)

基于相似三角形的性质：

\[ \frac{BO}{MO} = \frac{BC}{AC} \quad \frac{NO}{CO} = \frac{AB}{BC} \]

带入(p.1)中可得，

\[ E_d = - \frac{BC}{AC}\frac{AB}{BC} = -\frac{AB}{AC} \]

  • 在中点处，\(AB = AC\), \(E_d = -1\)

  • 在曲线的上半段：\(AB>AC\), \(|E_d| > 1\)。

  • 在曲线的下半段：\(AB<AC\), 可得\(|E_d|\in [0,1)\)。

(a) (a)
(b) (b)

Fig. 28 线性需求曲线：在中点处，需求的价格弹性为单位弹性，上半部分为富有弹性，下半部分为缺乏弹性。#

影响需求的价格弹性大小的因素#

一方面，替代品的可获取性会对价格弹性产生影响。当商品价格上涨时，如果消费者能够更容易地选择其它可替代的商品，商品就会更富有价格弹性；反之，如果替代品较少，消费者用其它商品替代消费的能力较弱，那么商品就会缺乏价格弹性。

首先，通常而言，市场界定越小的商品，替代品会越多，该商品越富有价格弹性，如哈伦裤和衣服，电动车和汽车，以及橙汁和饮品，这三组商品都是前者的市场范围小于后者（是后者的一个子类）。以哈伦裤和衣服为例，如果哈伦裤价格上涨，消费者可以选择购买其它类型的裤子作为替代品，而当衣服价格上升时，可替代商品却较少，因此哈伦裤的价格弹性的绝对值必然大于后者。

其次，相较于必需品，奢侈品有更多的替代品，因此更富有价格弹性，如豪华游轮和胰岛素。奢侈品对收入变化敏感，而必需品对收入变化不敏感，是我们总要购买的商品。总要购买说明缺乏替代品，如胰岛素可以认为是没有替代品的（但不同品牌的胰岛素会具有替代性）。

此外，时间跨度越长，消费者的选择余地会越大，可替代商品数量也就越多，这一点在需求定律部分中的需求曲线与时间的关系也有提到。

另一方面，支出在消费者预算中占比较大的商品通常更富有价格弹性，如汽车和白糖。支出占比低的商品，比如白糖，即使价格波动较大，也不会对其占比产生太大影响，自然消费者对其价格变化也就不敏感了。

需求的价格弹性对销售收入的影响#

销售收入等于商品的价格乘以销售量（\(R=P*Q\)）。假设销售者现在决定对某种商品提价，这会使他们从单位商品中获得的收入上升，但是受需求定律的约束，商品出售的数量也会相应下降，这一升一降最终会如何影响总收入的变化呢？变量之间的影响可以用导数表示，因此，价格对收入的影响可以转换为判断收入对价格求导的数值特征（正值或负值），具体推导如下，

\[\begin{split} \begin{array}{lll}\frac{dR}{dP}&=&Q+P\frac{dQ}{dP}\\ &=&Q(1+\frac{P}{Q}\frac{dQ}{dP})\\ &=&Q(1-|E_d|) \end{array} \end{split}\]

上式表明，价格对收入的影响取决于需求的价格弹性：

  • 当商品富有价格弹性时（\(|E_d|>1\)），价格与销售收入反向变化——价格上升，收入下降；价格下降，收入上升。

  • 当商品缺乏价格弹性时（\(|E_d|<1\)）,价格与销售收入同向变化。

  • 当商品具有单位价格弹性时（ \(|E_d|=1\) ），价格变化不影响销售收入。

该结论可以为商品定价提供思路，当商品缺乏弹性时，提价会增加销售收入。如巴菲特喜爱的喜诗糖果，就具有年年提价的能力。而当商品富有弹性时，提价会降低销售收入和商品的市场份额。考虑房地产商对主力户型（70-90平米）和大户型（150-200平米）的定价，假设市场上的均价为2-3万一平米，如果你是房地产商会如何定价呢？若不考虑其它因素，通常购买主力户型属于刚需，缺乏弹性，而大户型大多是改善性需求，较富有弹性，且面积大整体支出也较多，因此，前者的定价可以考虑在价格区间的上部——提价以增加收入，后者的定价在区间下部——降价以增加收入。需要注意的是，弹性会随着价格的变化而改变，因此提价不能是任意幅度的提价，若提价过高时，商品的需求可能会转为富有价格弹性。

这里的分析结果同样适用于价格对消费者支出的影响，这是因为销售者的销售收入等于消费者的支出，所以收入和支出是一个问题的两面，如在GDP核算中，有收入法和支出法两种方法。例如，分析胰岛素价格上升对消费者支出的影响，我们可以通过对胰岛素缺乏价格弹性的判断，得出消费者支出会上升的结论。

对于弹性与收入的关系，我们还可以推出一个结论：如果卖方希望最大化收入，或者在成本接近于0时最大化利润，那么应选择在单位弹性处定价。

需求的交叉价格弹性#

需求的交叉价格弹性（简称为交叉价格弹性）衡量的是一种商品的价格变化对其它商品需求量的影响:

\[ 𝐸^d_{12}= \frac{𝑑𝑄_1^𝑑}{dP_2}*\frac{P_2}{𝑄_1^𝑑} = \frac{𝑑 \ln 𝑄_1^𝑑}{𝑑 \ln P_2} \]

  • 如果两商品为替代品，那么它们的交叉价格弹性为正，这是因为当一种商品的价格增加时，另一种商品的需求会增加，从而导致其需求量的上升。

  • 如果两商品为互补品，那么它们的交叉价格弹性为负，这是因为当一种商品的价格增加时，另一种商品的需求会降低，从而导致其需求量的减少。

收入弹性#

收入弹性衡量消费者的收入对商品需求量的影响:

\[𝐸_𝑀= \frac{𝑑𝑄^𝑑}{dM}∗\frac{𝑀}{𝑄^𝑑}=\frac{𝑑 \ln 𝑄^𝑑}{𝑑 \ln 𝑀}\]

如果收入增加会使消费者对某种商品的需求增加，进而带来需求量的上升，即收入弹性为非负（\(𝐸_𝑀\geq0\)），那么，我们称这种商品为正常商品（normal goods），比如，收入增加，我们可能会增加对外出就餐或高档次商品的需求。反之，如果收入增加会使消费者对某种商品的需求减少，进而带来需求量的下降，即收入弹性为负（\(𝐸_𝑀<0\)），那么，我们称这种商品为贫穷商品(inferior goods)，比如，收入增加，我们可能会减少对方便面或路边小吃的消费。

将\(𝐸_𝑀<0\)的商品称为贫穷商品1，而非直译为劣等品（大部分书中使用称谓）是因为随收入增加而减少消费的商品不一定是劣质的。

在正常商品中，我们还可以进一步划分：若商品的收入弹性在0和1之间，称之为必需品，其需求量对收入的变化不敏感；若收入弹性大于1，称为奢侈品。

供给的价格弹性#

供给的价格弹性衡量的是商品的价格变化对卖方供给量的影响，即在同一条供给曲线上的价量关系:

\[ E_s = \frac{𝒅𝑸^𝒔}{𝒅𝑷}∗\frac{𝑷}{𝑸^𝒔} = \frac{𝒅 \ln 𝑸^𝒔}{𝒅 \ln 𝑷} \]

因为供给曲线向右上方倾斜，所以供给弹性为正。影响供给的价格弹性大小的因素主要与生产调整的灵活程度有关，调整越灵活，供给的价格弹性越大。如，小作坊通常比规章繁琐的大企业更灵活调整生产，火电站在短时间内比核电站发电的灵活度更高。再如，对于生产，通常都会有产能限制，如发电机组的装机容量，当产量接近装机容量时，将难以继续提升，因此其供给曲线会变的陡峭，供给弹性接近于完全无弹性。此外，时间跨度也会影响生产调整的灵活程度。

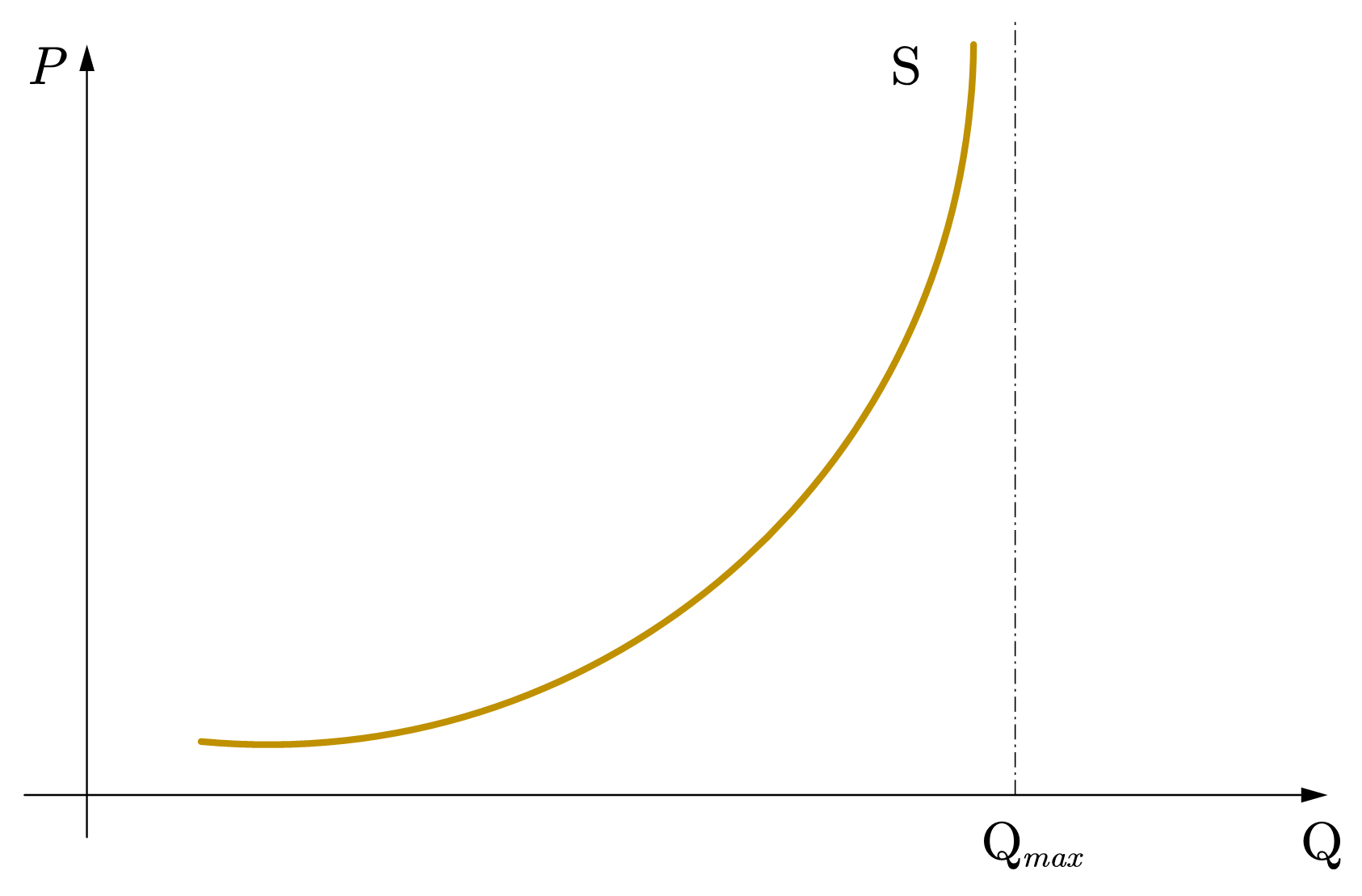
../../_images/ds-4-elas-supply-capacity.png

Fig. 29 \(Q_{max}\)为企业的最大产能，当产量接近最大产能时，越缺乏供给的价格弹性。#

同样，市场界定也会影响供给的价格弹性，市场界定越大，供给的价格弹性越小；市场界定越小，供给的价格弹性越大。比如，通常我们认为土地供给的价格弹性接近于完全无弹性，但是，如果细分土地用途，如商业用地，工业用地，住宅用地等，那么，在不同用途下的土地供给价格弹性会有所增加。

供给的交叉价格弹性#

供给的交叉价格弹性衡量的是一种商品的价格变化对其它商品供给量的影响:

\[E^s_{12} = \frac{dQ_1^s/Q_1^s}{dP_2/P_2}=\frac{d\ln Q_1^s}{d\ln P_2}\]

如果商品1和2的生产会使用相同的资源，并且生产是相互排斥的，即将资源用于生产商品1就不能生产商品2，反之亦然，那么，我们称这两种商品为生产性替代品（Substitute-in-production），其所对应的供给的交叉价格弹性为负（\(E^s_{12}<0\)）。其中的逻辑链条为：假设商品2的价格上升，商品2的供给量增加，使用的资源也会相应增加，又因为商品1和2为生产性替代品，所以商品1的供给会减少，从而带来其供给量的下降。比如，汽车厂商的车型平台既可以用于生产轿车，也可以生产SUV车型。当两种商品为生产性替代品时，企业会倾向于生产畅销或毛利率高的商品。

如果商品1和2可以由相同的资源共同产出，即商品1的产量增加会伴随着商品2的产量增加，那么，我们称这两种商品为生产性互补品（Complement-in-production），其所对应的供给的交叉价格弹性为正（\(E^s_{12}>0\)）。其中的逻辑链条为：假设商品2的价格上升，商品2的供给量增加，使用的资源也会相应增加，又因为商品1和2为生产性互补品，所以商品1的供给会增加，从而带来其供给量的上升。比如，小麦胚芽是小麦面粉加工的副产物，所以小麦胚芽和面粉是生产性互补品。

考考你

假设商品1的需求函数为：

\[𝑸_𝟏^𝒅=𝒂𝑴^𝑺 𝑷_𝟏^{−𝑵}𝑷_𝟐^{−𝑲}\]

其中，\(M\)是收入，\(a,S,N,K>0\) 为参数。请计算商品1需求的价格弹性、交叉价格弹性和收入弹性。

答：我们可以对需求函数两边取对数（\(\ln\)），并应用弹性公式计算相应的弹性：

\[\begin{split}\begin{align*} \ln 𝑸_𝟏^𝒅 & = \ln 𝒂 + S\ln 𝑴 -N \ln 𝑷_𝟏 - K \ln𝑷_𝟐\\ & E_d = \frac{\partial \ln Q_1^d}{\partial \ln P_1} = -N\\ & E_{12} = \frac{\partial \ln Q_1^d}{\partial \ln P_2} = -K\\ & E_{M} = \frac{\partial \ln Q_1^d}{\partial \ln M} = S \end{align*}\end{split}\]

注意

弹性严格来说是一个后验的概念，是根据历史（过去的数据）得来的，本质是归纳法，因此归纳法的问题在此也适用。如果局限条件变化或不稳定，那么，由历史数据得来的弹性不一定有助于现在的决策。

1

参见张五常《科学说需求》