附录A:寡头市场#
寡头市场上的企业数量较少,这意味着市场上只有少数几家企业控制大部分市场份额。这些企业提供的商品可以是同质的,也可以是异质的。当市场上只有两家企业时,这种情况被称为双寡头市场(Duopoly)。典型的寡头市场实例包括中国的石油市场(中国石油和中国石化)、电信市场(中国移动、中国联通和中国电信),以及动力电池市场(比亚迪和宁德时代)等。
在寡头市场中,企业的决策会影响到竞争对手,并反过来受到竞争对手决策的影响。因此,企业不仅要考虑自身的成本和收益,还需要将其他企业的行为或选择纳入考量,即进行策略性思考。例如,在制定价格或产量决策时,企业会考虑对手可能的反应。一家企业可能会考虑降价以吸引更多客户,但如果预计竞争对手也会随之降价,则这种策略可能会导致价格战,损害所有参与者的利益。同样,增加产量以扩大市场份额也可能引发竞争对手的反击,导致市场供应过剩和价格下跌。为了更好地理解和推断寡头市场中的企业行为,我们将运用博弈论的知识来分析这些策略互动,并找到它们的最优决策。
为了简化分析,我们都假设市场上的商品是同质的。如果企业之间没有合作或串谋,寡头市场可以划分为数量竞争模型和价格竞争模型。在数量竞争模型中,企业的决策变量为产量,商品价格由市场决定;在价格竞争模型中,企业的决策变量为商品的价格,产量由市场决定。
依据企业的行动顺序,数量竞争模型又可以划分为古诺模型(Cournot Model)和斯塔克伯格模型(Stackelberg Model)。在古诺模型中,企业在做产量决策时,并不知道其他企业的选择;在斯塔克伯格模型中,企业决策有先后顺序,我们将先决策的企业称为领导者,后决策的企业称为跟随者。跟随者会看到领导者的产量决策后再做决策。
同样,在价格竞争模型中,也可以依据企业的行动顺序划分为伯兰特模型(Bertrand Model)和价格领导者模型。前者是企业在不知道其他企业选择时,决定自己所售商品的价格;后者是领导者决定商品的市场价格,跟随者是该价格的接受者。
古诺模型和伯兰特模型属于博弈论中的同时行动博弈;斯塔克伯格模型和价格领导者模型则属于博弈论中的序贯博弈。
check add examples!
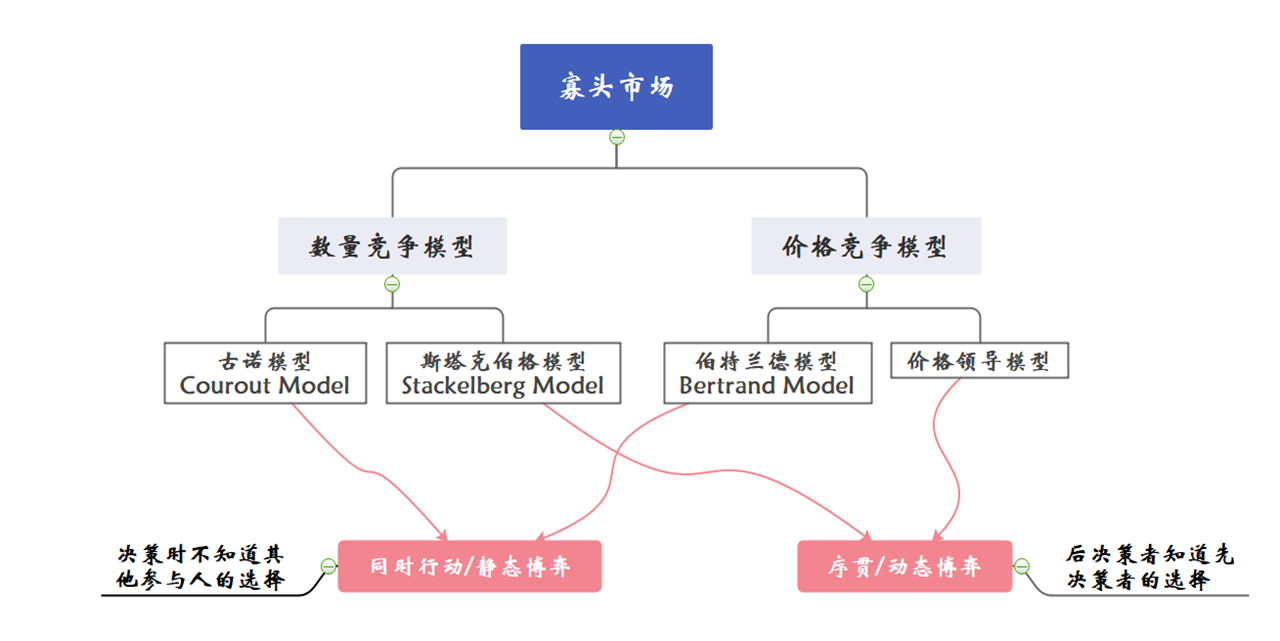
Fig. 103 寡头市场模型#
一些寡头市场
空调市场:格力和美的
定制家具市场:欧派和索菲亚
监控市场:海康威视和大华
游戏市场:腾讯和网易
摄像头模组市场:欧菲科技和舜宇光学
玻璃视窗防护屏市场:蓝思科技和伯恩光学
增值税税控系统市场:航天信息和百望金赋
手机市场:苹果,华为,ov和小米
如果企业之间存在合作,像垄断者一样进行决策,则称为卡特尔模型(Cartel Model)。例如,OPEC(石油输出国组织)就是一个著名的卡特尔。与垄断模型不同的是,卡特尔组织存在脆弱性,其成员有动力偏离既定的产量决策。
在不同的模型设定下,寡头市场会产生不同的均衡结果。因此,我们无法得到唯一确定的价格和产出均衡,也就无法对寡头市场做出确定性的推断。
动力电池市场: 比亚迪 v.s. 宁德时代
在2023年的全球动力电池市场版图上,比亚迪与宁德时代作为双寡头的影响力进一步凸显,两者在全球市场的占有率合力突破半数以上,有力地驱动了中国乃至全球新能源汽车产业链的迅猛发展。这一年标志着双方竞争步入全新阶段,在技术创新、产能扩张和市场份额争夺等方面展开了更为激烈的较量。
宁德时代作为全球最大的动力电池制造商,在技术层面持续加大研发投入,力求保持其在电池能量密度、循环寿命和成本控制等方面的竞争优势。尽管面对市场份额的小幅下滑,但宁德时代依托其规模化生产优势和广泛的客户网络,依然能够确保在全球电动汽车电池供应体系中的主导地位。此外,宁德时代还积极布局固态电池等下一代电池技术的研发,以期在未来的技术革命中抢占先机。
与此同时,比亚迪凭借刀片电池这一独门绝技,实现了市场份额的显著提升,并成功超越LG能源成为全球第二的动力电池供应商。比亚迪的刀片电池技术通过创新的结构设计,有效解决了传统磷酸铁锂电池能量密度较低的问题,同时强化了电池的安全性能,从而在市场上赢得了良好的口碑与订单。不仅如此,比亚迪还拥有从上游原材料到下游整车制造的完整产业链,这使其在应对国际市场竞争以及应对如美国《通胀削减法案》等政策变动时具备更强的抗风险能力。
两家巨头的竞争策略各有侧重:宁德时代注重全球化布局与高端客户的绑定合作;而比亚迪则依靠全产业链整合及独特的技术路线,实现垂直一体化的优势。双方都在新能源汽车发展的关键赛道上加速奔跑,不断推动着整个行业向更高效、更安全、更环保的方向发展。随着市场环境的变化和技术进步的步伐加快,比亚迪与宁德时代的双雄争霸战将进一步塑造未来全球动力电池市场的格局。
【例子:超市,低价退货policy】
数量竞争模型#
古诺模型 (The Cournort Model)#
基本设定#
市场状况:市场上有两家企业,生产同质商品。
成本结构:两家企业的成本结构相同,且都知道对方的成本函数。假设成本函数为 \(C(q)\)。
市场需求:市场的反需求函数为 \(P = P(Q)\), 其中,\(Q = q_1 + q_2\),\(q_1\)和\(q_2\)分别为两企业的产量。
决策过程:两企业分别选择各自的产量以最大化利润。因为两企业的产量共同影响商品的市场价格,所以企业的利润不仅受自身选择的影响,还会受到其他企业的决策影响,即企业的决策是相互影响的。利润最大化问题可表示为:
企业1:\(\max_{q_1} P(q_1+q_2)q_1 - C(q_1)\)
企业2:\(\max_{q_2} P(q_1+q_2)q_1 - C(q_2)\)
以企业1为例,如果我们按照常规的最优化问题解决思路,即令一阶条件等于0(边际收益等于边际成本),是无法求解的。原因在于企业1的产量决策会受到企业2的影响——企业2的决策直接影响企业1的边际收益,而它们之间的关系(\(\frac{dq_2}{dq_1}\))我们是不清楚的。
为了解决企业之间相互影响的最优化问题,我们将采用纳什均衡的概念来定义企业的最优决策。相应地,古诺模型的解被称为古诺纳什均衡。
纳什均衡
纳什均衡是这样一种参与人的策略组合(对于古诺模型,是两企业的产量组合),在该策略组合上,任何参与人单独改变策略都不会得到额外的好处。换句话说,如果在一个策略组合上,当所有其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡。
古诺纳什均衡#
纳什均衡的核心在于企业的选择相互为最佳对应。在古诺模型中,最佳对应意味着企业的选择是在给定其他企业选择的情况下做出的最优决策。这意味着我们在计算一阶条件时,可以将其他企业的产量视为外生变量,并据此表示出企业的最优产量;相互指的是企业1的决策是对企业2的最佳对应,反之亦然。相应的分析步骤可以总结为:
第一步:用其他企业的产量(\(q_j\))表示企业的最优决策(\(q_i\)),称为最佳反应函数。
企业\(i\)的一阶条件为(给定\(q_j\)):
\[\frac{dP}{dQ}q_i + P(Q) - MC(q_i) = 0\]可以计算得到企业\(i\)的最佳反应函数:
\[q_i = f_i (q_j),i\neq j\]第二步:联立两企业的最佳反应函数,求解企业的最优决量。
\[\begin{split} \begin{align*} & \begin{cases} q_1 &=& f_1(q_2)\\ q_2 &=& f_2(q_1) \end{cases}\\ & \Rightarrow \quad q_1^*\ ,\ q_2^* \end{align*} \end{split}\]第三步,由两企业的最优产量,计算商品的市场价格。
- \[ P^* = P(q_1^*, q_2^*) \]
基于两企业的最佳反应函数,我们画出了他们的最佳反应曲线,如\numref{`图<>’}所示。点A表明给定企业2的产量是\(q_2'\),企业1将产量定为\(f_1(q_2')\)可以最大化利润。两曲线的交点为古诺纳什均衡。
在\numref{`图<>’}中,我们画出了两企业的等利润线,对企业1而言,给定其产量,企业2的产量越低,商品的市场价格越高,对应的等利润线代表的利润越高。同理,企业2的等利润线也是随着企业1产量的降低而升高。假设企业2的产量为\(q_2\),A点所对应的产量,\(q_1^A\),为企业1的最佳对应,这是因为A点所对应的等利润线与过\(y= q_2\)的水平线相切,这是企业1所能获得的最大利润——在其它产量下,企业1的利润会降低。这表明,企业1的最佳反应曲线即为是等利润线最高点的连线。
check 【加图】
计算古诺纳什均衡
我们看一个古诺模型的例子,假设市场的反需求函数为:\(P=a-bQ\),\(a,b>0\),两企业的成本函数为\(C = cq\), \(a>c\)。请计算古诺纳什均衡。
第一步:计算两企业的最佳反应函数。
给定企业\(j\)的产出,企业\(i\)的利润最大化问题为: $\( \max_{q_i} (a-b(q_i+q_j))q_i - cq_i \)$
由一阶条件(F.O.C),即\(MR = MC\),可得企业\(i\)的最佳反应函数,
第二步:联立两企业的最佳反应函数,可以求得最优产量。或者,因为两企业是同质的,所以它们的最优产量相等,将这一条件代入最佳反应函数中,也可以求解出最优产量。
第三步,将两企业的最优产量带入反需求函数,计算商品的市场价格。
古诺纳什均衡为:\((\frac{a-c}{3b}, \frac{a-c}{3b})\), 商品市场价格为:\(\frac{a+2c}{3}\)。
与受价和垄断市场进行对比
基于此题目的设定,我们可以与受价市场和垄断市场进行对比。
若市场为受价市场,企业是价格的接受者,均衡时,商品的市场价格等于边际成本,\(P^c = c\),由此可以得到,市场的总产量为 \(Q^c = \frac{a-c}{b}\),高于古诺市场的总产量。
若市场为垄断市场,则 \(P^M = \frac{a+c}{2}\),\(Q^M = \frac{a-c}{2b}\),低于古诺市场的总产量。
由此可得,古诺市场的总产量高于垄断市场,低于受价市场;相应的,古诺市场的商品价格低于垄断市场,高于受价市场。
check 需要注意这里的计算顺序
企业数量趋向无穷的古诺模型
证明:当市场中的企业数量\(n\)趋于\(+\infty\)时,古诺市场中的商品总产量和价格趋于受价市场均衡。 (市场反需求函数和企业的成本函数与上题相同)
对于任一厂商\(i\)的利润最大化问题 (给定所有其它企业的产量):
F.O.C. \(\quad a-2bq_i-b\sum_{j\neq i} q_{j} = c\)
\(\Rightarrow \quad q_i=(a-b\sum_{j\neq i} q_{j}-c)/2b\)
因为所有企业是同质的,所以均衡时,所有企业的产量相等:\(q_i=q, \ \forall i\) ,可得,
市场总产量为:
当n趋向于无穷时(使用洛必塔法则),
Q.E.D.
斯塔克伯格模型 (Stackelberg Model)#
斯塔克伯格模型与古诺模型的区别在于两企业的行动顺序有先后,先行动的企业通常具有有一定的市场优势,能够先行做出产量决策,被称为“领导者”;后行动的企业被称为“追随者”, 其最优决策取决于领导者的决策。具体的决策顺序为:
领导者先做出产量决策;
跟随者在看到领导者的决策后,再决定自身的产量。
如果跟随者选择了在给定领导者行动下的非最优行动,这不仅会影响跟随者的收益,也会影响领导者的收益。因此,领导者的最优决策是建立在假设跟随者能够看到领导者的行动,并且会根据领导者的行动来最大化自身收益的基础上。换言之,当决策有先后顺序时,先选择的一方会将后选择一方的决策纳入考量,这说明我们需要倒着进行分析。假设企业1为领导者,企业2为跟随者。基本的分析步骤如下:
第一步:给定企业1的产出,求解企业2的最佳反应函数。
第二步:将企业2的最佳反应函数带入企业1的目标函数中,求解企业1的最优产量。
第三步:将企业1的最优产量带入企业2的最佳反应函数中,求解企业2的最优产量。
第四步:将两企业的最优产量代入市场的反需求函数,得出商品的市场价格。
以上倒着分析问题的思路称为逆向归纳法。
如\numref{图%s
因为企业1的利润会随着其等利润线的向下移动而增加,所以当等利润线与AB相切时,其产量,\(q_1^*\),为企业1的最优选择。和古诺模型相比,企业1的产量和利润都得到了提高,可以认为企业1具有先行者优势。直觉上,因为古诺模型的解是企业1的可选产量,所以,其利润必然不会低于古诺模型中利润。
【举个例子呢?check】
项目管理 check
这些文章探讨了斯塔克伯格模型在项目管理和相关领域的应用:
Title: “Stackelberg Games for Project Management: A Strategic Approach”
Title: “Applying Stackelberg Games to Optimize Resource Allocation in Project Management”
Title: “Strategic Decision Making in Project Scheduling Using Stackelberg Games”
Title: “Stackelberg Games for Managing Risks in Large-Scale Projects”
Link: Risk Analysis
Title: “Optimizing Project Portfolio Selection Using Stackelberg Games”
计算斯塔克伯格模型中两企业的最优产量
在古诺模型的练习中,令企业业1为领导者,企业2为跟随者,求解两企业的最优产量。
第一步:使用逆向归纳法,先给定\(q_1\),求解企业2的最佳反应函数: $$
q_2^* = \frac{a-c-bq_1^*}{2b} = \frac{a-c}{4b} $$
价格竞争模型#
伯兰特模型 (Bertrand Model)#
与古诺模型一样,在伯兰特模型中,我们假设市场上有两个同质厂商,生产同质商品,且双方都知道对方的成本结构,成本函数为\(C= cq\)。与古诺模型的不同之处在于,两企业分别选择商品的定价以最大化自身的利润。
因为商品是同质的,所以定价较低的企业可以占据整个市场;如果两企业的定价相同,则假设平分市场。假设市场的需求函数为 \(Q^d = q(P)\),企业 \(i\)(\(i\neq j, i,j\in\{1,2\}\))的需求函数可以表示为,
企业 \(i\) 的利润最大化问题为: $\( \max_{p_i} \ p_if_i(p_i,p_j)-cq_i \)$
因为企业的需求函数为分段函数,我们无法直接对目标函数求一阶条件来计算最佳反应函数。这时,利用纳什均衡的特征可以帮助我们分析两企业的最优定价。纳什均衡意味着企业的选择相互为最佳对应,这意味着给定其他企业的最优选择,企业是不会偏离它的最优决策的。不偏离说明改变选择不会带来利润的严格增加。
接下来,我们会穷尽两企业不同的定价组合,通过思考是否会有企业会选择偏离来判断它们是否能够构成纳什均衡。
组合1: \(\{(p_i,p_j)\ |\ c<p_i<p_j\}\)
企业 \(i\) 拥有全部的市场份额,利润为正,而企业\(j\)的利润为0。这时,给定\(p_i\),企业\(j\)可以通过降价增加利润,比如将价格定为与\(p_i\)相等 — 占有一半的市场份额,或略低于\(p_i\)(仍大于\(c\))— 占有全部市场。因此,企业\(j\)有动力偏离。
组合1不能构成纳什均衡。
组合2:\(\{(p_i,p_j)\ |\ c<p_i=p_j\}\)
企业 \(i\) 和 \(j\) 平分市场,且利润为正。这时,企业 \(i\) 和 \(j\) 都有动力降价,比如,给定 \(p_i\),企业 \(j\) 可以通过降价占据全部市场使利润增加。我们可以找到一个可行的降价幅度\(\epsilon\), 使企业 \(j\) 降价后利润增加,即
\[ p_j-\epsilon > c \]且 $\( \frac{1}{2}q(p_j)(p_j-c) < q(p_j-\epsilon)(p_j-\epsilon-c) \)$
因此,企业\(i\)和\(j\)都有动力偏离。
组合2不能构成纳什均衡。
组合3: \(\{(p_i,p_j)\ | \ c=p_i<p_j\}\)
企业 \(i\) 拥有全部的市场份额,利润为0,企业 \(j\) 没有生产,利润也为0。这时,给定 \(p_j\),企业 \(i\) 有动力提价,比如,令 \(p_i' = p_i+\epsilon < p_j\),企业 \(i\) 仍拥有全部的市场份额,利润变为正。因此,企业\(i\)有动力偏离。
组合3不能构成纳什均衡。
组合4: \(\{(p_i,p_j)\ | \ p_i<p_j<c\}\) 或 \(\{(p_i,p_j)\ | \ p_i<p_j=c\}\)
企业 \(i\) 拥有全部的市场份额,但利润为负。显然,给定 \(p_j\),企业 \(i\) 有动力提价。
组合4不能构成纳什均衡。
组合5: \(\{(p_i,p_j)\ | \ p_i=p_j<c\}\)
企业 \(i\) 和 \(j\) 平分市场,但利润为负。显然,给定对方的选择,两企业都有动力提价。
组合5不能构成纳什均衡。
基于以上分析,可以得出结论:当两企业价格不相等时,以及价格相等但不等于边际成本时,都不能构成纳什均衡。
组合6: \(\{(p_i,p_j)\ | \ p_i=p_j = c\}\)
企业 \(i\) 和 \(j\) 平分市场,且利润都为0。给定 \(p_i\),企业 \(j\) 不会偏离,因为提价会丧失市场,利润仍为0,降价虽可占据市场但利润为负。同理,企业\(i\)也不会偏离。
组合6是纳什均衡。
综上所述,在伯兰特模型中,两企业的最优定价等于 \(c\),即商品的价格等于边际成本,企业没有垄断势力,与受价市场相同。这一结论被称为「伯兰特悖论」。之所以称之为悖论,是因为它挑战了将企业数量作为市场结构划分标准的传统观点。在现实中,我们不能仅凭企业数量来推断它们的市场势力,不要忘记垄断势力是由进入门槛决定的,即使市场只有一家企业,也可能是一个受价市场。
为什么伯兰特模型的结果会和受价市场一样呢?#
伯兰特模型有一个暗含的约束条件:两企业都没有产能限制,可以满足全部的市场需求。这意味着只要有一方的定价高于边际成本,\(c\),另一方便可以略微降价并迅速扩产占据市场,直至商品的市场价格等于边际成本。因此,在伯兰特模型中,企业没有提价能力,这相当于市场没有门槛,是一个受价市场而非觅价市场。这也说明:
对于受价企业而言,潜在的竞争者实际上不需要很多。
单纯的价格战没有意义,如果不能建立门槛,那么总会有潜在的竞争者进入市场与之争夺利益。
如果调整模型设定,增加与门槛相关的假设,那么企业便会具有垄断势力。例如:
增加产能限制 —— 单一企业不能满足市场需求;
引入产品差异 —— Hotelling 模型说明具有位置差异的企业可以具有市场势力;
或者引入成本差异 —— 边际成本低的企业会具有垄断势力。
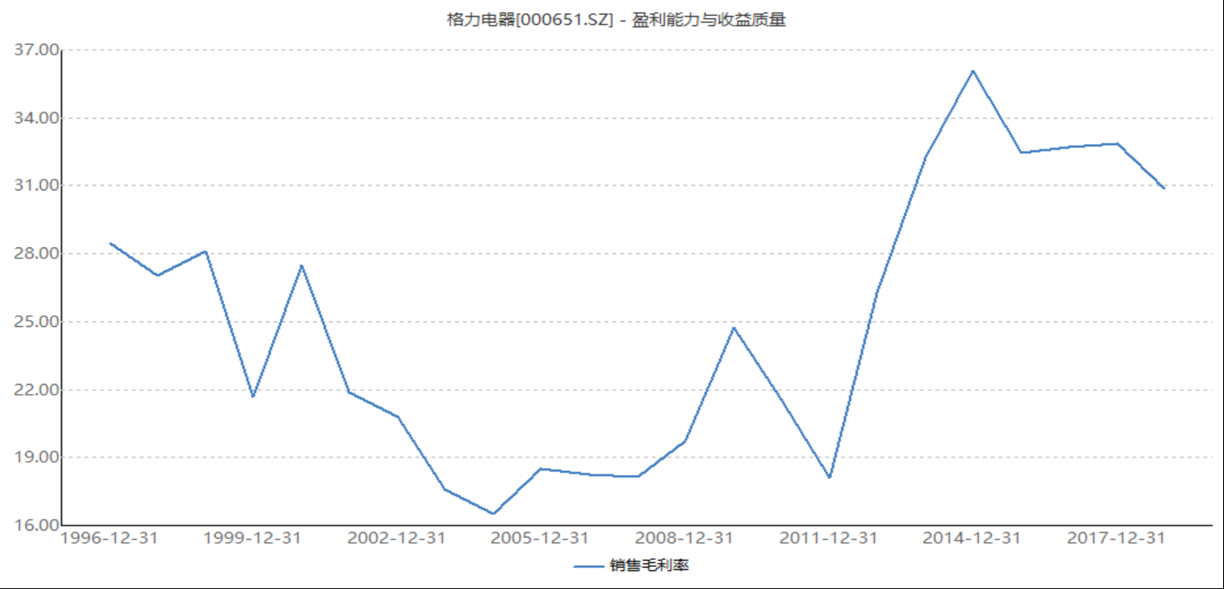
格力电器的价格战
•空调类公司
•2000-2006****年: 竞争非常激烈,规模壁垒不明显
•空调、冰箱、洗衣机**—**技术壁垒不高,门槛低,利润高,吸引很多人进入,
•差的竞争格局
•**2006- :****格力,美的寡头垄断。**龙头企业在规模、渠道、品牌等方面的优势扩大,不断高筑护城河,使得新进入者成本越来越高,行业格局从野蛮生长的无序竞争变为有门槛的有序竞争。
价格领导者模型#
与斯塔克伯格模型类似,价格领导者模型假设市场中的两企业分别为领导者(企业1)和追随者(企业2),先后做出决策:
企业1首先确定商品定价。
企业2将企业1的定价视为外生给定,在此基础上决定自己的最优产量。企业2类似于受价厂商,是企业1定价的接受者。
因为企业的行动有先后顺序,所以我们使用逆向归纳法进行分析,分析步骤为:
第一步:给定企业1的定价,求解企业2的最佳反应函数。
因为企业2是价格的接受者,所以企业2产出的最优条件满足:\(p_1 = MC_2(q_2)\),可得企业2的最佳反应函数为: $\( q_2 = f_2(p_1) \)$
第二步:给定企业2的最佳反应函数,企业1可以计算它所面对的剩余市场需求(\( = Q(p_1) - f_2(p_1)\)),其利润最大化问题为给定剩余市场需求的垄断企业的单一定价问题。:
\[ \max_{p_1} p_1*(Q(p_1)- f_2(p_1)) - c_1(Q(p_1)- f_2(p_1)) \]通过求解一阶条件,可以得到企业1的最优定价。
第三步:将企业1的最优定价带入企业2的最佳反应函数中,求解企业2的最优产量。
第四步:计算企业1的最优产量。
【三星液晶屏定价的例子 check 】
芯片行业
芯片行业主要包括三个步骤:设计、制造(代工)、封装和检测。其中,制造环节尤为关键,涉及高度专业的技术和巨额的投资。比如,建造一家芯片代工厂可能需要投入数百亿的资金,同时还需要掌握多项相关技术。因此,芯片代工厂的门槛非常高,而且它们还面临着巨大的能源消耗问题,尤其是电力和水资源的消耗量极大。
目前全球仅有少数几家企业能够进行芯片代工,其中台积电表现最为突出,占据了全球市场约40%至50%的份额。中国大陆的中芯国际也在这一领域有所发展,尽管市场份额相对较小,大约在10%左右。这些企业在制造环节的毛利率各不相同,台积电的毛利率约为40%,而其他一些芯片代工企业的毛利率则在20%左右。
值得注意的是,即便芯片代工行业的门槛非常高,但这并不意味着所有企业都能享有极高的毛利率或定价权。对于先进的制程技术(如28纳米以下的制程),只有少数几家顶级企业能够掌握,例如台积电和韩国的三星。这些企业为了保持领先地位,可能会采取降低价格的战略来压制竞争对手,尤其是那些专注于较落后制程的企业,这使得这些企业的定价权相对较弱,毛利率也相应较低。
最近,中芯国际计划投入480亿美元进行资本开支,以扩大产能和技术研发。由于电动汽车的兴起,对于低制程芯片的需求大幅增加,这也促使一些企业开始囤积芯片,导致市场上出现了低制程芯片的短缺现象,从而使得这些企业暂时处于较为有利的地位。
卡特尔模型(The Cartel Model)#
卡特尔模型假设市场上的企业相互合作(合谋)像垄断者一样进行决策,我们可以说这些企业构成了一个卡特尔组织。最著名的卡特尔是石油输出国组织(欧佩克,Organization of Petroleum Exporting Countries)。和古诺模型相比,卡特尔组织通过减产提价来获得更高的利润。
模型的基本设定如下:
市场的逆需求函数为:\(p=a-bQ, \quad b>0\);
有两家企业,成本函数为 \(c_i(q)\),\((i \in \{ 1,2\})\); 令 \(q_i\) 表示企业 \(i\) 的产出水平。
两家企业构成一个卡特尔组织。
卡特尔模型的市场均衡和拥有多家分厂的垄断企业的决策是一样的。如\numref{图%s
check
卡特尔内部的产量分配问题如图(a)和(b)所示,由企业的边际成本等于市场的边际收益所决定。因此,卡特尔均衡可以表示为:
显然,若两家企业的边际成本不相等,卡特尔可以通过调整企业之间的产量 — 边际成本低的企业增产,边际成本高的企业减产 — 来提高整体的利润水平。
代数上,我们可以将卡特尔的利润最大化问题表示为最大化两家企业的利润总和:
该问题的一阶条件表示企业的边际成本等于市场的边际收益:
虽然卡特尔的结果和垄断市场相同,但是需要注意,卡特尔的成员是具有法人资格的独立企业,他们会有自己的利益考量 — 考量的结果是增产(偏离卡特尔的最优产量)会使企业的利润增加。如\numref{图%s<>}所示,A点为卡特尔均衡,两企业等利润线相切,总利润最高,但是A点处的产量并没有在最佳反应曲线上。比如,给定 \(q_1^*\),企业2的最佳对应为 \(q_2'\),大于 \(q_2^*\) ;同理,给定 \(q_2^*\),企业1也有动力增产,偏离 \(q_1^*\)。
若两家企业因自利而选择增产,卡特尔组织便会分崩离析,因此,不同于垄断企业,卡特尔组织存在合作与自利的冲突,具有天然的脆弱性。卡特尔组织的减产提价协议并不能对成员进行有效约束,欧佩克成员国都曾违背过石油减产的承诺。
如果卡特尔组织可以对成员进行约束,使它们偏离的成本大于收益,那么便可以克服脆弱性问题。例如,\cite{reuben} 指出美国的医药行业是一个庞大的卡特尔组织,之所以鲜有成员偏离,是因为有着严苛的惩罚机制。
check Reuben (1958)
Kessel, Reuben. Price discrimination in Medicine. Journal of Law and Economics. 1958, (1): 20-53**
check
证明:卡特尔组织内的企业有动力偏离
证明:令 \((q_1^*,q_2^*)\) 为卡特尔模型中两企业的最优产量,我们要证明的问题可以表述为:在卡特尔市场的均衡下,给定企业2的产量,企业1增产会带来利润的增加。
给定企业2的产量,\(q_2^*\),企业1的利润可以表示为:
我们需要证明:
即企业1增产 (\(q_1>q_1^*\)) 会带来利润的增加。
由式(1)可得:
在\(q_1^*\)处的取值为:
对比卡特尔模型的一阶条件(式@ref{}) check
可以得到: $\( \frac{d \pi_1}{dq_1}|_{q_1^*} = bq_2^* >0 \)$
Q.E.D.
check
