最优选择的性质

收入和价格是消费者理论中外生给定的变量。研究外生变量变化对均衡影响的分析称为比较静态分析。

基于效用最大化问题，我们可以得到的商品最优选择（马歇尔需求函数），它是关于价格和收入的函数，如\(x_i^* = x_i(p_1,p_2,I)\)。在本部分，我们将分析收入变化和价格变化对最优选择的影响。其中，价格变化的影响是本章的重点，将回答是否可以由消费者理论推出需求定律的问题。

收入变化

假设消费者的效用函数为科布道格拉斯形式：\(u = x_1^a x_2^b\)，\(a\)，\(b\)为参数，两商品价格都为1，消费者收入为I。因为价格是定值，所以两商品的最优选择是关于收入的函数，代表了收入对最优选择的影响。在此例中，两商品的最优选择是关于收入的线性函数。

\[\begin{split} \begin{eqnarray*} x_1^* & =& \frac{a}{a+b}I\\ &&\\ x_2^* & =& \frac{b}{a+b}I \end{eqnarray*} \end{split}\]

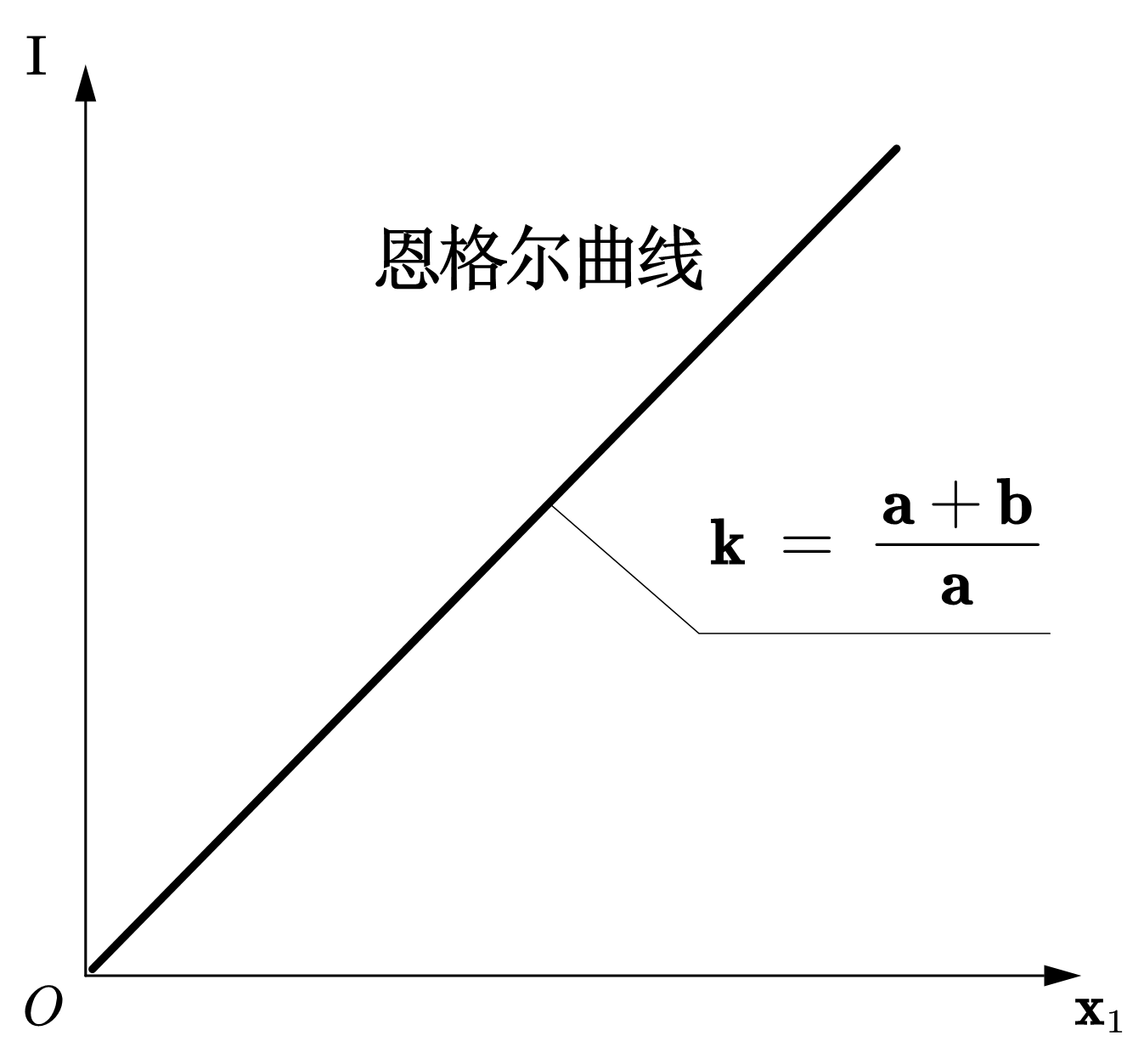
图54展示了收入（\(I\)）与商品1最优选择（\(x_1^*\)）的关系曲线，称为恩格尔曲线——表示商品的最优选择如何随收入的变化而变化。习惯上，我们用纵轴表示收入，横轴表示数量，但要注意的是收入变化是因，数量变化是果。

更一般而言，恩格尔曲线的表达式可以写为：\(x_i^* = x_i(\bar{p_1},\bar{p_2},I)\ \ i=1,2\)。

(a) 上例中商品1的恩格尔曲线。

(b) 一条可能的恩格尔曲线

Fig. 54 恩格尔曲线

下面，我们使用几何图对收入的影响进行分析。

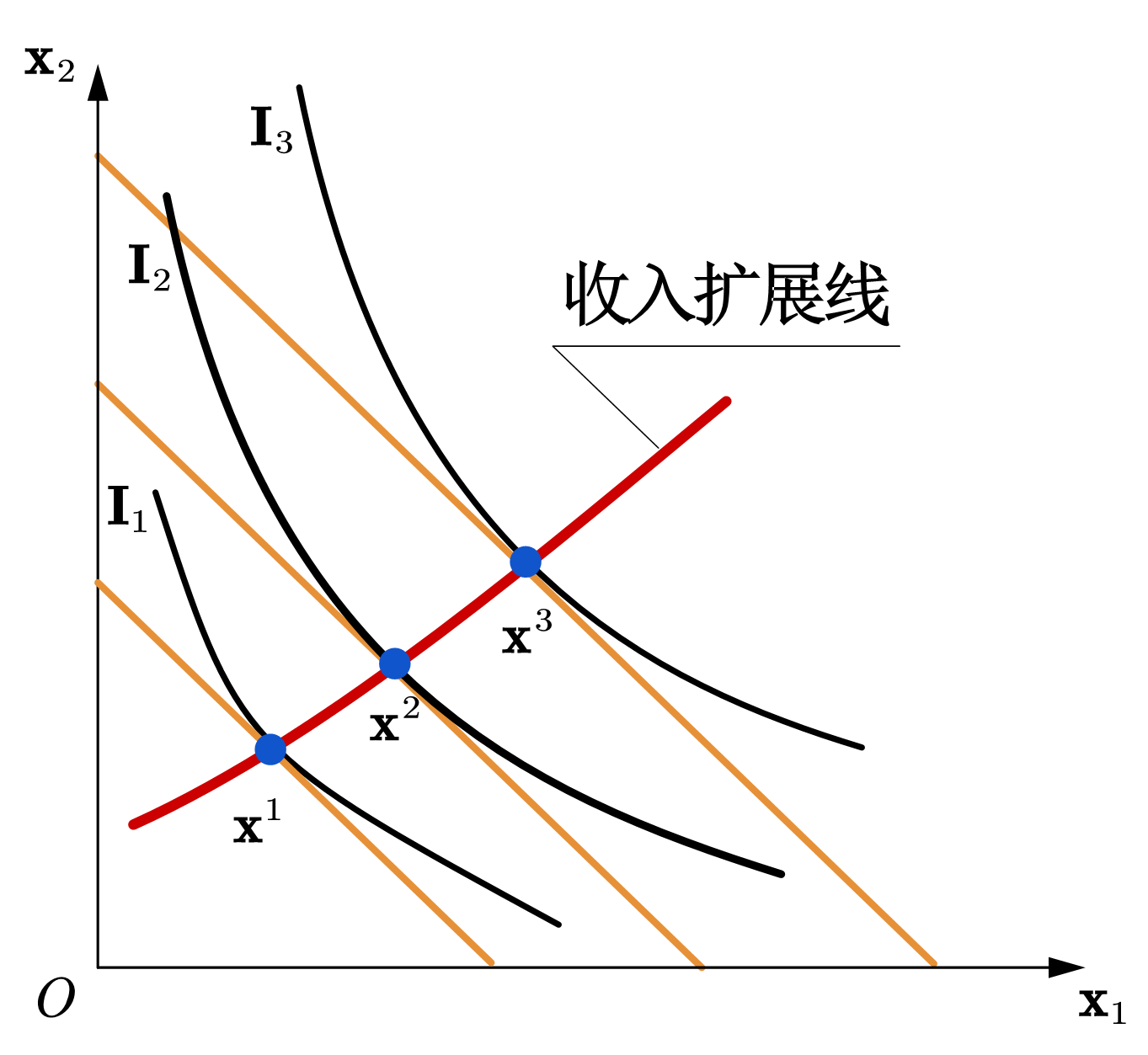
如图55所示，在消费集内，收入的变化对应的是预算线的平行移动，在每条预算线上，找到一条无差异曲线与之相切，切点即为最优消费束。将这些最优消费束相连所构成的曲线称为收入扩展线或收入-消费曲线或。 收入-消费曲线上的每一点都包含着某一收入水平下最优选择的信息。因此，我们可以通过收入扩展线来分析恩格尔曲线的性状。

科布道格拉斯形式效用函数的收入扩展线

如果效用函数采用科布-道格拉斯形式，那么商品支出的占比将会保持不变，因此收入扩展线将是一条直线。假设效用函数为：\(u = x_1^a x_2^b\)，则收入扩展线的表达式为：

\[ x_2 = \frac{bp_1}{ap_2}x_1 \]

\(p_1\)和\(p_2\)分别为商品1和2的价格，为定值。

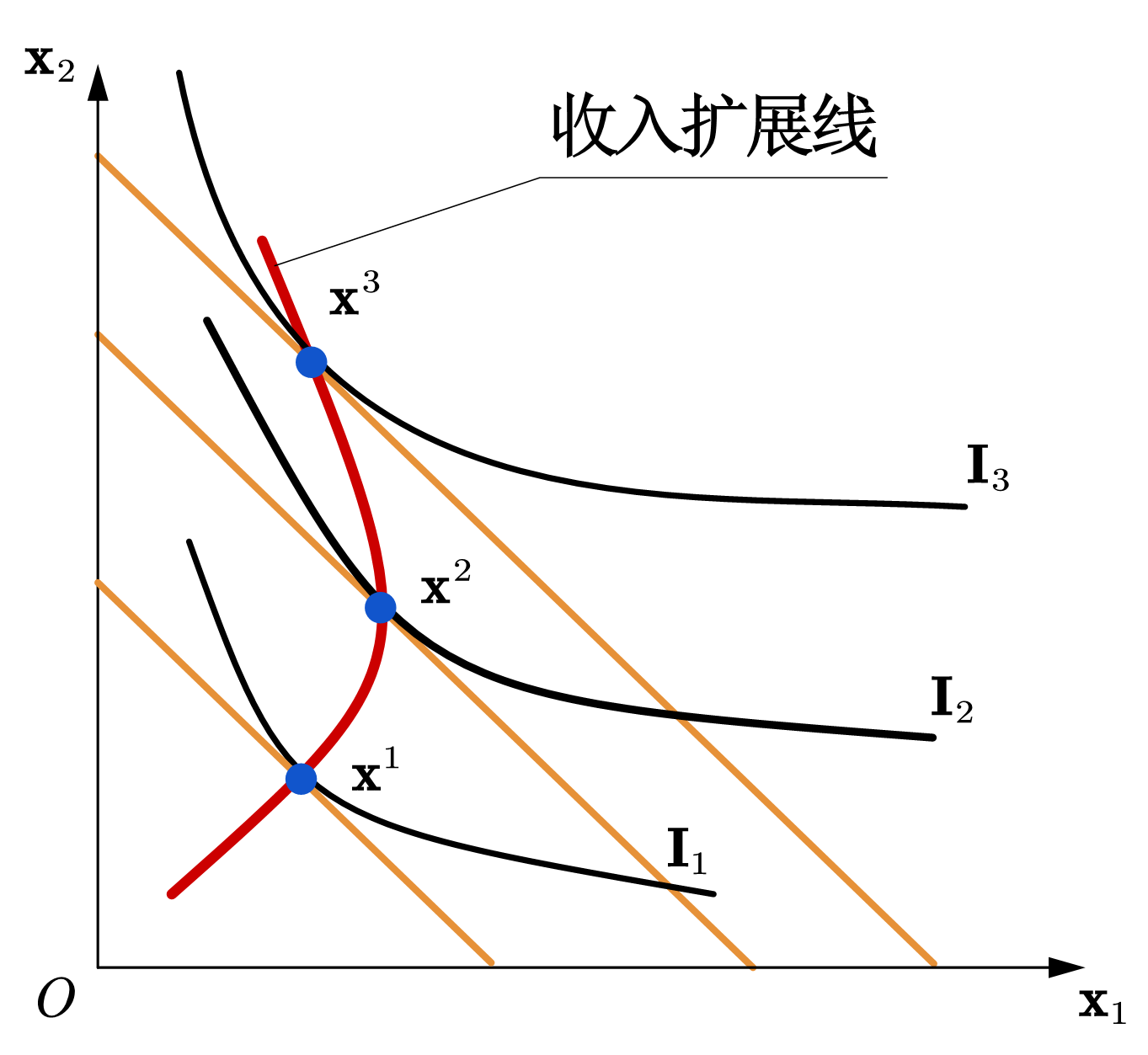
收入对最优选择的影响受到消费者偏好的约束，图(a)的收入扩展线表明最优消费束中的两种商品的数量都随着收入的上升而增加，呈现出正常商品（normal goods）的特征；图(b)中，收入-消费线向纵轴弯折，说明当收入增加到某一水平后，随着收入增加，商品1的最优数量是下降的，呈现出贫穷商品（inferior goods）的特征。

(a) 收入与商品1最优选择同向变化

(b) 收入与商品1最优选择先同向后反向变化

Fig. 55 收入扩展线 (黄色为预算线)

恩格尔系数和恩格尔定律

恩格尔系数：食物消费支出占总消费支出的比重，即食品支出/ 总支出×100，是衡量家庭消费支出结构的指标。如果恩格尔系数越高，说明家庭主要支出在生活必需品上，说明该家庭的生活水平比较低；如果恩格尔系数越低，说明家庭主要支出在非必需品上，说明该家庭的生活水平比较高。

恩格尔定律（Engel’s law）：经济学家恩格尔提出的一个经济学原理，它描述了随着收入增加，家庭支出结构或消费结构发生的变化。根据恩格尔定律，家庭在支出中用于食品和日用品的比例会随着收入增加而降低，而用于住房、娱乐、旅游、教育和医疗等方面的支出比例则会增加。这是因为人们在收入较低时会将大部分收入用于满足最基本的生活需求，如食物和日用品。但随着收入增加，人们的需求会逐渐转移到更高层次，在其他方面也会花费更多的钱。

价格变化

这里的分析思路也适用于价格变化对其它商品的影响，但在此不做探讨。

我们关注商品自身价格变化对其最优选择的影响。商品的最优选择与自身价格的关系为需求关系，如\(x_1(p_1,\bar{p}_2,\bar{I})\)与\(p_1\)的关系。如果商品自身价格和最优选择的数量负相关，则说明商品的需求曲线向右下方倾斜。

假设消费者的效用函数为\(U = x_1^ax_2^b\)，商品1和2的价格分别为\(p_1\)和\(1\),消费者收入为40, 我们可以得到商品1的需求函数：

\[ x_1^* = \frac{a}{a+b}\frac{40}{p_1} \]

显然，商品1的价量呈反向变化，符合需求定律。那么，是不是在所有的偏好下，价量都呈反向关系呢？我们先通过几何图做一下分析。

假设商品1的价格发生变化，商品2的价格和消费者收入为定值。如图56所示，在消费集中，商品1的价格变化会使预算线以纵轴交点为轴发生转动。在每条预算线上，找到一条无差异曲线与之相切，切点即为最优消费束。将这些最优消费束相连所构成的曲线被称为「价格-消费曲线」。提取价格-消费曲线上每一点所对应的商品1的价量信息，将它们的关系表示在价格-数量的坐标系中，便为商品1的需求曲线。

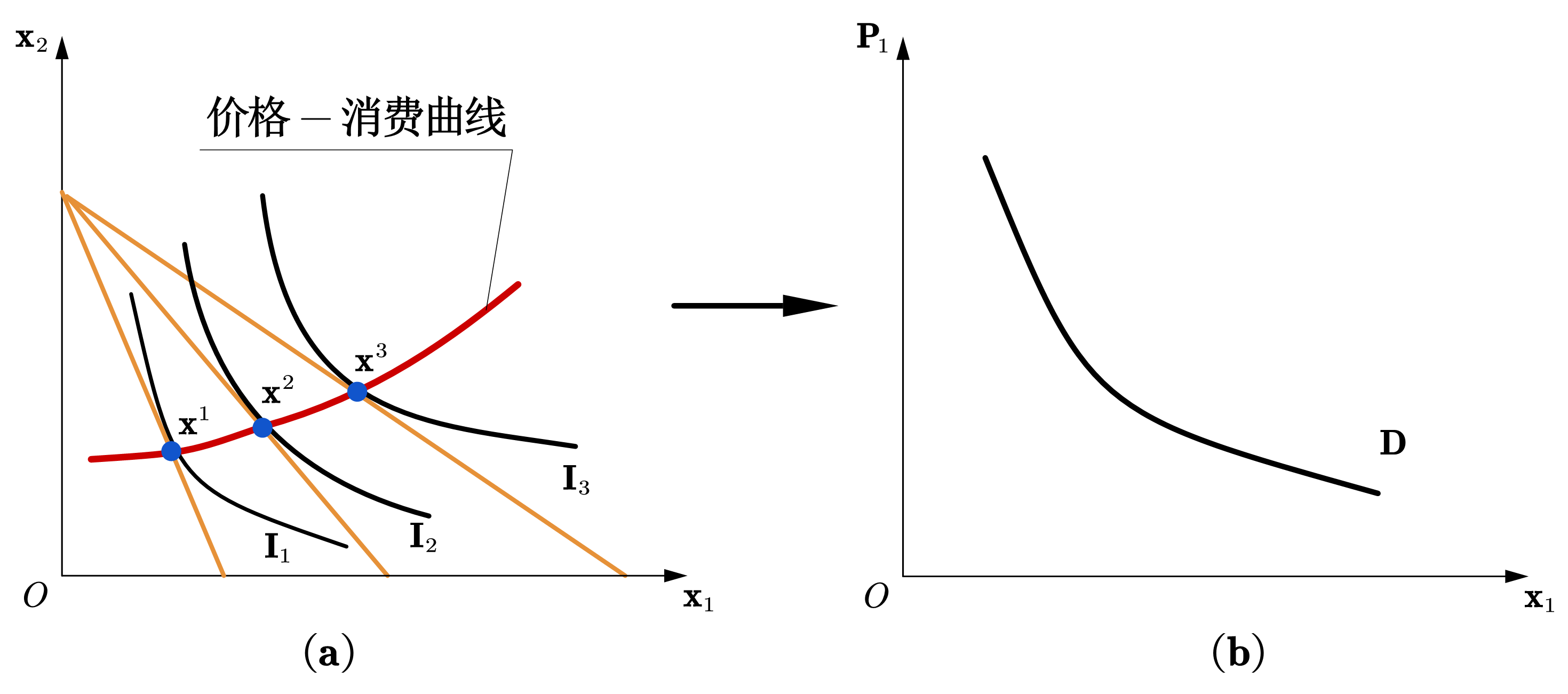
Fig. 56 价格-消费曲线 （黄色为预算线）

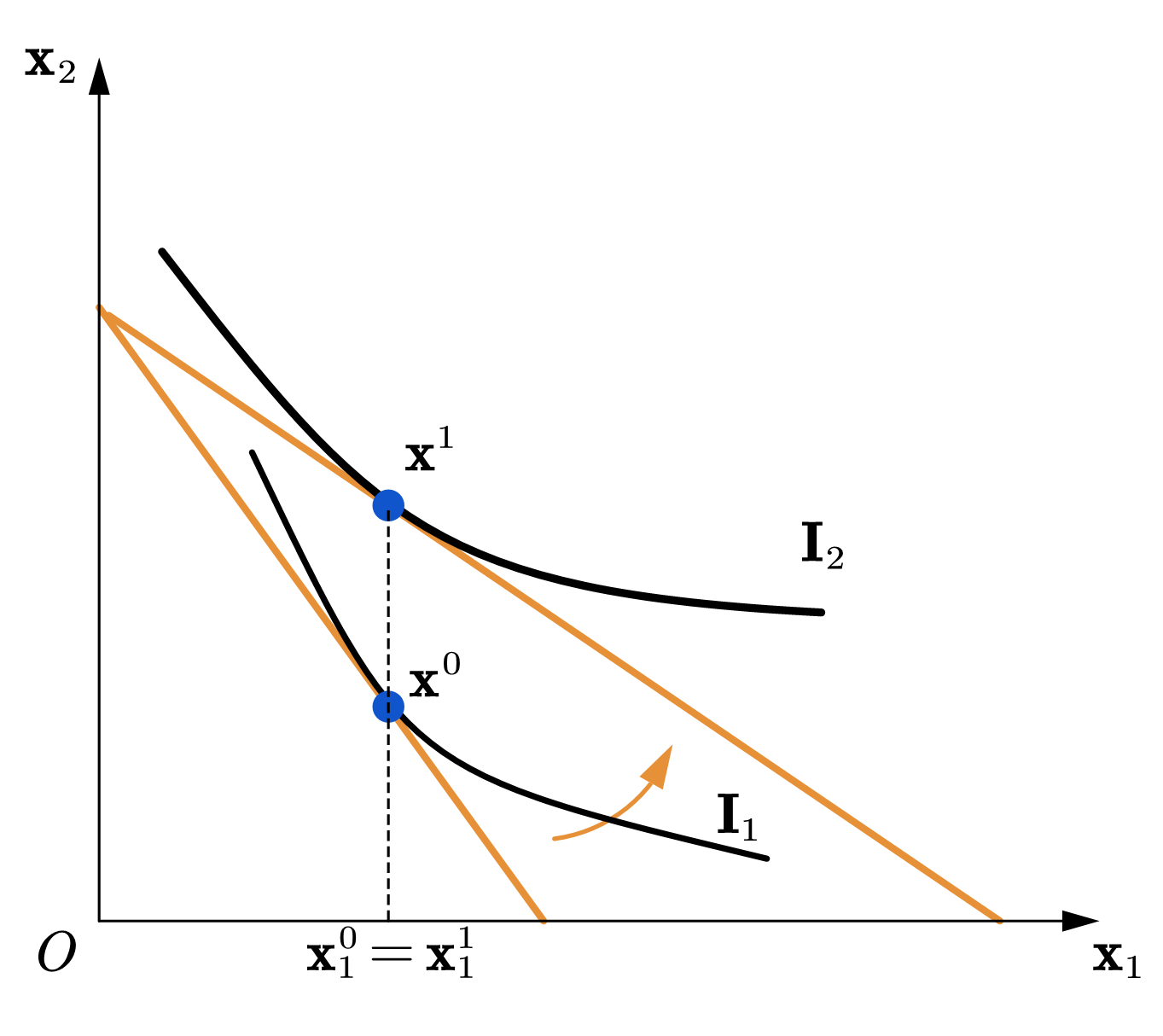
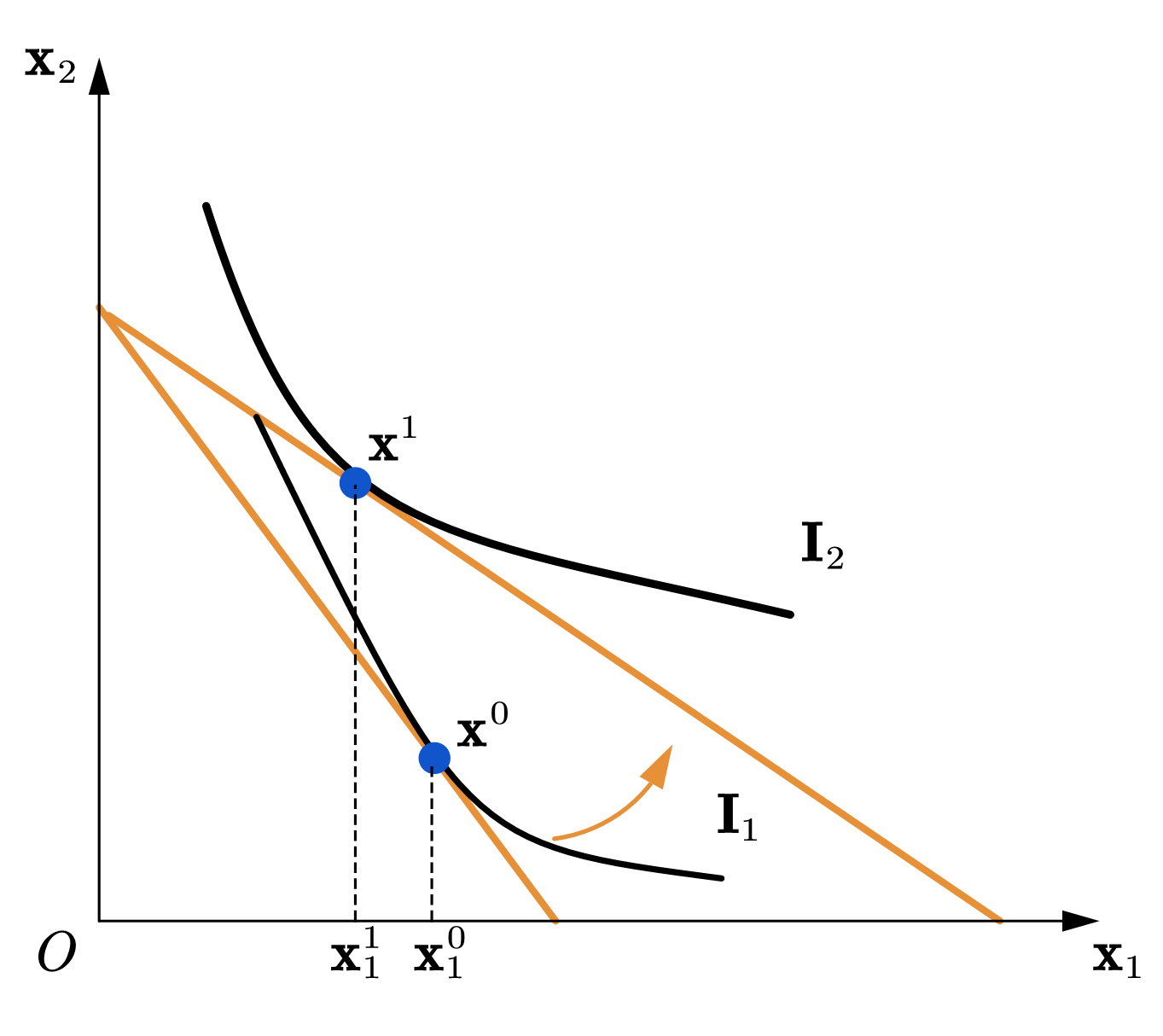
我们可以使用价格-消费曲线来分析需求曲线的性状。如图57所示，当商品1的价格下降时，在不同的偏好下，商品1的需求量有可能会上升（图(a)），保持不变（图(b)）或下降（图(c)）。这些变化都符合效用最大化问题的最优条件：\(MRS_{12}=\frac{P_1}{P_2}\) ，同时也在预算线上。之所以价量关系不是确定的，是因为当商品1的价格变化后，新的最优消费束会跳到另一条无差异曲线（与新的预算线相切）上，消费者理论只约束了在同一条无差异曲线上的MRS递减，而在不同无差异曲线上，MRS随商品数量变化的关系是不确定的。例如，商品1的价格下降会导致最优消费束处\(MRS_{12}\)下降，但商品1的数量会如何变化是理论上无法确定的。

(a)

(b)

(c)

Fig. 57 商品1价格变化对最优选择的影响。

由此，我们可以得到如下结论：

• 在不同的偏好下，价量关系可以是负向或正向的关系。

• 由消费者理论不能推出需求定律。

针对不同偏好下价量关系的不确定性，我们需要进一步探究，消费者理论能否为价量关系提供一些确定性的推断？我们需要了解在某些商品特征下，我们是否可以推断其价量关系?此外，由消费者理论推出的价量同向变化的现象，可以称为“吉芬现象”或“吉芬悖论”（Giffen Paradox）。我们也需要思考该现象是否证伪了需求定律？以及应如何处理“吉芬现象”。

替代效应和收入效应

我们称价格变化对最优选择的影响为总效应（Total Effect, TE）。进一步地，我们将总效应分解为替代效应（Substitution Effect, SE）和收入效应（Income Effect, IE）两个子部分，并对它们进行分析（分而治之的思路）。分解的目的是使子部分具有较好的随价格变化的特征，以便更容易推断总效应的变化方向。

• 替代效应（Substitution Effect, SE）：实际收入（实际购买力）不变时，价格变化对最优选择的影响。

• 收入效应（Income Effect, IE）：价格不变时，实际收入变化对最优选择的影响。

  • 收入效应 = 总效应 - 替代效应

在具体应用时，有两种分解方法：斯勒茨基分解（The Slutsky decomposition）和希克斯分解（The Hicksian decomposition）。两者的区别在于对实际收入的定义：前者是从消费束的角度定义实际收入，实际收入不变是指 价格变化后，消费者原来的最优消费束恰可负担；后者是从效用的角度定义实际收入，实际收入不变是指 价格变化后，消费者的效用水平不变。相应的，我们将基于这两种方法计算的替代效应分别称为「斯勒茨基替代效应」和「希克斯替代效应」。

价格变化对实际收入的影响

无论是用消费束还是效用定义实际收入，价格变化都与实际收入负相关——价格下降，实际收入上升，价格上升，实际收入下降。

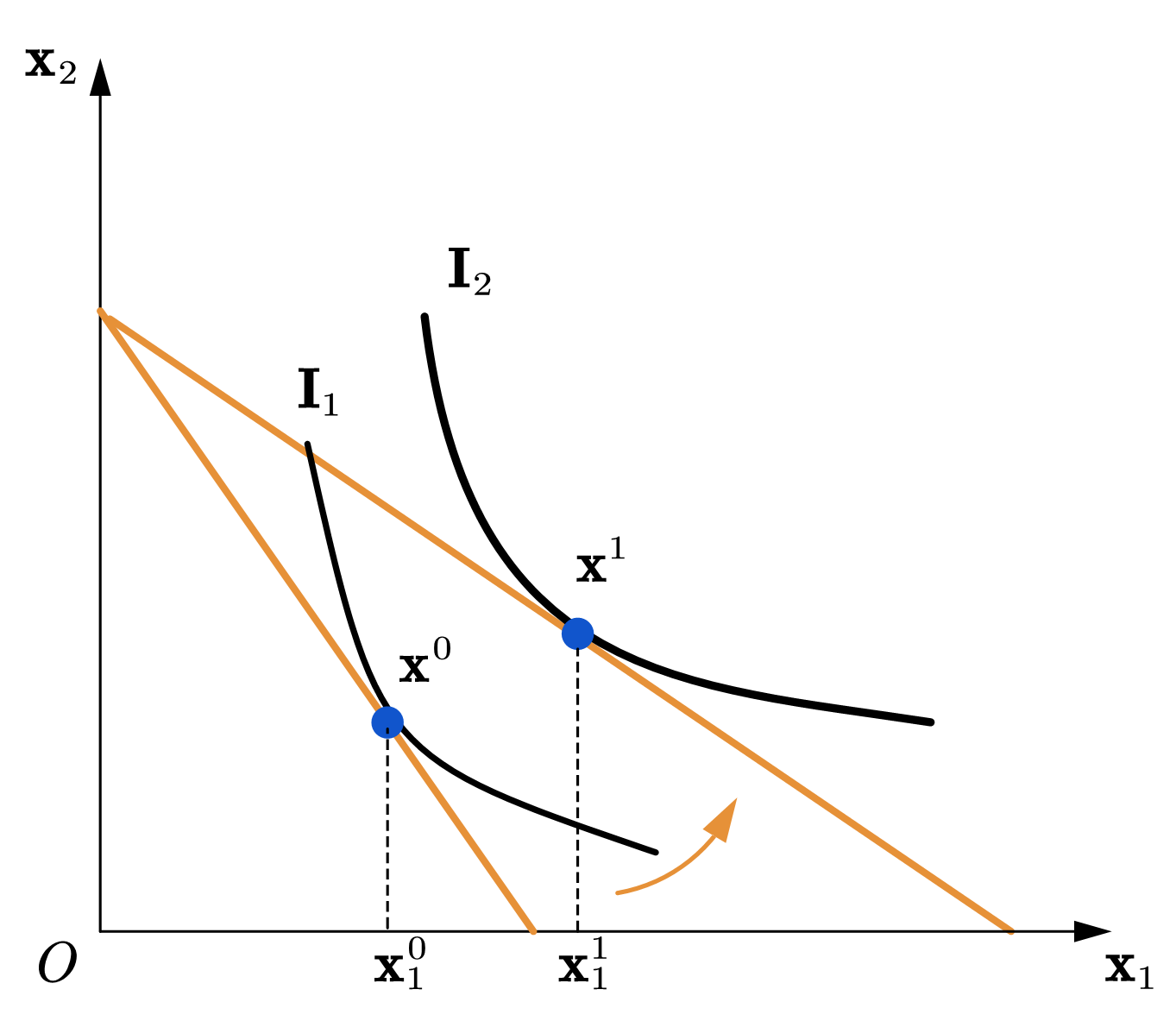
如图57所示， 当商品1的价格下降时，预算线向外扰动，最优选择由消费束\(x^0\)变为\(x^1\), 很显然，\(x^1\)对应的效用水平更高，同时，在新的价格下，消费者若购买消费束\(x^0\)，收入仍有所余（因为\(x^0\)在新的预算线内部），两者皆说明消费者的实际收入上升。

同理，如果商品1的价格上升，预算线向内扰动，最优选择由消费束\(x^1\)变为\(x^0\), 这时，\(x^0\)对应的效用水平更低，同时，在新的价格下，消费者的收入不足以购买消费束\(x^1\)（因为\(x^1\)在新的预算线外部），两者皆说明消费者的实际收入下降。

为了便于后续分析，我们将商品1和2的初始价格分别记为\(p_1\)和\(p_2\)（也称为原价格）, 收入为\(I\)，最优选择为\(x_1^0\)和\(x_2^0\),效用水平为\(u^0\)。再假设商品1的价格由\(p_1\)下降为\(p_1'\)（也称为新价格），商品2的价格不变。

如图58所示，AB为原价格下的预算线，斜率为\(-p_1/p_2\)，最优选择为\(\mathbf{x}^0\)，是AB与无差异曲线的切点，该无差异曲线的效用为\(u^0\)。AC为新价格下的预算线，斜率为\(-p_1'/p_2\)，最优选择为\(\mathbf{x}^1\)，是AC与无差异曲线的切点，总效应为消费束\(\mathbf{x}^0\)到\(\mathbf{x}^1\)所对应的商品1的数量变化，即：

\[ \text{TE} = x_1(p_1',p_2,I)-x_1(p_1,p_2,I) = x_1^1 - x_1^0 \]

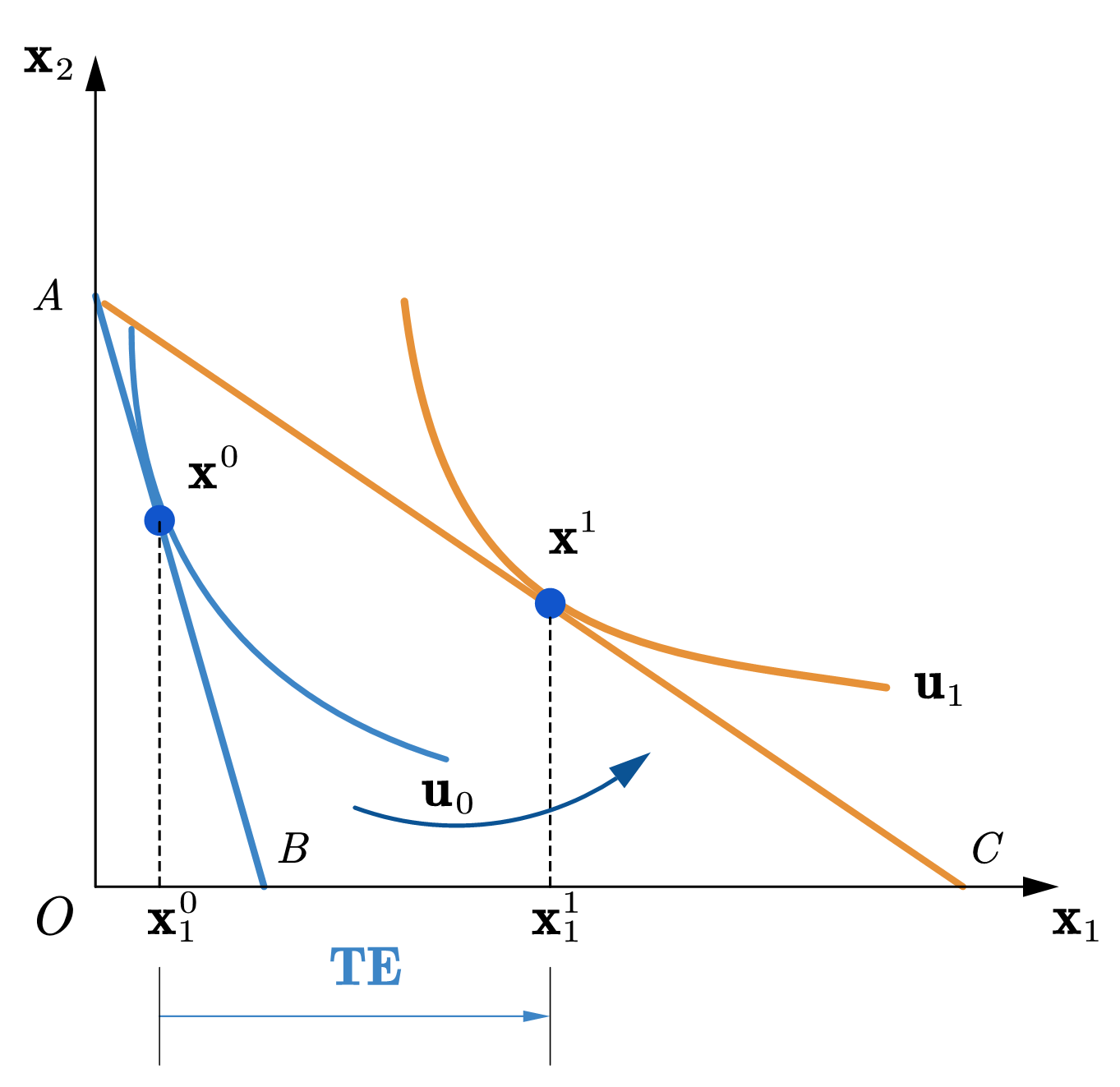
Fig. 58 总效应

斯勒茨基分解

之所以要求原消费束恰可负担，是因为如果收入有所余，则说明实际收入上升，若收入不足，则说明实际收入下降。

斯勒茨基替代效应为在原最优消费束恰可负担的情况下，商品价格变化所引起的需求量的变化。为了计算替代效应，我们需要计算在\((x_1^0, x_2^0)\)恰可负担的前提下，消费者的最优选择，对应的效用最大化问题为：

\[\begin{split} \begin{array}{c}\max_{x_1,x_2} \ u(x_1,x_2) \\ \\s.t. \quad p_1'x_1 + p_2x_2 = p_1'x_1^0 + p_2 x_2^0 \end{array} \end{split}\]

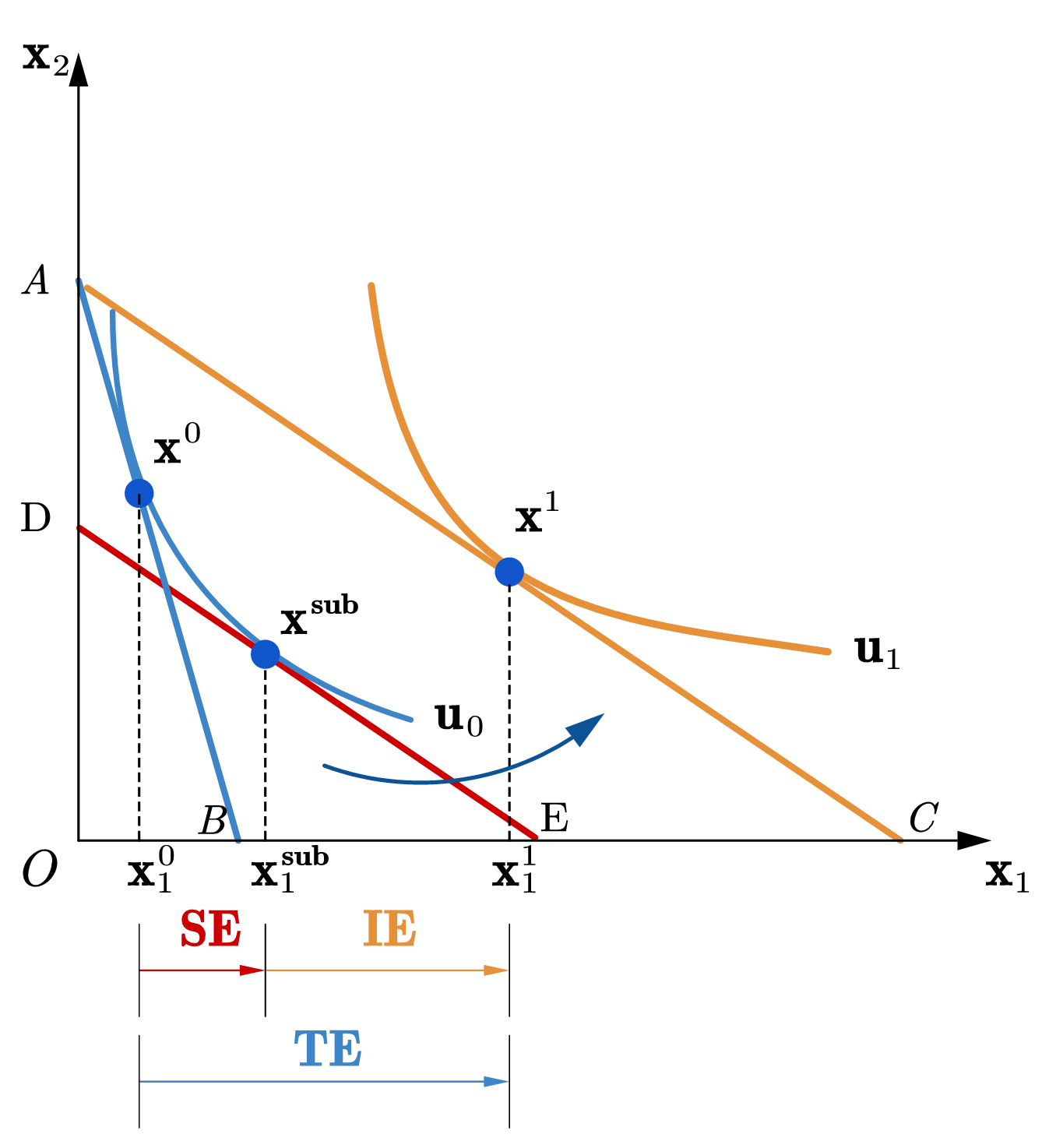
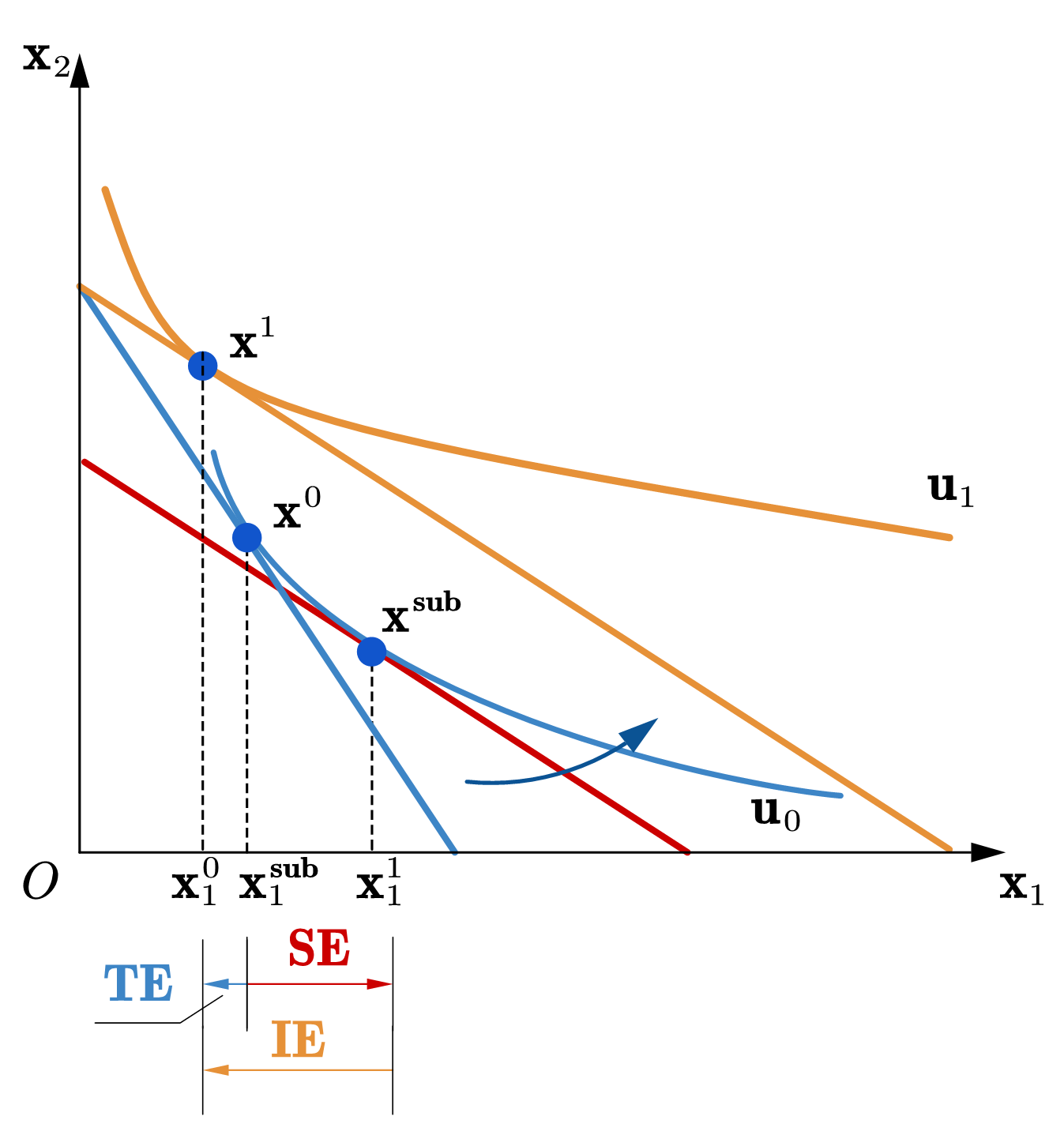
令\(I' = p_1'x_1^0 + p_2 x_2^0\)，表示原消费束恰可负担的收入水平，由新价格和原消费束所决定，如图59 (a)所示，对应的预算线为\(DE\)，可以称为辅助预算线。辅助预算线的斜率为\(-p_1'/p_2\)，与新价格下的预算线\(AC\)平行，且通过原最优选择，\(\mathbf{x}^0\)。点\(\mathbf{x}^{sub}\)为辅助预算线上的最优选择，所对应的商品1的数量为 \(x_1^{sub} = x_1(p_1', p_2, I')\)。

依据定义，由原价格下的预算线\(AB\)到辅助预算线\(DE\)对应的是实际收入不变，价格变化的影响；由辅助预算线\(DE\) 到新价格下的预算线\(AC\)对应的是价格不变，实际收入的变化，因此，由\(\mathbf{x}^{sub}\)到\(\mathbf{x}^0\)所对应的商品1的数量变化为（斯勒茨基）替代效应，由\(\mathbf{x}^{sub}\)点到\(\mathbf{x}^{1}\)所对应的商品1的数量变化为收入效应，即

\[\begin{split} \begin{eqnarray*} SE &=& x_1(p_1',p_2,I') - x_1(p_1,p_2,I) &= & x_1^{sub} - x_1^0 &\\ IE &=& x_1(p_1',p_2,I) - x_1(p_1',p_2,I') &=& x_1^1 - x_1^{sub} &= TE - SE \end{eqnarray*} \end{split}\]

(a) 斯勒茨基分解

(b) 希克斯分解

Fig. 59 替代效应和收入效应

希克斯分解

希克斯替代效应是指，在原效用水平不变的前提下，商品价格变化所引起的需求量的变化。为了计算替代效应，我们需要求解效用水平为\(u^0\)时，消费者的最优选择，这可以表示为一个支出最小化问题：

\[\begin{split} \begin{eqnarray*} \min_{x_1,x_2}\ p_1'x_1+p_2x_2 \\ s.t. \quad u(x_1, x_2) = u^0 \end{eqnarray*} \end{split}\]

支出最小化问题（Expenditure Minimization Problem, EMP）

支出最小化问题是指当效用为定值时，消费者找哪个消费束支出最小的问题。为了求解这个问题，我们首先定义等支出线 —— 使支出不变的消费束的连线，在消费集中，我们可以画出无数条等支出线。等支出线向外移动，支出增加，向内移动，支出减少。

支出最小化问题可以转化为固定无差异曲线（效用水平不变），移动等支出线的问题。无差异曲线上的每一个消费束，都可以画出一条等支出线。如图60所示，当等支出线与无差异曲线相切时，所对应的消费束支出是最小的。我们可以写出相应的代数条件：

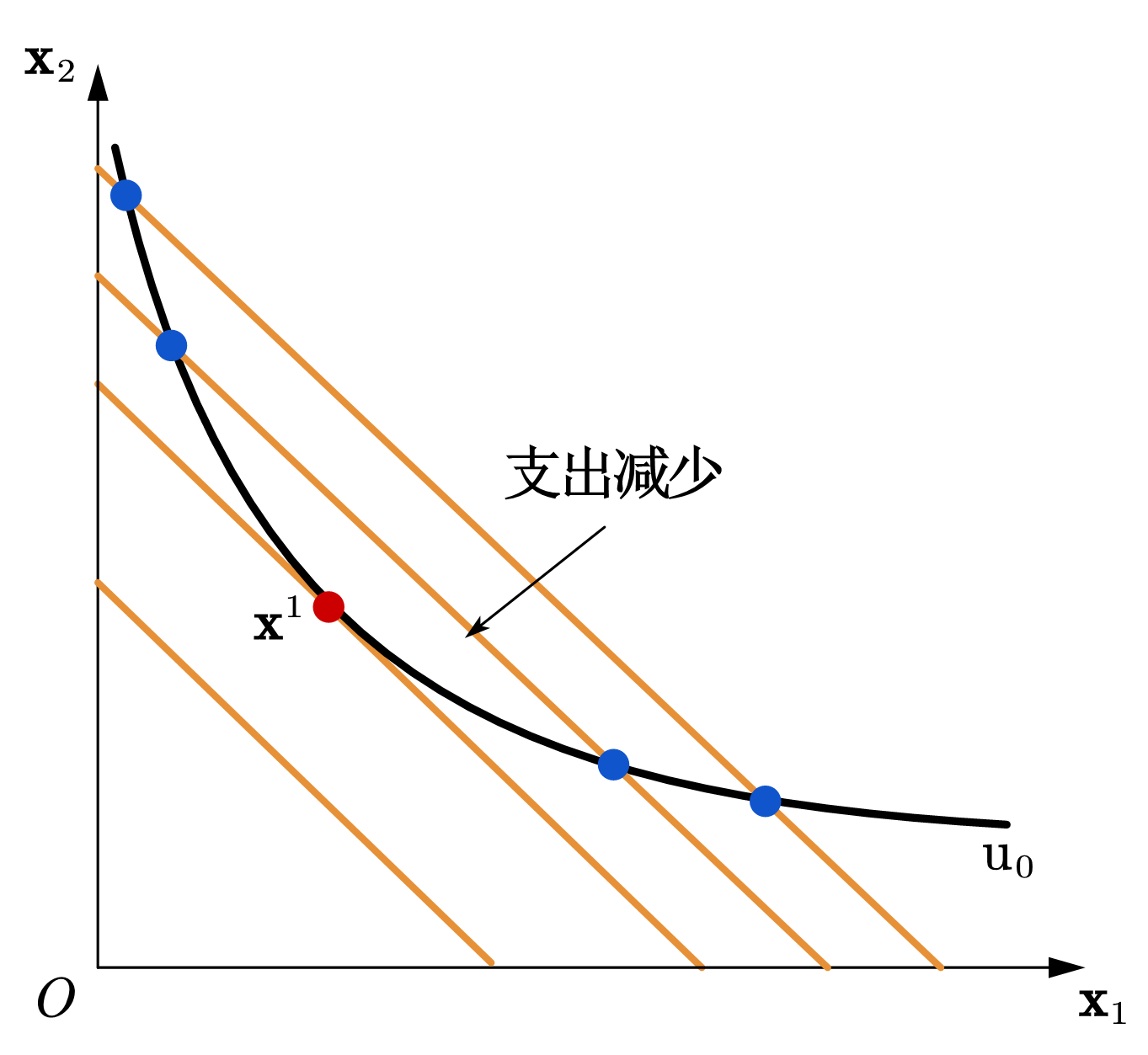
Fig. 60 支出最小化问题：找到一条等支出线与固定的无差异曲线相切，切点即为支出最小的消费束。

• 预算线斜率的绝对值与商品1对商品2的边际替代率相等：

\[ MRS_{12} = \frac{p_1}{p_2} \]

• 最优选择的效用水平为给定的效用值：

\[ u(x_1, x_2) = u^0 \]

最优选择是关于商品价格和效用的函数，称为希克斯需求函数（Hicksian Demand）：

\[\begin{split} \begin{align} x_1^* &= & x_1(p_1, p_2, u^0)\\ x_2^* &= & x_1(p_1, p_2, u^0) \end{align} \end{split}\]

相应的，最小支出记为\(e(p_1,p_2,u)\)：

\[ e(p_1,p_2,u) = p_1x_1(p_1,p_2,u^0) + p_2x_2(p_1,p_2,u^0) \]

---

支出最小化问题和效用最大化问题的最优条件都是相切，两者本质上是一个对偶问题。

• 如果给定效用最大化问题中的最大效用值，支出最小化问题的最小支出等于效用最大化问题中的给定的收入。

• 如果给定支出最小化问题中的最小支出，效用最大化问题的最大效用等于支出最小化问题中给定的效用。

\[\begin{split} \begin{align} e(p, u(p,m)) = m \\ u(p, e(p,u)) = u \end{align} \end{split}\]

\(u(p,m) = u(x_1(p,m), x_2(p.m))\) 为效用最大化问题的最大效用值。

求解支出最小化问题需要找到一条等支出线与原无差异曲线相切，如图59 (b)中的\(DE\)，斜率为\(-p_1’/p_2\)，与新价格下的预算线\(AC\)平行。我们也将其记为辅助预算线，反应了实际收入不变（原效用水平不变）的含义。切点所对应的消费束\(\mathbf{x}^{sub}\)即为支出最小化问题的解（最优选择），所对应的商品1的数量为 \(x_1^{sub} = x_1(p', p_2, u^0)\)。

与上面的分析相同，由原价格下的预算线\(AB\)到辅助预算线\(AD\) 对应的是实际收入不变，价格变化的影响；由辅助预算线\(AD\) 到新价格下的预算线\(AC\)到代表了价格水平不变，实际收入的变化，得到的替代效应和收入效应分别为：

\[\begin{split} \begin{eqnarray*} SE &=& x_1(p_1',p_2, u^0) - x_1(p_1,p_2,I) & = & x_1^{sub} - x_1^0 &\\ IE &=& x_1(p_1',p_2,I) - x_1(p_1',p_2, u^0) & = & x_1^1 - x_1^{sub} & = TE - SE \end{eqnarray*} \end{split}\]

如何在消费集中标记替代和收入效应?

首先，画出价格变化前后的预算线。

其次，画出辅助预算线，即使实际收入不变所对应的预算线或等支出线。

• 斯勒茨基SE：辅助预算线与新预算线平行，且通过原最优选择。

• 希克斯SE：辅助预算线与新预算线平行，且与原效用最大化的无差异曲线相切，这条切线为支出最小的等支出线。

再次，在辅助预算线上，找出最优消费组合。

• 斯勒茨基SE：在辅助预算线上，画出一条与之相切的差异曲线，切点为实际收入不变的最优选择。

  • 注意这里画出的无差异曲线不能与原无差异曲线相交。

• 希克斯SE：辅助预算线与原无差异曲线的切点为实际收入不变的最优选择。

最后，从原预算线到辅助预算线，商品最优选择变化为替代效应，从辅助预算线到新预算线商品最优选择的变化为收入效应。在不同的分解方法下，因为辅助预算线的位置有所不同，所以计算出的替代效应与收入效应在数值上会存在差异。

替代效应、收入效应与价格变化的关系

尽管斯勒茨基分解和希克斯分解计算的替代效应和收入效应的数值会存在差异，但它们随价格变化的特征是一致的。

定理3-1：替代效应必与价格的变化方向相反。

定理3-2：对于正常商品，收入效应与价格的变化方向相反；对于贫穷商品，收入效应与价格的变化方向相同。

我们基于希克斯替代效应证明定理3-1，大家可以自己尝试使用斯勒茨基替代效应进行证明。

证明定理3-1：希克斯替代效应与价格的变化方向相反

首先，无论商品1的价格如何变化，最优选择\((x_1^*,x_2^*)\)都满足：

\[𝑴𝑹𝑺_{𝟏𝟐}=p_𝟏/p_𝟐\]

表明最优选择处的 \(𝑴𝑹𝑺_{𝟏𝟐}\)与\(p_1\)同向变化。

其次，因为无差异曲线严格凸向原点，所以在同一条无差异曲线上，\(𝑴𝑹𝑺_{𝟏𝟐}\)与 \(𝒙_𝟏\)反向变动。

再次，基于希克斯替代效应的定义，辅助预算线上的最优选择与原最优选择在同一条无差异曲线上，因此，为了满足\(𝑴𝑹𝑺_{12}=p_𝟏/p_𝟐\) ，替代效应必然与\(p_𝟏\)反向变动。

\[ MRS_{12}=\frac{P_1}{P_2} \Rightarrow P_1\uparrow \rightarrow MRS_{12}\uparrow \rightarrow x_1\downarrow \Rightarrow \text{SE}<0 \]

证明定理3-2

首先，商品价格的上涨或下跌方向与实际收入变化的方向相反。因此，从辅助预算线到新价格下的预算线的收入变化与价格变化方向相反。

其次，对于正常商品，收入与最优选择同向变化；对于贫穷商品，收入与最优选择反向变化。

结合以上两点，可以得出结论：正常商品的收入效应与价格变化方向相反；贫穷商品的收入效应与价格变化方向相同。

由定理3-1和3-2可以推出，正常商品的需求曲线必然向右下方倾斜，而贫穷商品的需求曲线的方向不能确定：当替代效应为主时，需求曲线向右下方倾斜，当收入效应为主时，需求曲线将会向右上方倾斜，出现价量齐升的现象。

• 正常商品：

  \[\frac{\partial SE}{\partial p_i} <0 ,\ \frac{\partial IE}{\partial p_i} <0 \Rightarrow \frac{\partial TE}{\partial p_i} <0\]

• 贫穷商品：

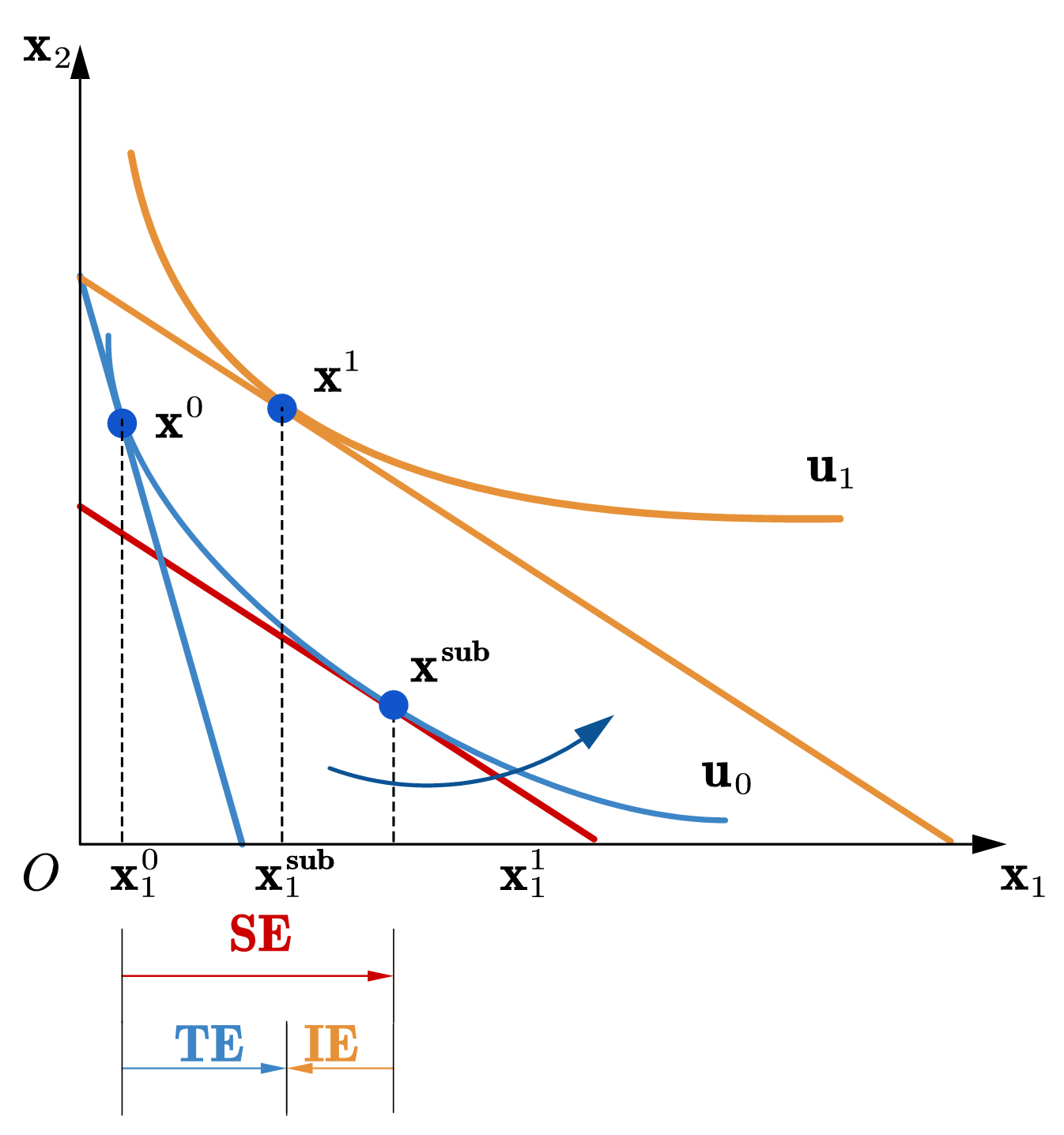
  \[\frac{\partial SE}{\partial p_i} <0 ,\ \frac{\partial IE}{\partial p_i} > 0 \Rightarrow \frac{\partial TE}{\partial p_i} \ \text{方向不确定}\]

(a) 总效应与价格变化方向相反

(b) 总效应与价格变化方向相同

Fig. 61 希克斯分解：贫穷商品的替代效应和收入效应

因为消费者理论描述的是个人的消费选择问题，推出的是个人的需求曲线，所以我们将价格变化引起消费者选择同向变化的现象称为「吉芬行为」（Giffen Behavior）。如果由个人需求曲线加总而得的市场需求曲线仍向右上方倾斜，则将所对应的商品称为「吉芬商品」（Giffen Goods）。

Jensen & Miller (2008)原文：“we should not expect to observe Giffen behavior at the market level; a subset of consumers might exhibit Giffen behavior with respect to a particular commodity while the overall market exhibits downward sloping demand. Thus, the search should not be for a Giffen good, but for Giffen behavior”.

吉芬商品关注的是商品的特征。商品的价量齐升现象也可称为吉芬现象或吉芬悖论（Giffen Paradox）。如果假设消费者是同质的，吉芬行为可以推出吉芬商品，但是，在现实中，却不是必然的，应该加以区分。如[]所述：“我们不应该期望在市场层面上观察到吉芬行为；一部分消费者可能会对某种商品表现出吉芬行为，而整个市场的需求曲线则呈现下降趋势。因此，我们不应该寻找吉芬商品，而是要寻找吉芬行为。”

需要注意的是，虽然我们不能对贫穷商品的价量关系做出确定性的推断，但如果商品的价量关系同向变化，那么该商品必为贫穷商品。换言之，贫穷商品是吉芬现象或吉芬商品出现的必要非充分条件。这一点可以作为我们判断商品的需求是否违反需求定律的思路。例如，一些网上文章将奢侈品和商品房称为吉芬商品，这显然是不正确的，因为奢侈品和商品房属于正常商品（高收入这才能购买），它们不是贫穷商品，因此必然不是吉芬商品。