消费者和生产者盈余

消费者和生产者盈余#

盈余代表的是买卖双方在市场交易中所获得的净好处，属于买方的称为消费者盈余（Consumer Surplus, CS），属于卖方的称为生产者盈余(Producer Surplus, PS)。很多书上将Surplus称为剩余，即将CS和PS分别称为消费者剩余和生产者剩余，与之相比，盈余听起来会更正向一些，所以我们这里使用盈余一词。

市场中各方盈余的加总被称为社会总盈余（Total Surplus, TS），这是福利经济学用于判断资源配置是否有效率的标准。如果资源配置可以最大化总盈余，则被视为是有效率的，反之，则为无效率。

在本部分，我们将会学习消费者和生产者盈余的定义和计算方法，以及它们分别与需求和供给曲线的关系。之后，我们会对市场均衡进行简单的福利分析，即其均衡产出是否是有效率的？

消费者盈余（Consumer Surplus）#

需求曲线上的价格#

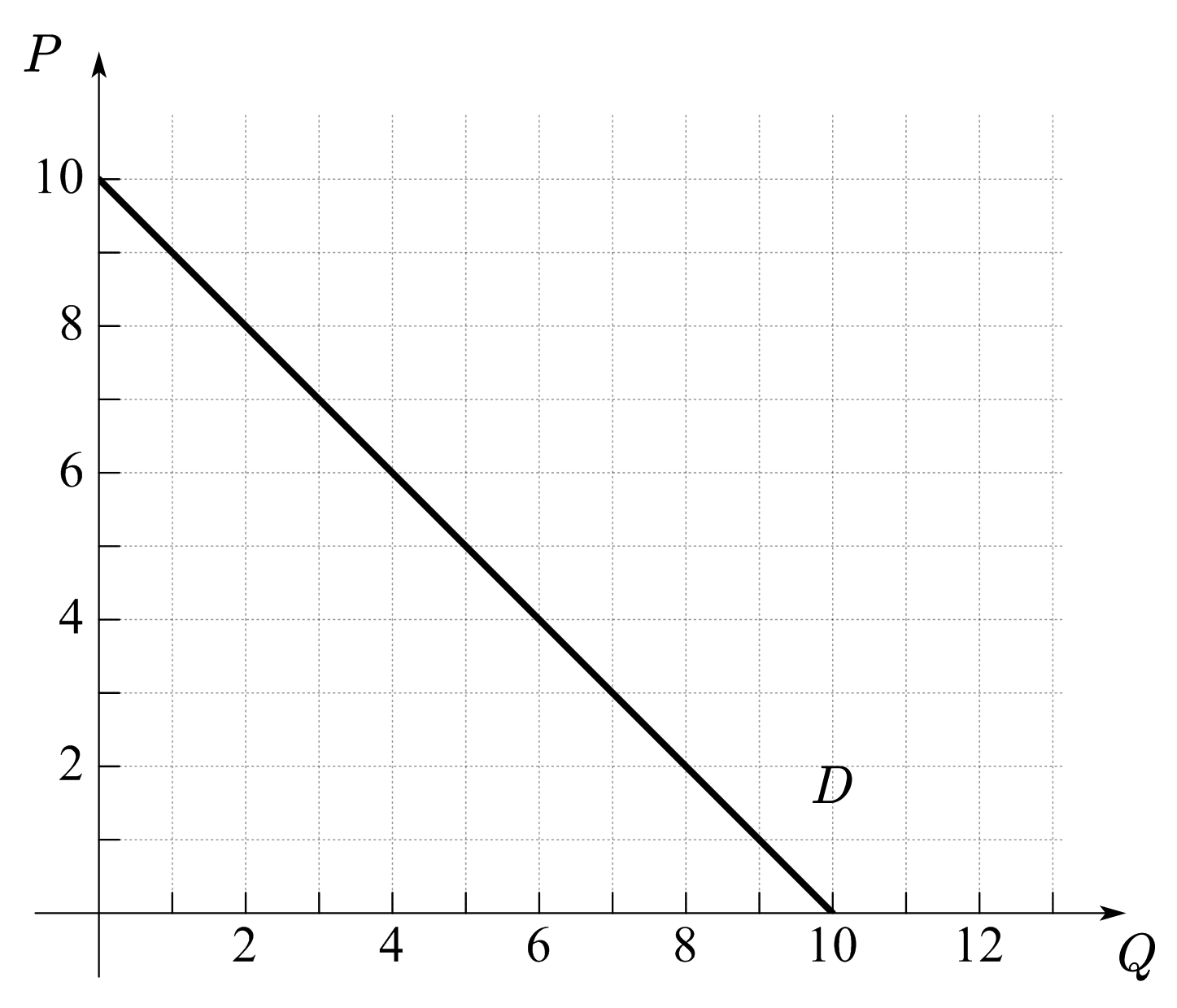
在需求部分，我们学习了需求曲线。需求曲线是需求关系的几何表示，代表了在不同价格水平下，消费者愿意且能够购买的最大数量。如图30(a)所示，当商品价格为9元，消费者最多愿意购买1单位商品。在消费者购买了1单位商品后，只有当商品价格降低到8元时，消费者才会愿意再购买一单位商品（总计2单位）。同理，当购买了2单位商品后，只有当商品价格降低到7元时，消费者才会愿意再增加一单位商品的购买（总计3单位）。

因此，从增加单位消费的角度看，我们可以将需求曲线上的价格理解为买方增加一单位商品购买的最高出价，又因为出价必然不会超过商品在买方心中所值，所以最高出价也代表了商品在消费者心中所值或商品给消费者带来的最大好处。相应的，图30(a)中的需求曲线也可以理解为，消费者对第一单位商品的最高出价为20元；由1单位增加至2单位时，最高出价为18元；由2单位增加至3单位时，最高出价为16元，依次类推。

增加一单位称为边际，我们可以将需求曲线上的价格称为消费者的边际支付意愿（Willingness To Pay，WTP，参见[]），边际保留价格（Reserve Price，参见[]），或边际用值（参见[]）。

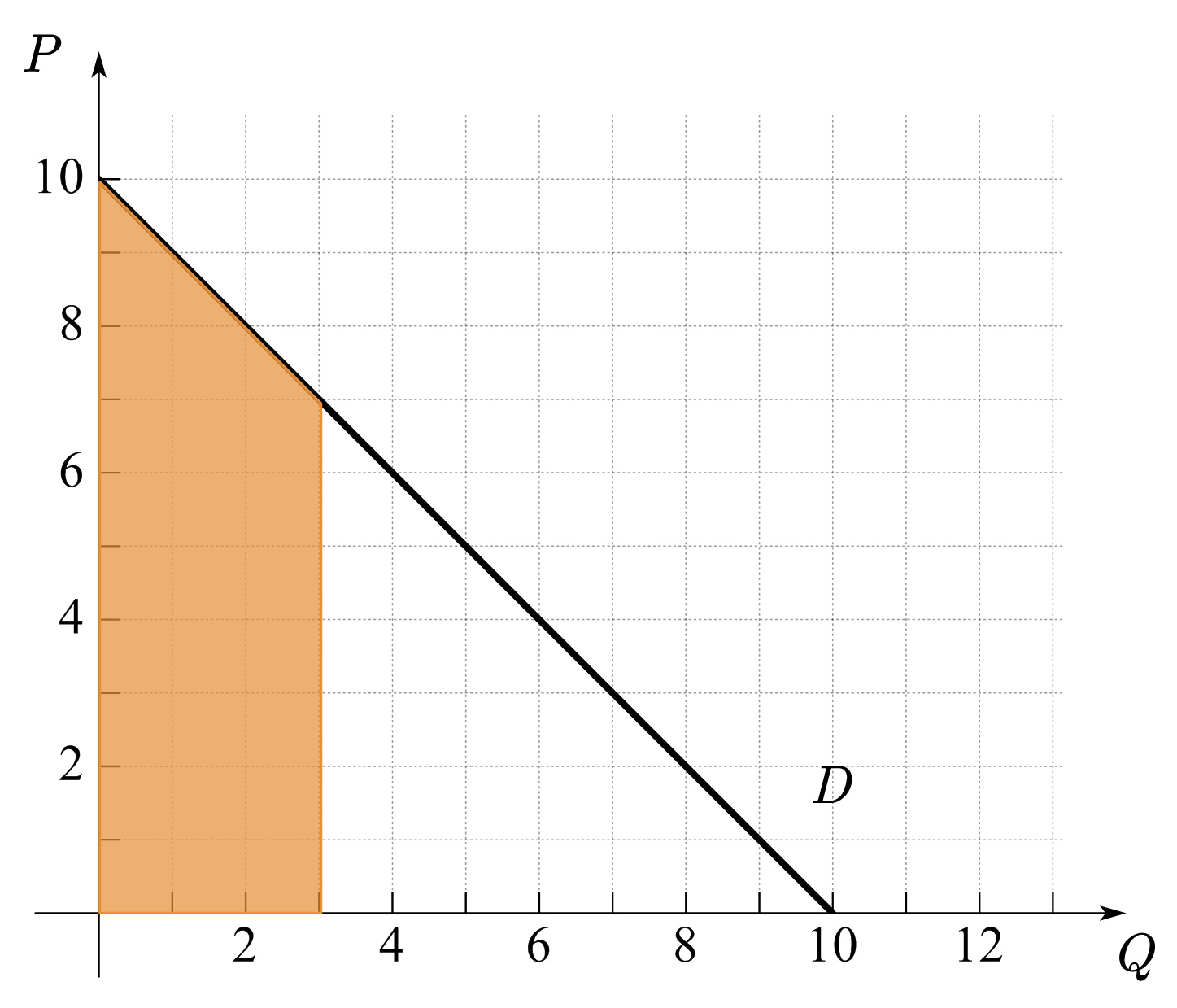
给定商品数量，消费者愿意支付的最高总价格为边际支付意愿的加总。在图30(a)中，若消费者想购买3单位商品，其愿意支付的最高总价格为\(24\)元（\(=9+8+7\)）。若商品数量是连续的，如图30(b)所示，消费者的总支付意愿为需求曲线下的面积，称为总支付意愿或总用值，代表在给定商品数量下，消费者可以获得的总价值或总好处（Value To Buyers，VTB）。

令\(p=f(q^d)\)为反需求函数，则：

\[VTB = \int_0^q f(q^d)dq\]

(a) 消费者对某种商品的需求曲线 — Fig. 30 需求曲线上的价格为消费者的边际支付意愿。#

(b) 当数量为3单位时，消费者的总支付意愿。 — Fig. 30 需求曲线上的价格为消费者的边际支付意愿。#

消费者盈余的定义#

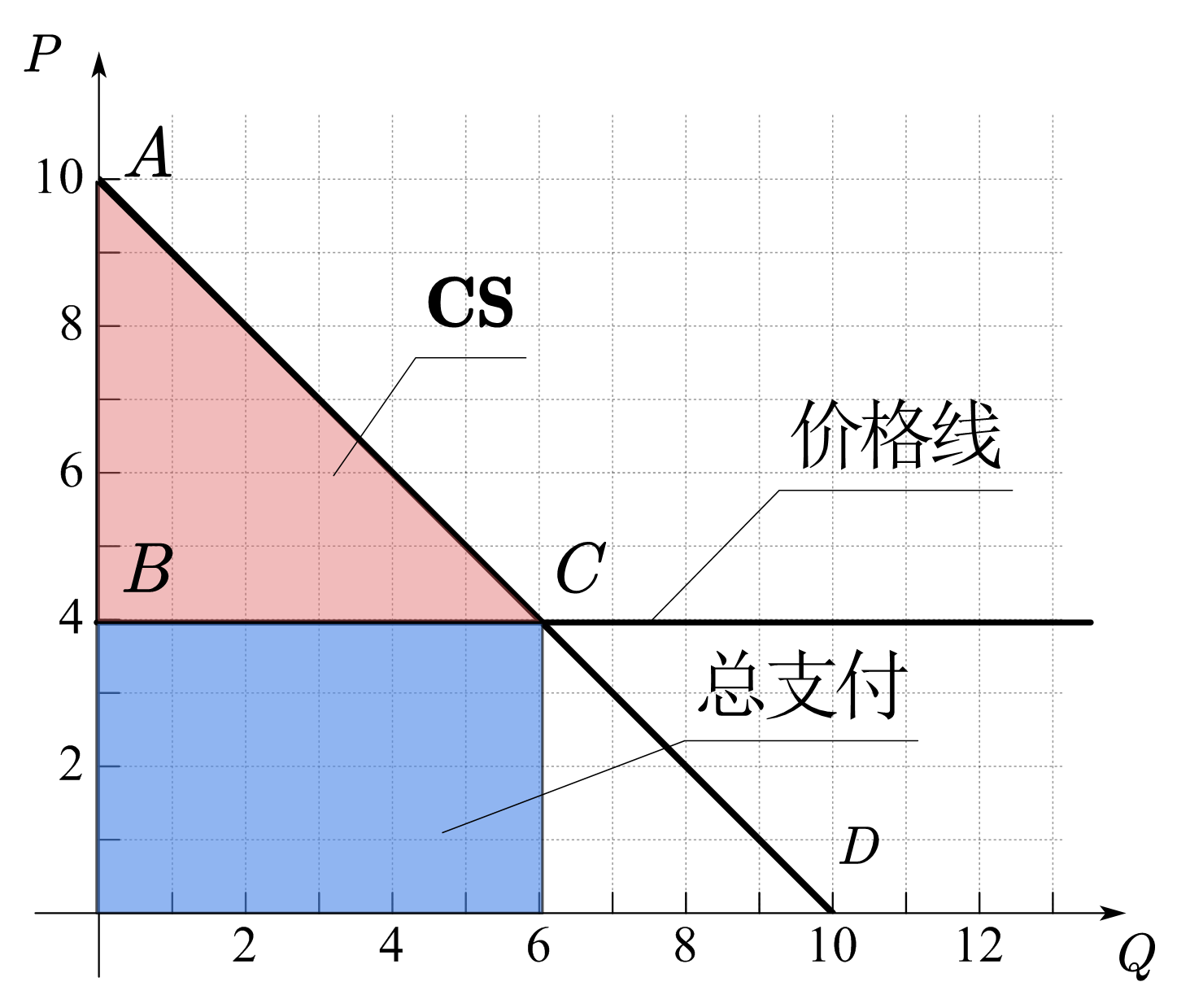
给定商品数量，消费者愿意支付的总价格与实际支付的总价格之差即为其在市场交易中获得的净好处，称为消费者盈余（CS）。

如图31(a)所示，当商品的单价为4元时, 需求量为6单位，价格线下的面积为消费者实际支付的总价格（\(24=6*4\)）。所以消费者盈余为需求曲线之下，价格线之上的面积。图中需求曲线为一条直线，那么消费者盈余等于三角形ABC的面积（\(\frac{1}{2}(10-4)*6=18\)）。如果需求曲线为曲线，那么消费者盈余的计算公式为：

\[ CS = VTB(q) - pq = \int_0^{q} f(q^d)dq^d - pq, \quad p = f(q^d) \]

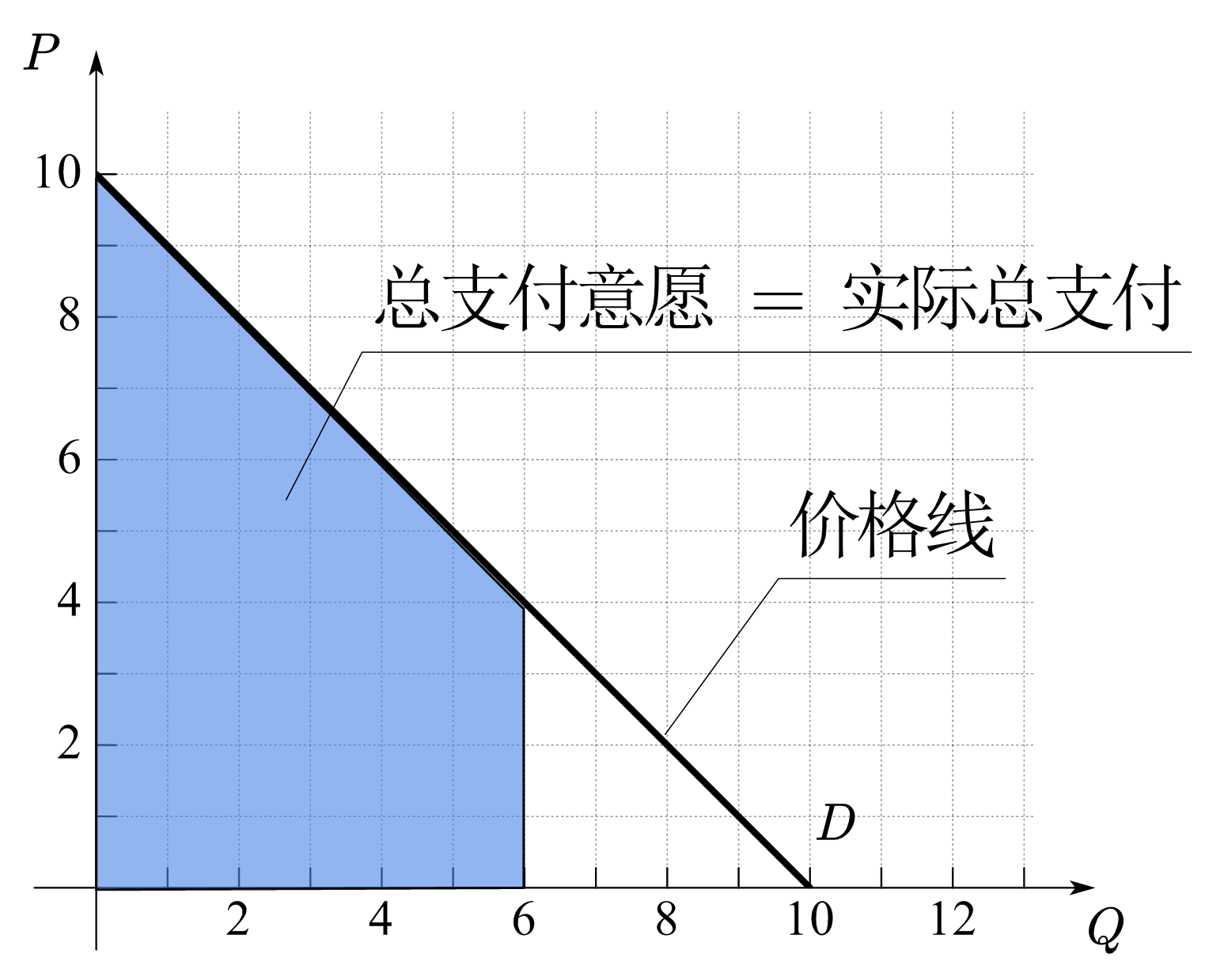
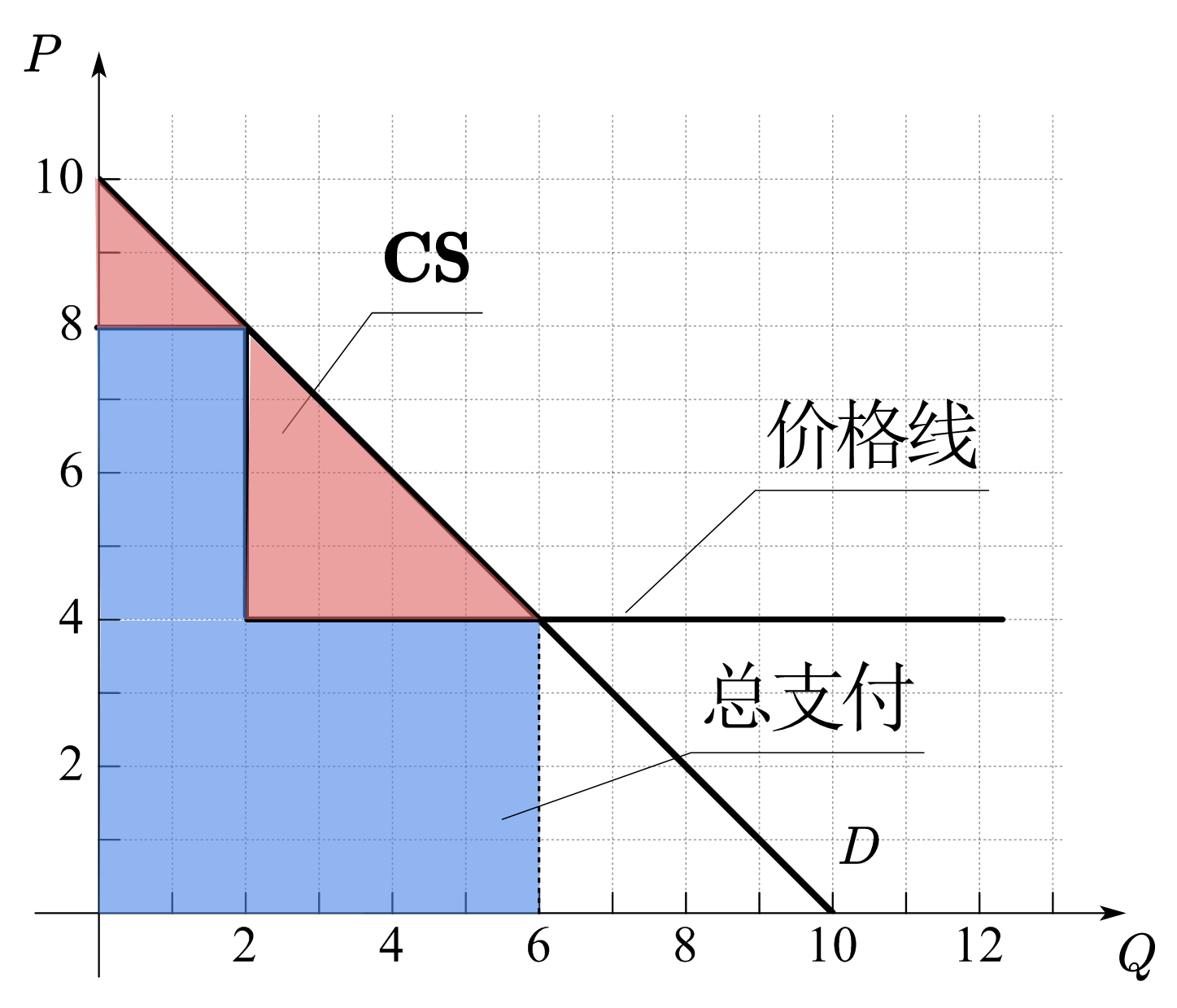
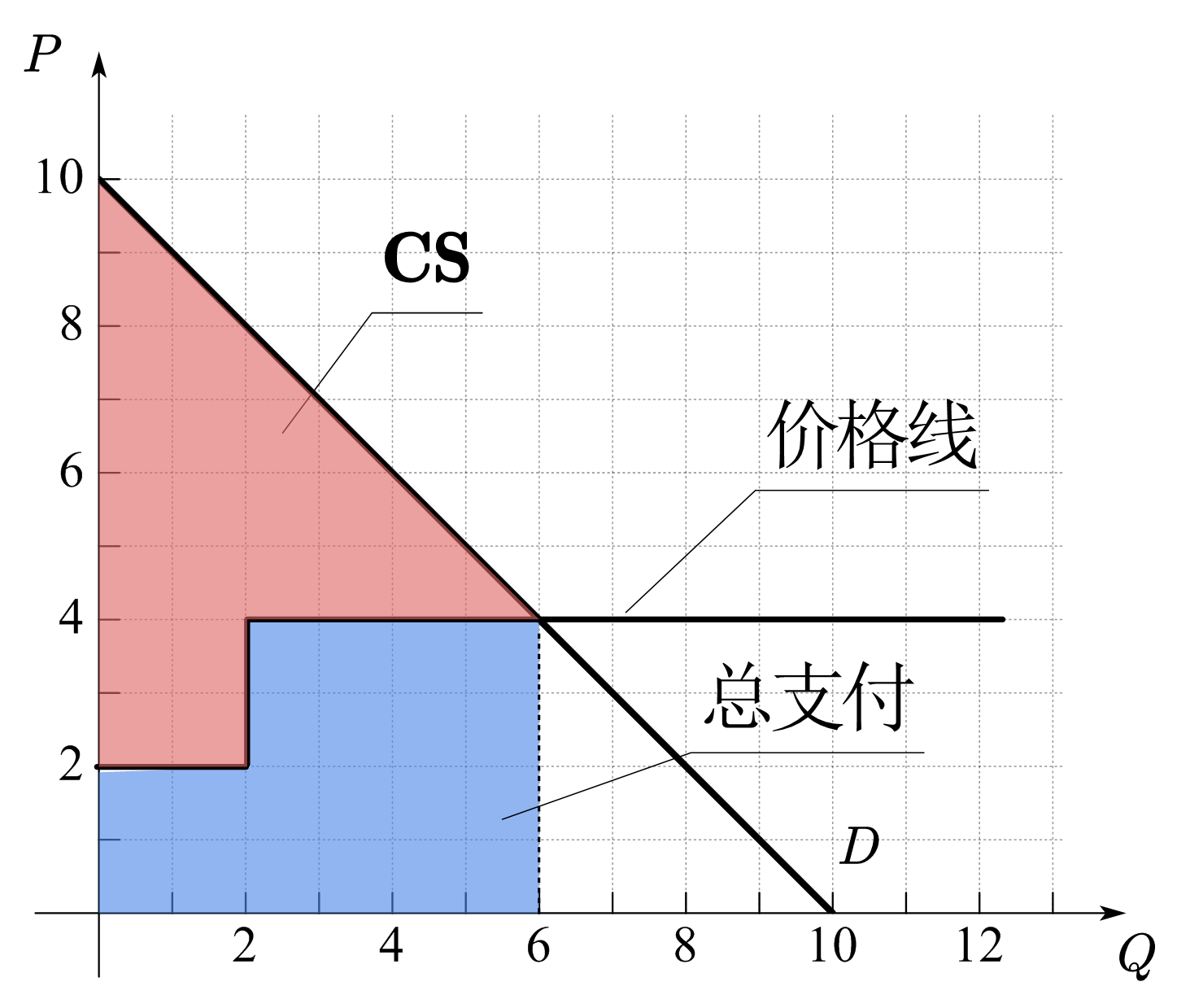
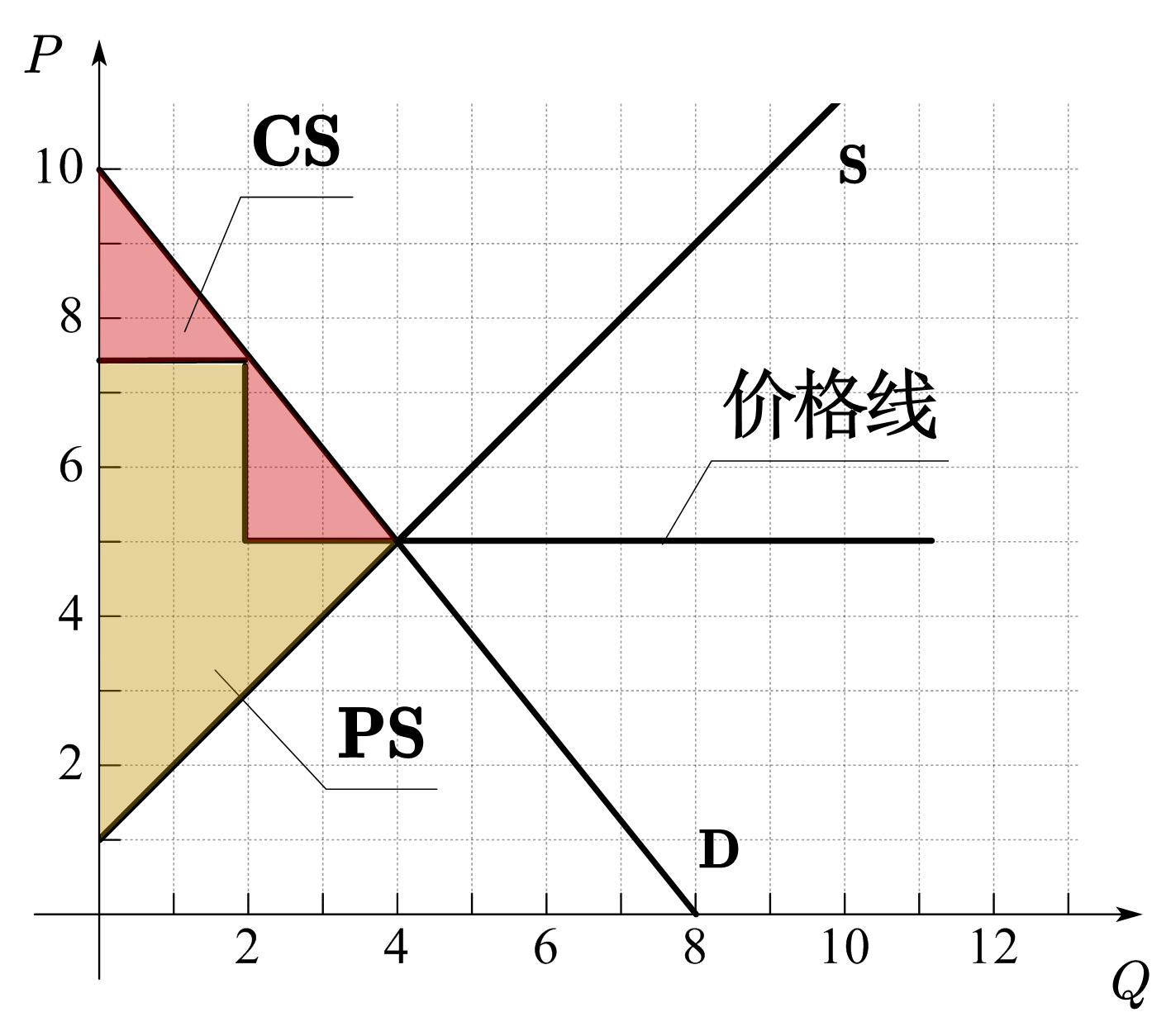
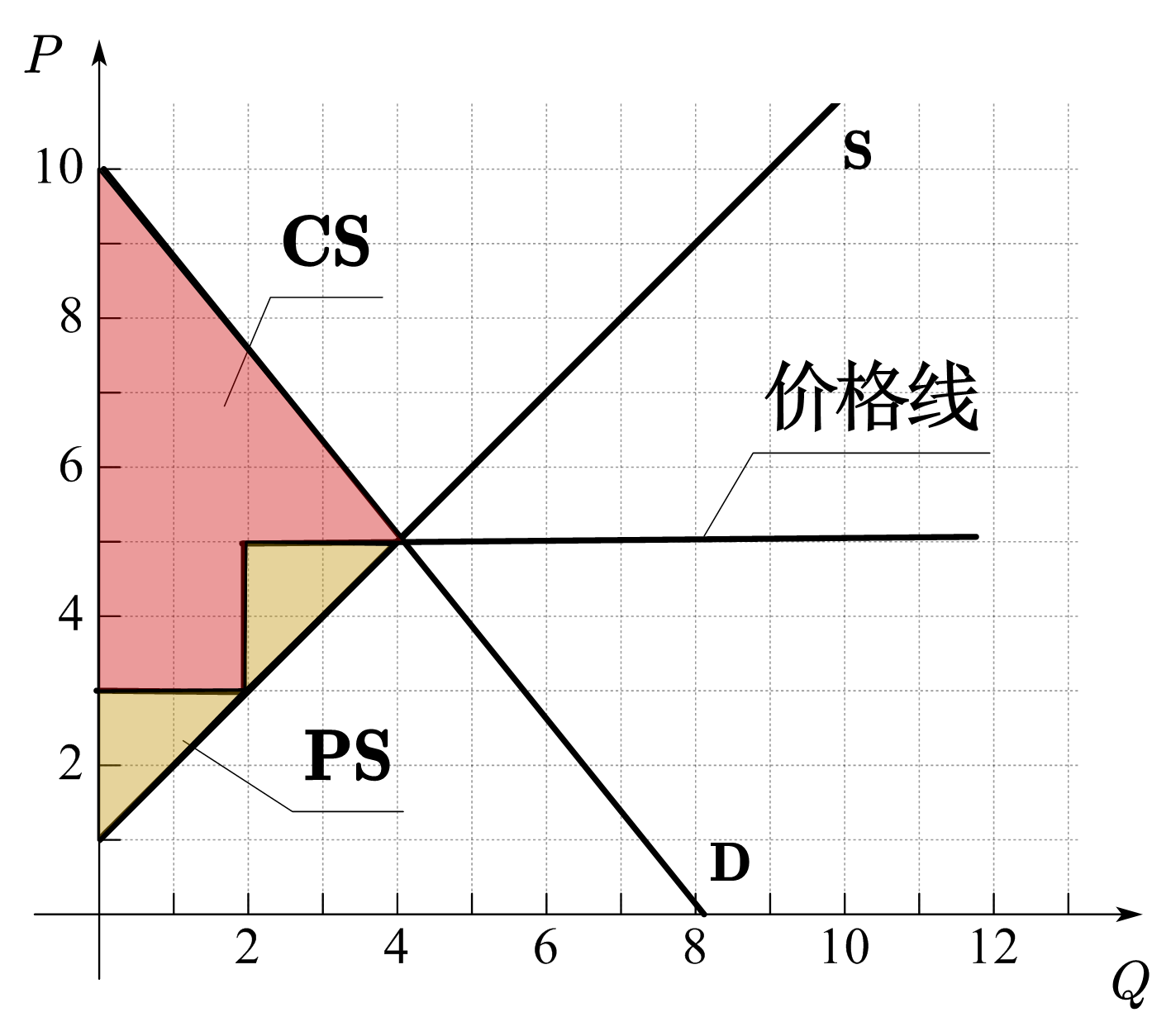
在上述CS的计算中，暗含的商品定价方式为单一定价，即所有商品的售价相同。在现实中，卖方可以有不同的定价方式，在不同的定价方式下，因为支付的总价格不同，所以相同数量下的消费者盈余也会相应的发生变化。图31(b)-(d)画出了其它定价方式下的消费者盈余。图(b)为沿着需求曲线的定价方式，即每单位商品的定价等于消费者的边际支付意愿，如第一单位商品的价格为9元，第二单位为8元，第三单位为7元。这时商品的价格线和需求曲线重合，消费者盈余为0。图(c)是「下台阶」的定价方式，也称为分批定价，即在同一批次内的商品的价格相同，并且价格逐批下降，这时，CS为图中红色区域的面积。图(d)为「上台阶」的定价方式，与「下台阶」的不同之处在于价格逐批上升，CS为图中红色区域的面积。

生产者盈余（Producer Surplus）#

供给曲线上的价格#

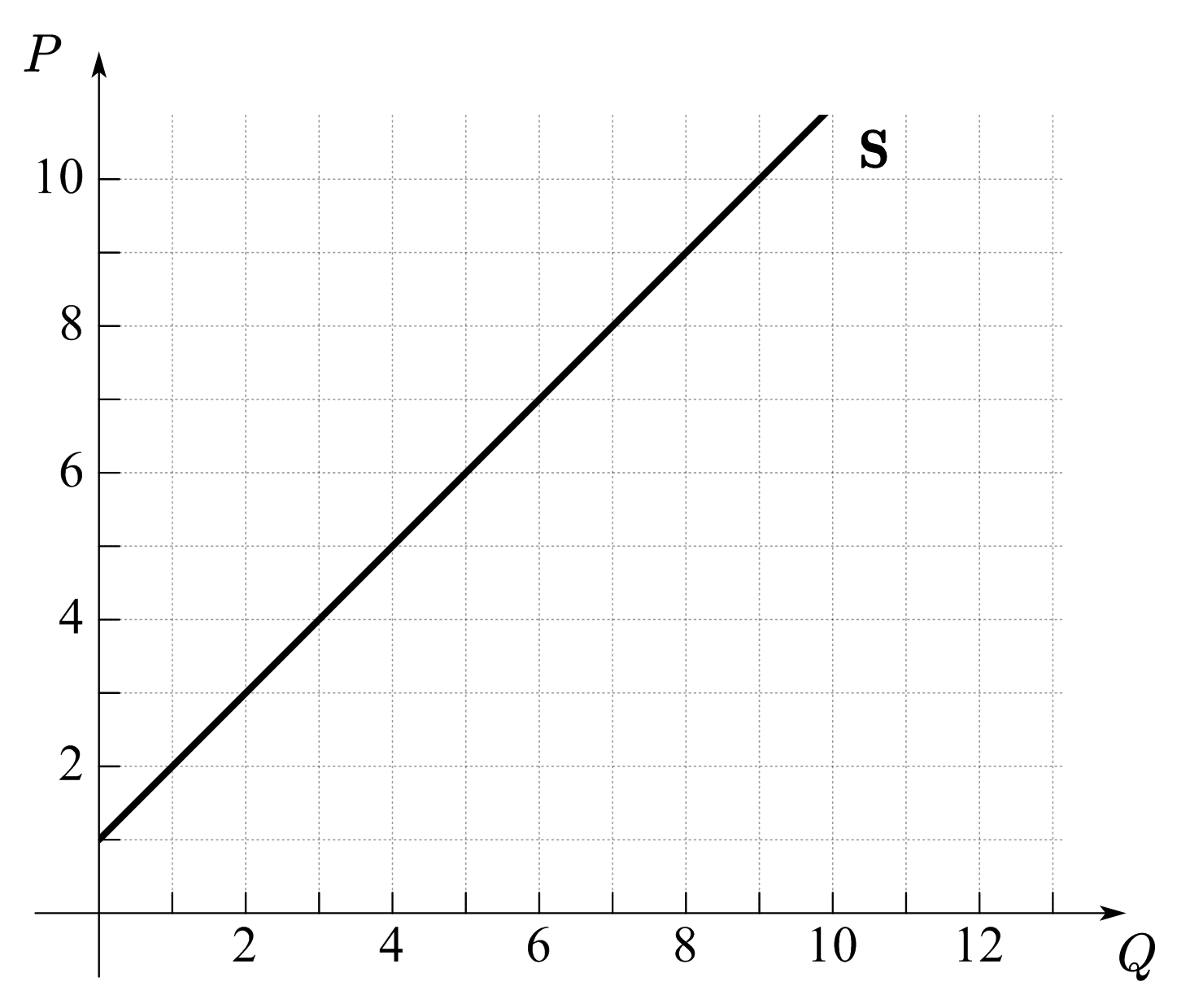
供给曲线是供给关系的几何表示，代表了在不同价格水平下，生产者愿意且能够出售的最大数量。如图32(a)所示，当商品价格为2元，生产者最多愿意出售1单位商品。在出售了1单位商品后，只有当商品价格上升到3元时，生产者才会愿意再出售一单位商品（总计2单位）。同理，在出售了2单位商品后，只有当商品价格上升到4元时，生产者才会愿意再增加一单位商品的出售（总计3单位）。

因此，从增加单位出售的角度看，我们可以将供给曲线上的价格理解为卖方增加一单位商品出售所要求的最低价格。图32(a)中的供给曲线也可以理解为，生产者对第一单位商品的最低售价为2元；由1单位增加至2单位时，最低售价为3元；由2单位增加至3单位时，最低售价为4元，依次类推。因为卖方的售价不会低于商品的成本，所以供给曲线上的价格可以理解为卖方的边际成本。

在经济学中，成本被定义为因选择放弃的最高代价，即为机会成本。我们这里先简单理解一下，为什么供给曲线上的价格代表的是边际成本。在没有生产的情况下，供给曲线和需求曲线本质是一条曲线，因此，需求曲线上的边际用值即代表了放弃这一单位商品的最高代价，即为边际成本。

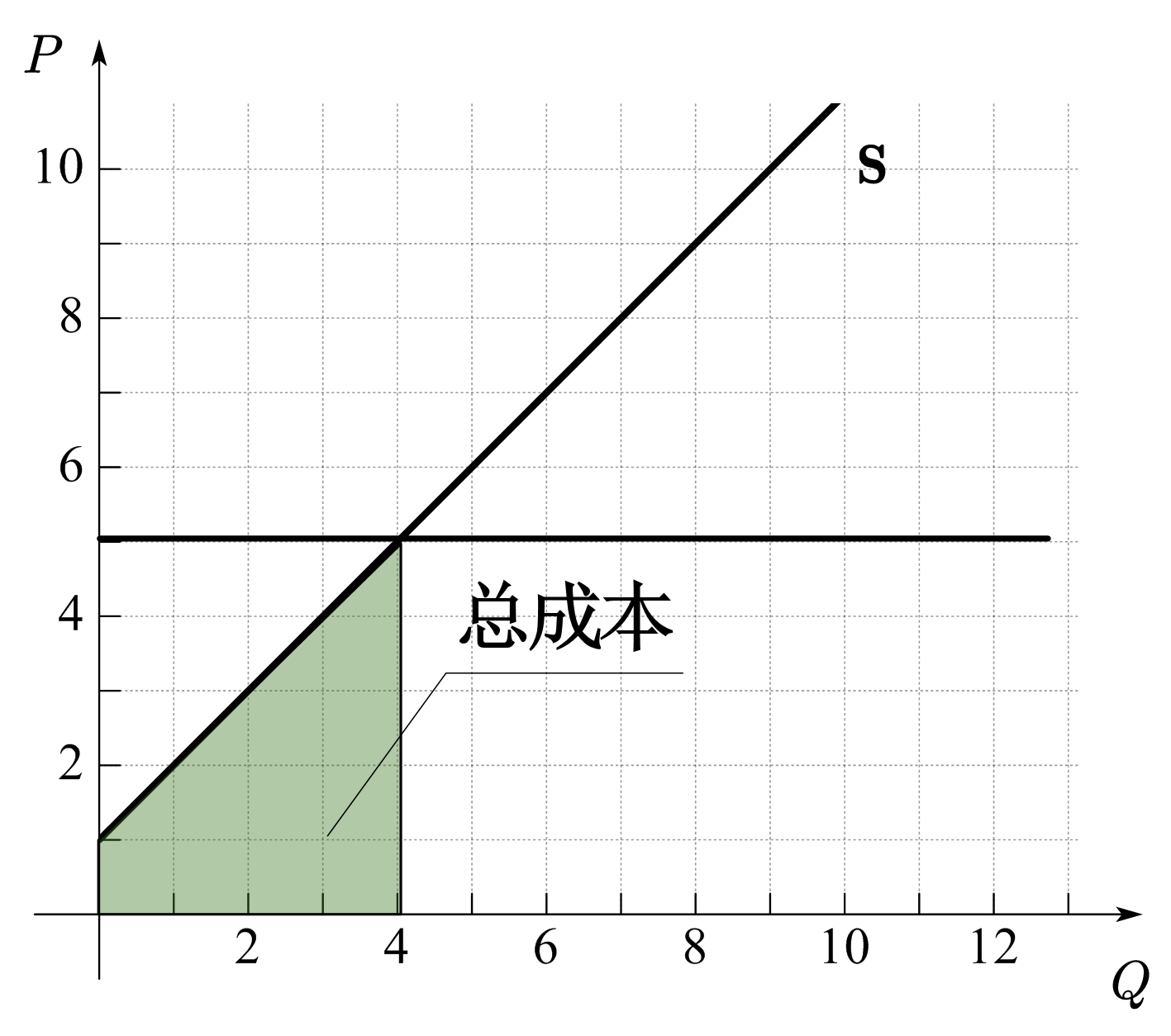
给定商品数量，生产者所要求的最低总价格为边际成本的加总，在图32(b)中，若生产者想出售4单位商品，其所要求的最低总价格为\(14\)元（\(=2+3+4+5\)）。若商品数量是连续的，如图32(a)所示，生产者要求的最低总价格为生产曲线下的面积，代表了出售的总成本（Cost To Sellers, CTS）。

令\(p = g(q^s)\)表示逆供给函数，则

\[ CTS = \int_0^q g(q^s)dq \]

生产者盈余的定义#

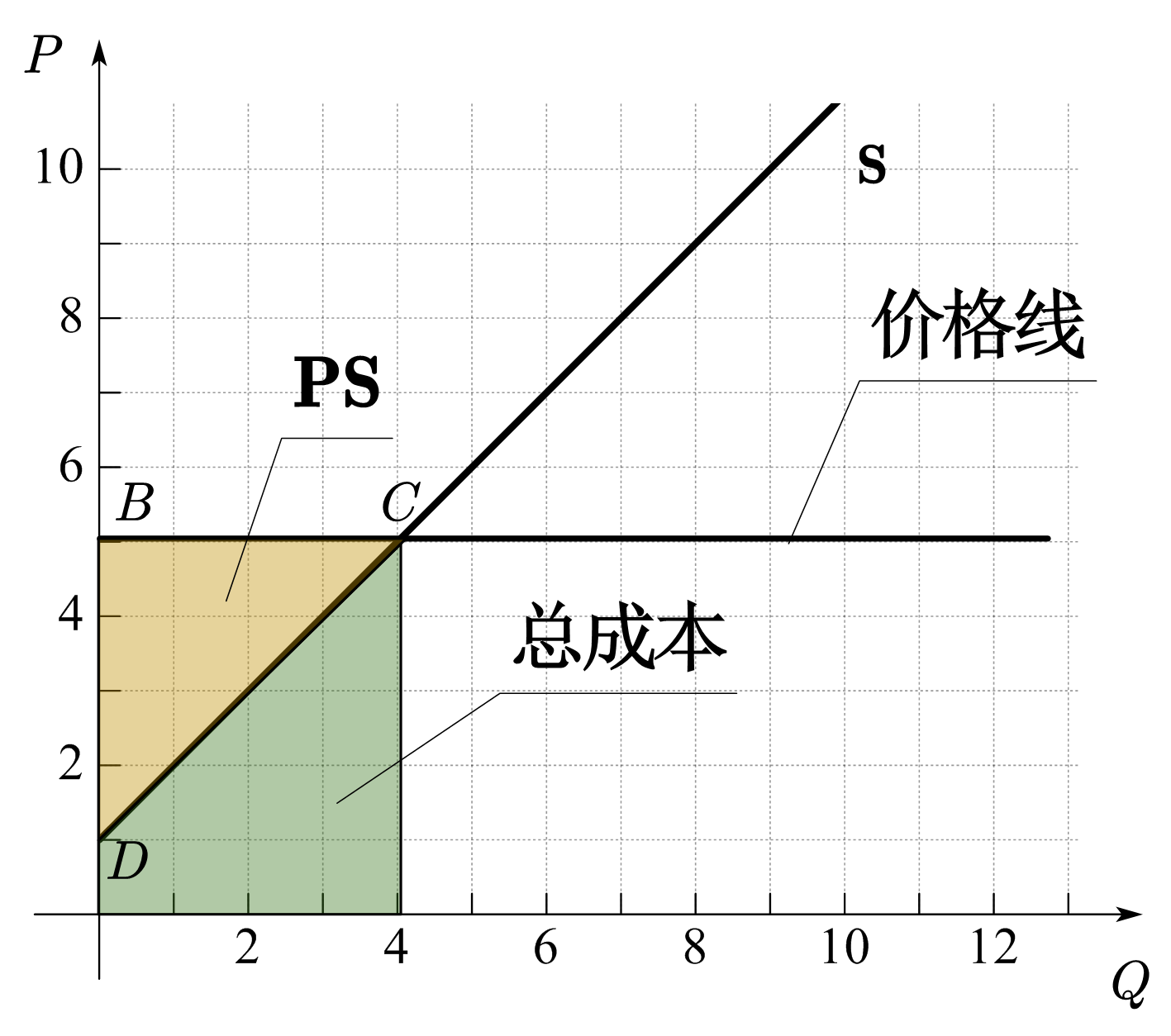
给定商品数量，卖方获得总收入与其所要求的最低总价格之差即为其在市场交易中获得的净好处，称为生产者盈余（PS）。如图33(a)所示，商品的单价为\(p_1\), 给定商品数量\(q_1\)，\(p_1\)价格线下的面积为卖方获得的总价格（\(p_1*q_1\)）。所以，生产者盈余为价格线和供给曲线之间的面积。若供给曲线为一条直线，那么生产者盈余等于三角形DEC的面积（\(\frac{1}{2}(5-1)*4=8\)）。

\[ PS = pq - CTS = pq - \int_0^{q} g(q^s)dq^s, \quad p = g(q^s) \]

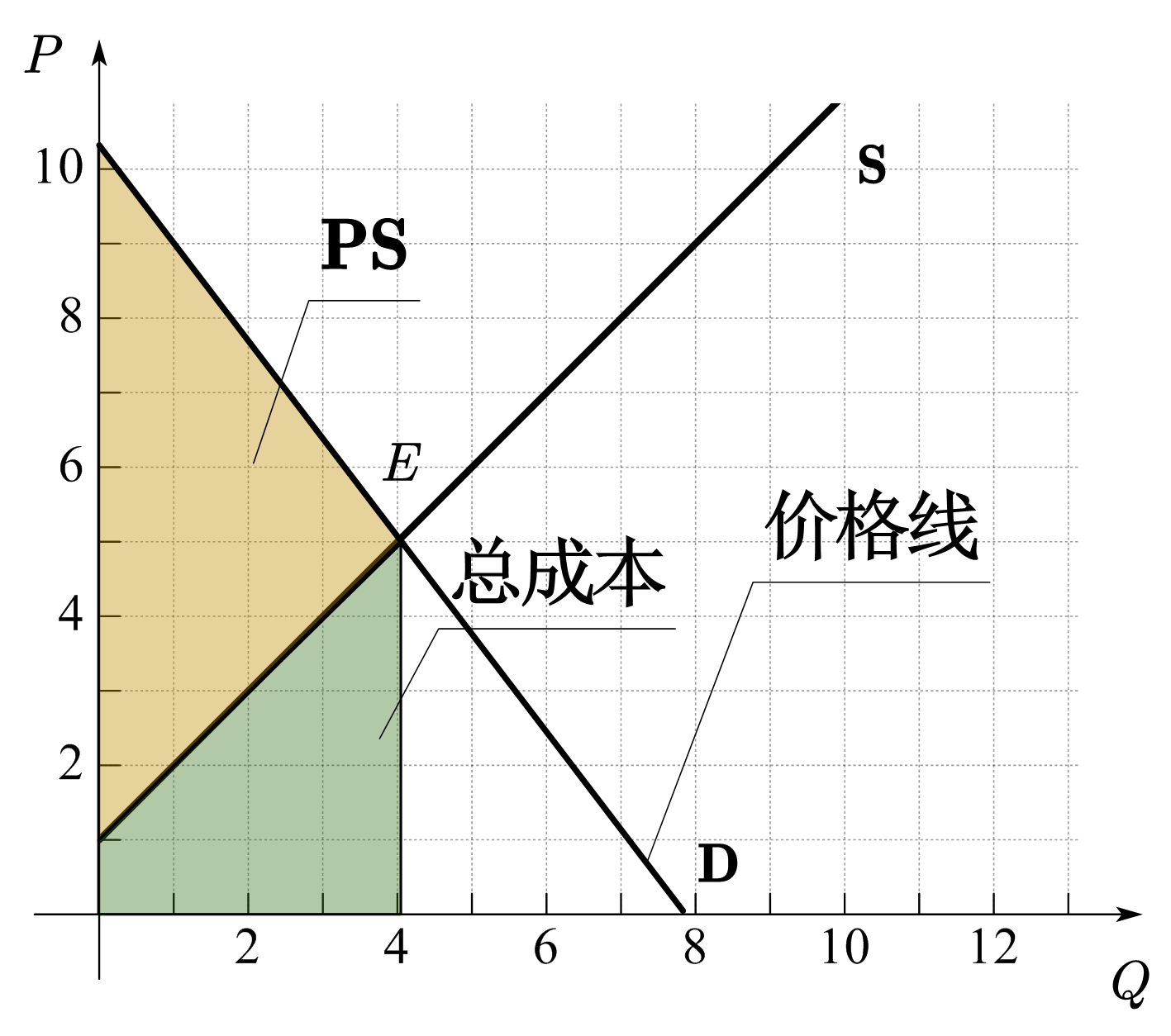
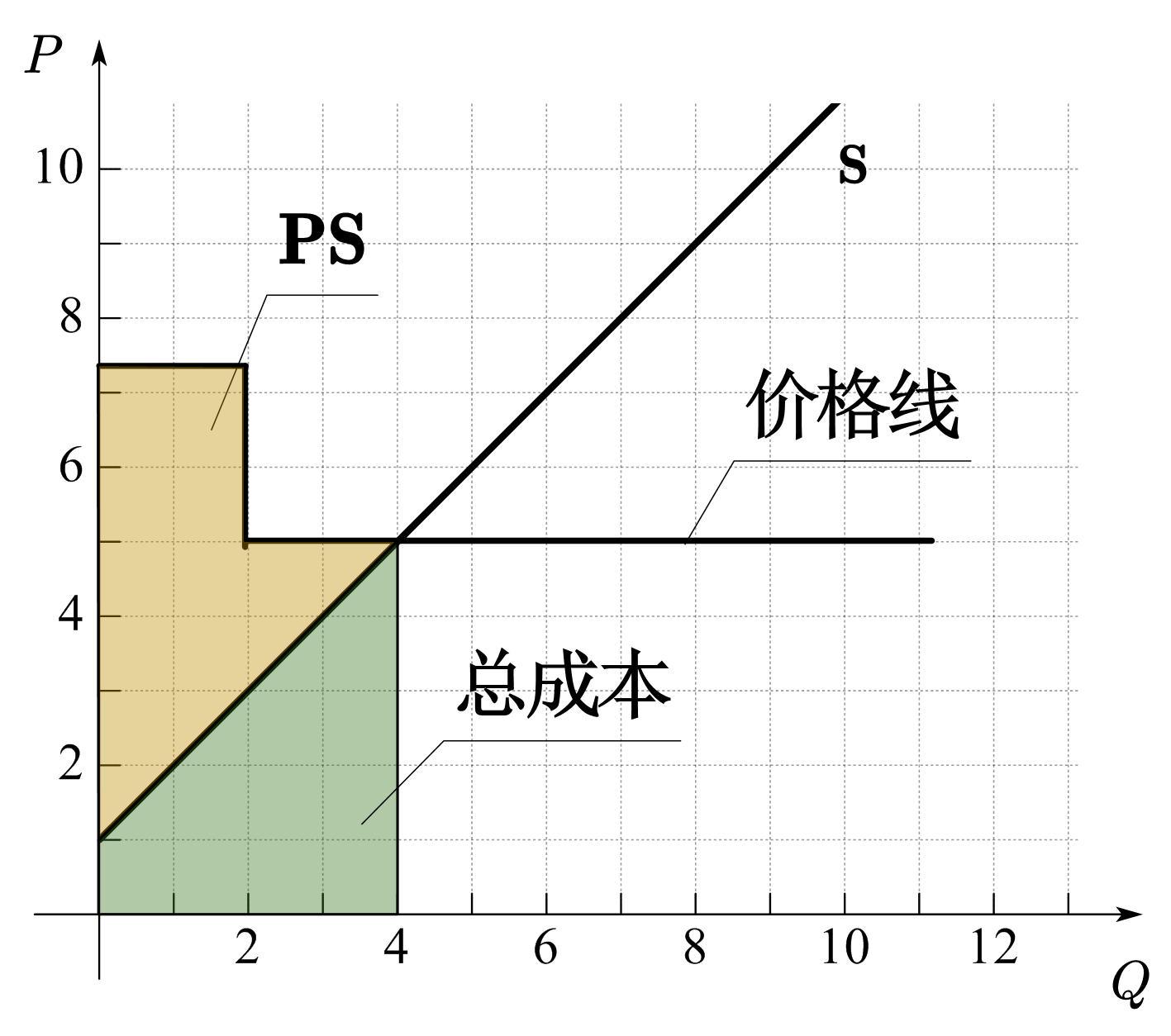
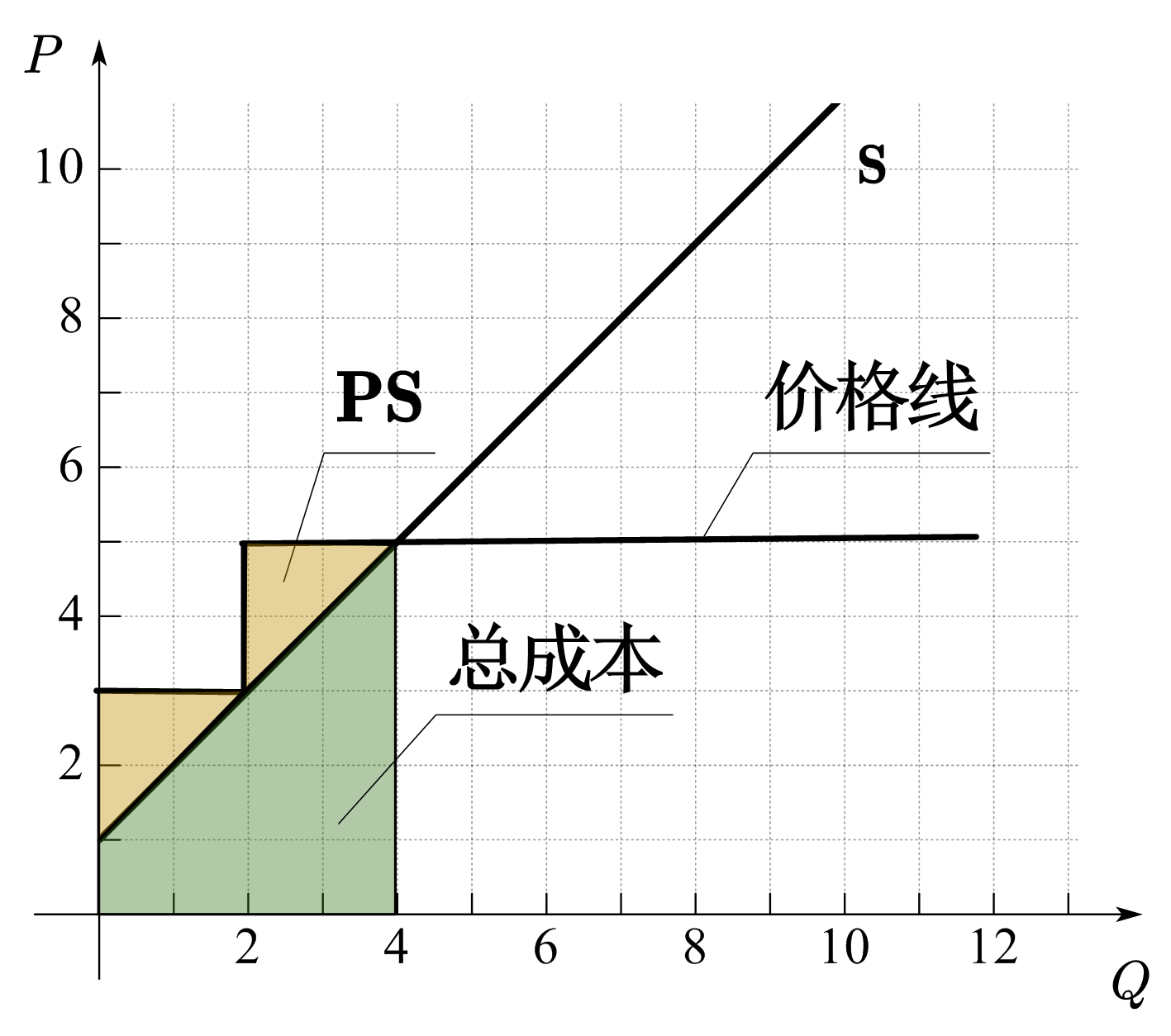
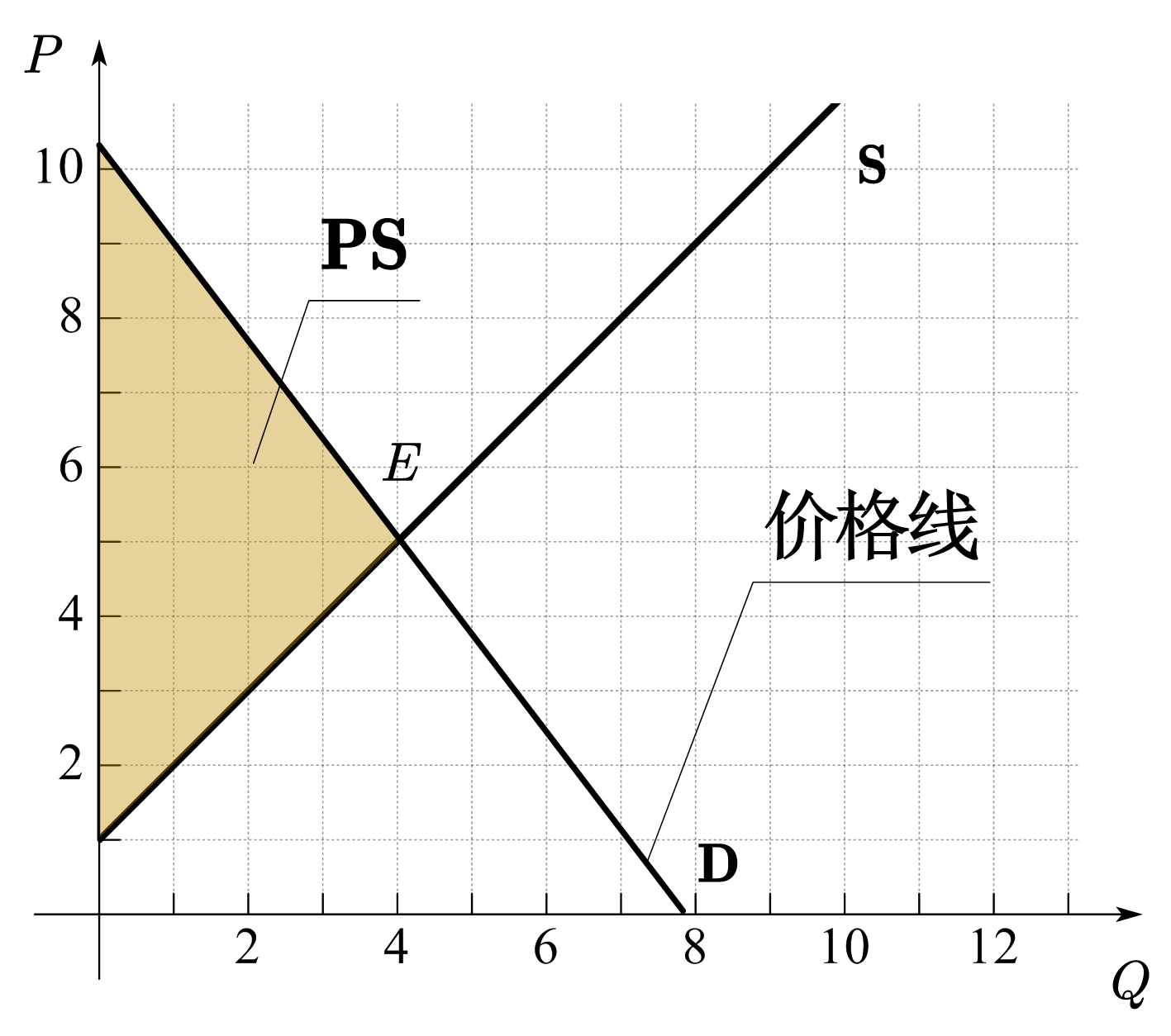
与CS部分分析相同，当卖方的定价方式发生变化时，其获得的总价格会发生变化，所以相同数量下的生产者盈余也会相应的发生变化。图33(b)-(d)展示了其它定价方式下的生产者盈余。图(b)为沿着需求曲线的定价方式，即每单位商品的定价等于消费者的边际支付意愿。因为商品的价格线和需求曲线重合，所以生产者盈余为需求曲线与供给曲线之间的面积，这时没有任何消费者盈余可言。图（c）是「下台阶」的定价方式，这时，PS为图中黄色区域面积。图(d)为「上台阶」的定价方式，PS为图中黄色区域面积。

社会总盈余#

我们将CS与PS之和称为社会总盈余（Total Surplus，TS），代表的是给定商品数量下，买方的总用值与卖方的总成本之差。

CS = 买方总用值 - 买方支付的总价格
PS = 卖方的总收入 - 卖方的总成本
TS = CS + PS = （买方总用值 - 买方支付的总价格） - （卖方的总收入 - 卖方的总成本）= 买方总用值 – 卖方总成本

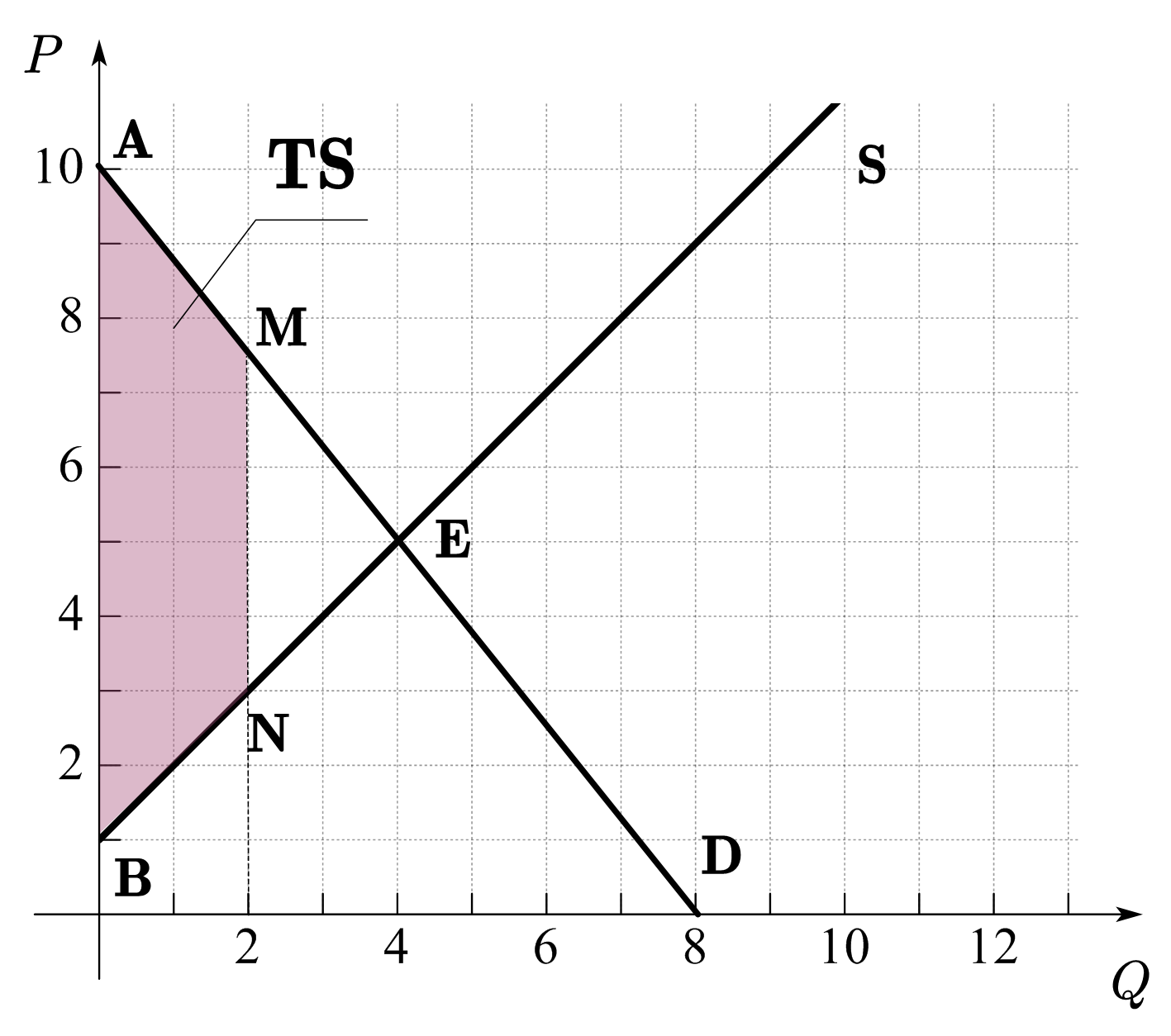
显然，总盈余对应的是需求曲线与供给曲线之间的面积，与商品的定价方式无关，如图34所示，在不同的定价方式下，CS与PS之和都是一样的，不同的定价方式改变的只是盈余在买卖双方的分配。

福利经济学将最大化社会总盈余的产出称为是有效率的，相应的，不能最大化社会总盈余的产出是无效率的。效率是对资源配置的价值判断，可以用于评价不同的资源配置结果。在这个评价标准里，我们不考虑分配是否公平的问题。

最大化社会总盈余的问题也可以称为Social planners’ problem，即存在一个无所不知的社会计划者，可以做出最优的资产配置决策。

Social Planners’ Problem

\[ \max_q \quad TS = CS + PS \]

有效率的产出为：\(q^* = argmax(TS)\)

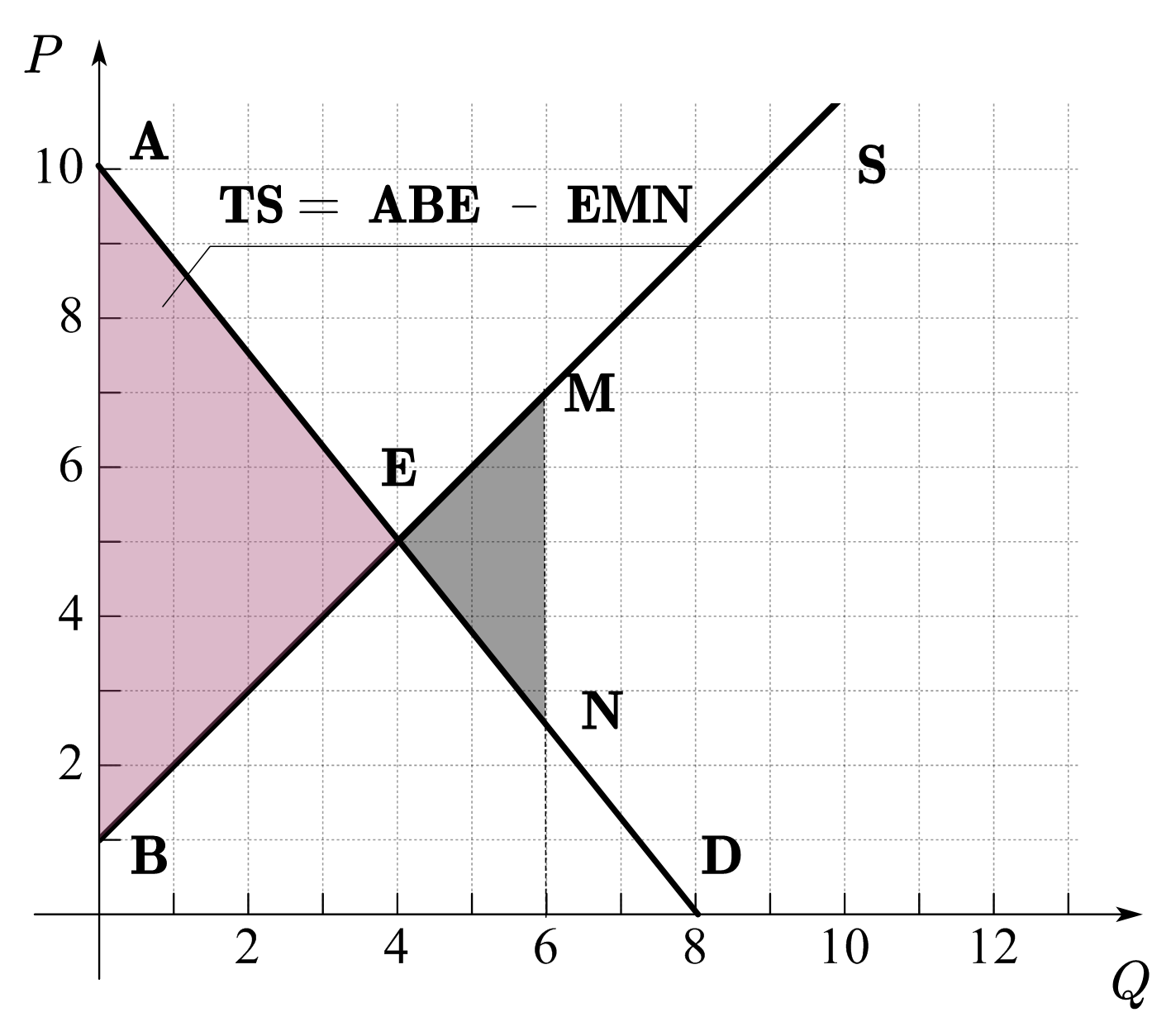
需求曲线上的价格是买方的边际支付意愿或边际用值，可以理解为使用商品的边际收益，供给曲线上的价格是卖方提供商品的边际成本，因此，从社会角度看，供需曲线的交点满足边际收益等于边际成本，恰为我们之前所讲的最优条件。这说明，在没有政府干预的条件下，供需交点所对应的均衡产量是最大化社会总盈余的产量，即市场的均衡产量是有效率的。如图35所示，当产量不等于均衡数量时，社会总盈余都会下降。该结论通常被用作支持市场的理由。

(a) 产量低于均衡产量 — Fig. 35 当产量不等于均衡产量时，社会总盈余会下降。#

(b) 产量高于均衡产量 — Fig. 35 当产量不等于均衡产量时，社会总盈余会下降。#

Laissez faire (French for “allow them to do”)#: The notion that government should not interfere with the market. Government cannot raise total surplus by changing the market’s allocation of resources.

check

一般均衡模型

前提假设：没有交易费用
该价格的逻辑问题在于：如果没有交易费用，我们不需要使用市场。
此外，需要注意的是，没有考虑使用市场的成本。

帕累托最优和帕累托改进#